Question

A particle moves along a curve of unknown shape, but magnitude of force F is constant and always acts along a tangent to the curve. Then
(A) $\overrightarrow F $ may be conservative
(B) $\overrightarrow F $ must be conservative
(C) $\overrightarrow F $ may be non-conservative
(D) $\overrightarrow F $ must be non-conservative

Answer 1

Hint: We know that conservative force is path independent and non-conservative forces are path dependent. We must observe the work done by F along a curve to know the nature of the force.

Complete step by step answer We can consider a path and see how much work done if an applied force makes some displacement

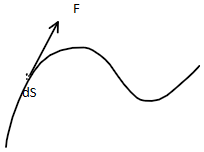
As you can see in the diagram, a curve of unknown shape has force F acting along the tangent and is constant, so for small displacement dS,
Hence work done $W = \int\limits_0^S {\overrightarrow F d\overrightarrow S } = \int\limits_0^S {FdS\cos \theta } $ since F is constant.
$ \Rightarrow W = F\int\limits_0^S {dS} $so, the work done by force F is dependent on path
From the question we can see that the work done at every point of curve is dependent upon the path followed. If the work done is conservative in nature then, the force acting must be non-conservative.

Hence, option D. $\overrightarrow F $ must be non-conservative.

Additional information
Work done by a conservative force is recoverable and if within a system only conservative force acts then the system's kinetic and potential energy can change. It must be noted that the mechanical energy (that is the sum of kinetic and potential energy) remains the same. Some examples are magnetic force, elastic force, gravitational force, electrostatic force and so on. However, work done by non-conservative forces may lead to dissipation of energy in the form of heat energy and it is not recoverable completely. Examples are air resistance, viscous forces.

Note:
Conservative forces are central in nature. It means that these forces act along the line connecting the centers of the bodies like for example electrostatic and gravitational forces. Non-conservative forces are generally velocity dependent and have retarding nature.