Question

When a particle is moving in vertical circle,
A) Its radial and tangential acceleration both are constant
B) Its radial and tangential acceleration both are varying
C) Its radial acceleration is constant but tangential acceleration is varying
D) Its radial acceleration is varying but tangential acceleration is constant

Answer 1

Hint: To this thing we assume a particle which is moving in vertical circular path when any object moving in vertical circular path then it has both type of acceleration radial acceleration as well as tangential acceleration by the radial acceleration object change its direction regularly means it helps to maintain the motion in a circular path Which provided by the centripetal Force and tangential acceleration act along in tangential direction which manage the speed of object in path

Complete step by step solution:
Whenever object move in a vertical circular path then it has both type of acceleration
Let us assume the object of mass Moving in a vertical circular path with the help of a string when it moved in circular path centripetal force acts on it to maintain its circular path

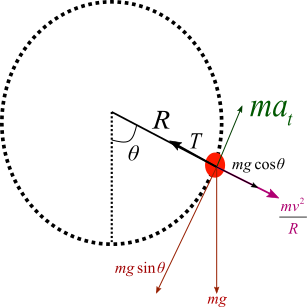
As you can see in the diagram at any instant the object at point B at this moment the force on the object mentioned in the above diagram.
From this diagram we can write following equations
Balancing force in radial direction
$ \Rightarrow mg\cos \theta + \dfrac{{m{v^2}}}{R} = T$
$ \Rightarrow \dfrac{{m{v^2}}}{R} = T - mg\cos \theta $
Here $\dfrac{{{v^2}}}{R}$ Is the centripetal acceleration toward the centre which is also known as radial acceleration ${a_R}$
From above equation Radial acceleration${a_R}$
$\therefore {a_R} = \dfrac{{T - mg\cos \theta }}{m}$ ................... (1)
From this equation we can see that radial acceleration depends upon angle $\theta $ which is varying so radial acceleration varies in vertical circular motion.
For tangential force
$ \Rightarrow m{a_t} = mg\sin \theta $
So tangential acceleration ${a_t}$
$\therefore {a_t} = g\sin \theta $
So we can see from this equation tangential acceleration also depends upon angle $\theta $ so tangential acceleration is also varying in vertical circular motion.

Hence option B is correct.

Note: We know best speed of object moving in vertical circular path gradually decreases when it move from lowest most point to the top most point and the speed of object gradually increases when object move top most point to the lowermost point it means the magnitude off velocity of object continuously change in vertical motion.