Question

A particle at rest suddenly disintegrates into two particles of equal masses which starts moving. The two fragments will:
A. Move opposite with unequal speeds
B. Move in any direction with any speed
C. Move in same direction with equal speed
D. Move opposite with equal speed

Answer 1

Hint: Recall that law of conservation of momentum that suggests that the initial and final momenta of a system are equal, which means that the momentum of a system remains constant throughout time. Now, since the particle is initially at rest the initial momentum will be zero.
Now, calculate an expression for the final momentum of the system by summing the individual particle momenta and equate it to the zero initial momentum and get the relation between the velocities of the two particles. This will give you the required answer.

Formula used:
Law of conservation of momentum: $p_{i} = p_{f}$, where $p_i$ is the initial momentum of a system and $p_f$ is the final momentum of the system.

Complete answer:
To work on this question, we make use of the Law of Conservation of Momentum.
According to this law, the total momentum of an isolated system remains constant, which means that the momentum of the system is conserved at any time. This suggests that there is no creation or destruction of momentum and in any case, there is only a transfer of momentum within the constituents of this system.
Thus, this law tells us that the initial and final momenta of the system are equal.
Now let us look at the situation given to us.

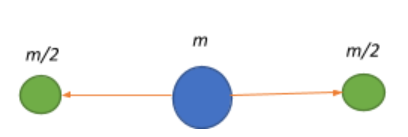
We first have a particle of say, mass m that is at rest.
Therefore, the initial momentum of the system $\vec{p_i} = m(0) = 0\;kgms^{-1}$
Now, this particle disintegrates into two particles of equal masses that start moving. This means that $m_1 = m_2 = \dfrac{m}{2}$, and let them move with a velocity $\vec{v_1}$ and $\vec{v_2}$ respectively.
Therefore, the final momentum of this system $\vec{p_f} = \dfrac{m}{2}\vec{v_1} + \dfrac{m}{2}\vec{v_2}$
From the law of conservation of momentum, we have:
$\vec{p_i} = \vec{p_f}$
$\Rightarrow 0 = \dfrac{m}{2}\vec{v_1} + \dfrac{m}{2}\vec{v_2} \Rightarrow 0 = \dfrac{m}{2}(\vec{v_1} +\vec{v_2})$
$\Rightarrow 0 = \vec{v_1} + \vec{v_2} \Rightarrow \vec{v_1} = -\vec{v_2}$
This means that both the particles move with the same speed after disintegration but move in opposite directions, as is indicative from the negative sign of the velocity vector.
Thus, the correct option would be D. Move opposite with equal speed.

Note: While using vector forms of quantities it becomes highly important to ensure that the signs associated with each vector are verified and accounted for, since represented a quantity as a vector implies that we are taking into consideration the directional information that it provides in addition to its magnitude, and any inconsistency in the signs will result in a wrongly oriented vector, which is not the result we want to get.