Question

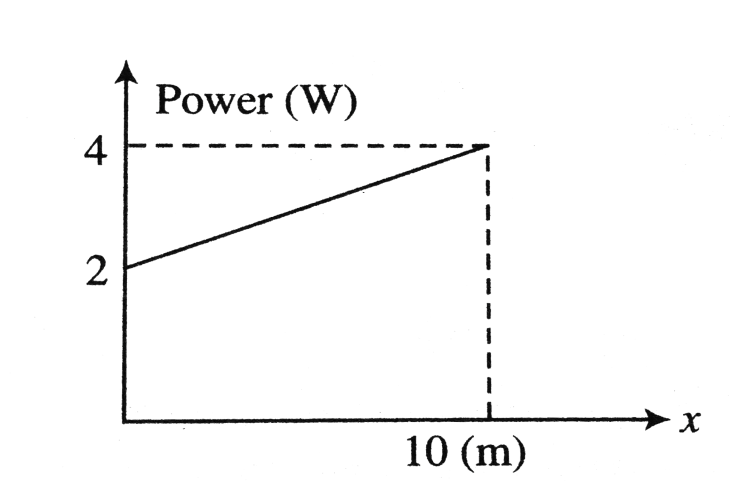
A particle A of mass $\dfrac{{10}}{7}kg$ is moving in the positive direction of $x$ . At initial position $x = 0$ its velocity is $1m/s$ , then its velocity at $x = 10m$ is: (use the graph given)

A) $4m/s$
B) $2m/s$
C) $3\sqrt 2 m/s$
D) $\dfrac{{100}}{3}m/s$

Answer 1

Hint: First, we will derive the relation between force and distance by using the relation between Power force and Velocity and the equate the area under the graph with the derived formula to get the final answer.

Formula used:
Power, $P = F \times v$
Where, $F$ is the force and $v$ is the velocity
Area of trapezium, $A = \dfrac{1}{2}(a + b) \times h$
Where, $a,b$ are the lengths of the parallel sides of trapezium and $h$ is the height of the trapezium.

Complete step by step solution:
As we know, Power, $P = F \times v$
Where, $F$ is the force and $v$ is the velocity
Also, $F = ma$ $ \Rightarrow P = ma \times v$
Since $a$ is the derivative of $v$ , and $v$ is the derivative of $m$ ,
$P = m\dfrac{{dv}}{{dt}} \times v \Rightarrow P = m\dfrac{{dv}}{{dx}}\dfrac{{dx}}{{dt}} \times v$
$ \Rightarrow P.dx = mvdv\dfrac{{dx}}{{dt}}$
Which gives, $P.dx = m{v^2}dv$ (since $\dfrac{{dx}}{{dt}} = v$ )
Integrating both sides,
$\int {P.dx = \int\limits_1^v {m{v^2}dv} } $
$ \Rightarrow P = [\dfrac{{m{v^3}}}{3}]_1^v$
Which gives, $P = \dfrac{m}{3}({v^3} - 1)$
Now we have mass equal to $\dfrac{{10}}{7}kg$
Also, the area under a curve between two points can be found by doing a definite integral between the two points. Here that area is present in the shape of trapezium. A trapezium is a $2D$ shape and a type of quadrilateral, which has only two parallel sides and the other two sides are non-parallel.
Therefore, Area of trapezium, $A = \dfrac{1}{2}(a + b) \times h$
Where, $a,b$ are the lengths of the parallel sides of trapezium and $h$ is the height of the trapezium.
$ \Rightarrow A = \dfrac{1}{2}(2 + 4) \times 10 = \dfrac{1}{2} \times 6 \times 10 = 30$
We derived a relation between power and distance. Equate both the values
$ \Rightarrow \dfrac{m}{3}({v^3} - 1) = 30$
$ \Rightarrow \dfrac{{10}}{{7 \times 3}}({v^3} - 1) = 30$
This gives, $v = 4m/s$

Hence, Option (A) is correct.

Note: Convert all the given values into SI units before using them in any question. Don’t forget to put units in the final answer. We had to derive a relation between Power and Mass because in the question, the graph is given in terms of Power and mass only.