Question

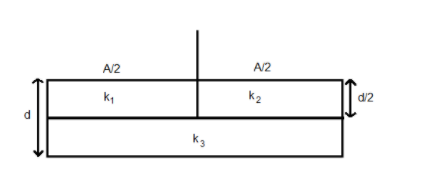
A parallel capacitor of area A, plate separation d, and capacitance C is filled with three dielectric materials having dielectric constants ${{k}_{1}}$, ${{k}_{2}}$ and ${{k}_{3}}$ as shown. If a single dielectric material is to be used to have the same capacitance in the capacitor, then its dielectric constant k is given by

$\text{A}\text{. }k\text{ }=\text{ }{{k}_{1}}+{{k}_{2}}+{{k}_{3}}$
$\text{B}\text{. }k\text{ }=\text{ }\dfrac{{{k}_{1}}{{k}_{2}}}{{{k}_{1}}+\text{ }{{k}_{2}}}+\text{ }2{{k}_{3}}$
$\text{C}\text{. }\dfrac{1}{k}\text{ }=\text{ }\dfrac{1}{{{k}_{1}}}+\dfrac{1}{{{k}_{2}}}+\dfrac{1}{{{k}_{3}}}$
$\text{D}\text{. }\dfrac{1}{k}\text{ }=\text{ }\dfrac{1}{{{k}_{1}}+{{k}_{2}}}+\dfrac{1}{2{{k}_{3}}}$

Answer 1

Hint: When a dielectric medium (material) is inserted in between the parallel plates of capacitance, the capacitor acts as a new capacitor with more capacitance value. i.e. $C'=\dfrac{k{{\varepsilon }_{{}^\circ }}A}{d}=kC$. If there is more than one dielectric material, each dielectric material acts as a separate capacitor. Then we can convert the dielectrics into capacitors, which makes the work easier. Also, use the formulas to find the equivalent capacitance when the capacitors are in series and parallel connection.
Formula used:
$C=\dfrac{{{\varepsilon }_{\circ }}A}{d}$
$C'=\dfrac{k{{\varepsilon }_{{}^\circ }}A}{d}=kC$.
${{C}_{12}}={{C}_{1}}+{{C}_{2}}$
$\dfrac{1}{{{C}_{123}}}=\dfrac{1}{{{C}_{12}}}+\dfrac{1}{{{C}_{3}}}$
Complete step by step answer:
The capacitance of a capacitor is given as $C=\dfrac{{{\varepsilon }_{\circ }}A}{d}$, where C is the capacitance of the capacitor, A is an area of parallel metal plates, d is the perpendicular distance between the two parallel plates and ${{\varepsilon }_{\circ }}$ is the permittivity of the free space. This value of capacitance is when there is air in the space between the plates. If there is another medium, which we call as dielectric then the capacitance of the capacitor changes. Dielectric medium is a poor conducting material that creates an internal electric field when an external electric field acts on it.
To understand the new electric field created between the plates after adding the dielectric material, we have something known as dielectric constant (k). $k=\dfrac{E}{E'}$, where E is the electric field without the dielectric material and E’ is the reduced electric field after inserting the dielectric material. The value of k is always greater than one.
When a dielectric material is inserted in between the parallel plates of the capacitor, the capacitance of the capacitor increases by a factor of K called dielectric constant. Therefore, the new capacitance becomes $C'=\dfrac{k{{\varepsilon }_{\circ }}A}{d}=kC$.
 So the dielectric acts as an updated capacitor in the circuit.
 If you see the given figure, we can divide it into three different capacitors. Let the capacitance with dielectric constants ${{k}_{1}}$, ${{k}_{2}}$ and ${{k}_{3}}$ be ${{C}_{1}}$, ${{C}_{2}}$ and ${{C}_{3}}$ respectively. Let us now write the expression for each capacitance. The width of the capacitor (${{C}_{1}}$) is $\dfrac{d}{2}$ and the area is $\dfrac{A}{2}$, so the capacitance ${{C}_{1}}={{k}_{1}}\dfrac{{{\varepsilon }_{\circ }}\left( \dfrac{A}{2} \right)}{\left( \dfrac{d}{2} \right)}={{k}_{1}}\dfrac{{{\varepsilon }_{\circ }}A}{d}$. ……….(1)
Similarly, the capacitance${{C}_{2}}={{k}_{2}}\dfrac{{{\varepsilon }_{\circ }}\left( \dfrac{A}{2} \right)}{\left( \dfrac{d}{2} \right)}={{k}_{2}}\dfrac{{{\varepsilon }_{\circ }}A}{d}$. ……..(2).
The width of the third capacitor (${{C}_{3}}$) is $\dfrac{d}{2}$ and the area is A. therefore, the capacitance${{C}_{3}}={{k}_{3}}\dfrac{{{\varepsilon }_{\circ }}A}{\left( \dfrac{d}{2} \right)}=2{{k}_{3}}\dfrac{{{\varepsilon }_{\circ }}A}{d}$. ……….(3).
As we can see that the dielectric with electric constants ${{k}_{1}}$ and ${{k}_{2}}$ are in parallel and ${{k}_{3}}$ is in series with${{k}_{1}}$ and ${{k}_{3}}$. Redraw the figure and replace the dielectrics with their respective capacitance as shown. It will be easier to understand.

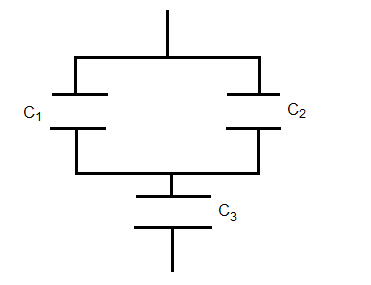
The capacitors ${{C}_{1}}$ and ${{C}_{2}}$ are in parallel. So the effective capacitance (${{C}_{12}}$) of these two will be the sum of the two capacitances.
 $\Rightarrow {{C}_{12}}={{C}_{1}}+{{C}_{2}}$. Substitute the values of ${{C}_{1}}$ and ${{C}_{2}}$ from equations (1) and (2).
Therefore, ${{C}_{12}}={{k}_{1}}\dfrac{{{\varepsilon }_{\circ }}A}{d}+{{k}_{1}}\dfrac{{{\varepsilon }_{\circ }}A}{d}=\left( {{k}_{1}}+{{k}_{2}} \right)\dfrac{{{\varepsilon }_{\circ }}A}{d}$. …….(4)
The capacitor ${{C}_{3}}$ is in series with ${{C}_{12}}$. The reciprocal of the effective capacitance (${{C}_{123}}$) of these two will be the sum of the reciprocals of the individual capacitance i.e. $\dfrac{1}{{{C}_{123}}}=\dfrac{1}{{{C}_{12}}}+\dfrac{1}{{{C}_{3}}}$ . Substitute the values of ${{C}_{12}}$ and ${{C}_{3}}$ from equations (3) and (4).
$\Rightarrow \dfrac{1}{{{C}_{123}}}=\dfrac{1}{\left( {{k}_{1}}+{{k}_{2}} \right)\dfrac{{{\varepsilon }_{\circ }}A}{d}}+\dfrac{1}{2{{k}_{3}}\dfrac{{{\varepsilon }_{\circ }}A}{d}}=\left( \dfrac{1}{\dfrac{{{\varepsilon }_{\circ }}A}{d}} \right)\left( \dfrac{1}{\left( {{k}_{1}}+{{k}_{2}} \right)}+\dfrac{1}{2{{k}_{3}}} \right)$
Therefore, $\dfrac{1}{{{C}_{123}}}=\left( \dfrac{1}{\dfrac{{{\varepsilon }_{\circ }}A}{d}} \right)\left( \dfrac{1}{\left( {{k}_{1}}+{{k}_{2}} \right)}+\dfrac{1}{2{{k}_{3}}} \right)$. ……..(5)
If all the three dielectrics are replaced by a single dielectric (k) then,
 $\dfrac{1}{{{C}_{123}}}=\dfrac{1}{k}.\left( \dfrac{d}{{{\varepsilon }_{\circ }}A} \right)$ ……..(6).
On comparing equations (5) and (6) we get $\dfrac{1}{\text{k}}\text{ = }\dfrac{1}{{{\text{k}}_{\text{1}}}\text{+}{{\text{k}}_{\text{2}}}}\text{+}\dfrac{1}{\text{2}{{\text{k}}_{\text{3}}}}$

Hence, the correct option is (D).

Note: Different materials have different values of dielectric constant. The perfectly conducting materials have the value dielectric constants as infinity ($k=\infty $). A perfectly insulating material has the value of dielectric constant as zero ($k=0$).
In these types of questions, always remember to convert the dielectrics into capacitors. Then check which are in series and which are in parallel connection and solve accordingly.