Question

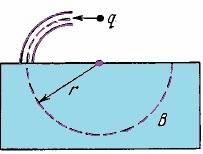
A non-relativistic charged particle flies through the electric field of a cylindrical capacitor and gets into a uniform transverse magnetic field with induction B. In the capacitor the particle moves along the arc of a circle, in the magnetic field, along a semicircle of radius r. The potential difference applied to the capacitor is equal to V, the radii of the electrodes are equal to a and b, with $a < b$. Find the velocity of the particle and its specific charge q/m.

Answer 1

Hint: This is a problem of cylindrical capacitor. Break the question into segments and then solve. Write the formula for electric potential and field for a cylindrical capacitor. Then apply the concept of centripetal and magnetic force on a charge along with the magnetic field and form a relation between the three.

Complete step by step solution:
Step 1: Write the formula electric field and potential for a cylindrical capacitor.
The potential is given as:
$\Delta V = - E. dr$;
Take integration on both the sides:
$\int {\Delta V} = - \int\limits_a^b {E.dr} $;
$\int {\Delta V} = - \int\limits_a^b {\dfrac{\lambda }{{2\pi {\varepsilon _o}r}}.dr} $; ….(Here: $E = \dfrac{\lambda }{{2\pi {\varepsilon _o}r}}$)

Take the constants out of the integration:
$\int {\Delta V} = - \dfrac{\lambda }{{2\pi {\varepsilon _o}}}\int\limits_a^b {\dfrac{1}{r}.dr} $;
Solve the integration by applying the integration property:$\int {\dfrac{1}{r}dr} = \ln r$
\[V = - \dfrac{\lambda }{{2\pi {\varepsilon _o}}}\left[ {\ln r} \right]_a^b\];
Apply the logarithmic property: \[\left[ {\ln r} \right]_a^b = \left[ {\ln b - \ln a} \right]\], in the above equation
\[V = - \dfrac{\lambda }{{2\pi {\varepsilon _o}}}\left[ {\ln b - \ln a} \right]\];
Here, \[\left[ {\ln b - \ln a} \right] = \ln \dfrac{b}{a}\]:
\[V = - \dfrac{\lambda }{{2\pi {\varepsilon _o}}}\ln \dfrac{b}{a}\];

The Electric field is given as:
$E = \dfrac{\lambda }{{2\pi {\varepsilon _o}r}}$;
$E. r = \dfrac{\lambda }{{2\pi {\varepsilon _o}}}$;
Put E in place of $\dfrac{\lambda }{{2\pi {\varepsilon _o}}}$ in the equation for electric potential:
\[V = - E.r\ln \dfrac{b}{a}\];
Write the above equation in terms of electric potential;
\[E = \dfrac{{ - V}}{{r\ln \dfrac{b}{a}}}\];

Step 2: Now, we know the magnetic force on a charge particle:
$F = q. (v \times B)$;
We also know the centripetal force on a charge in a magnetic field
\[{F_c} = \dfrac{{m{v^2}}}{r}\];
 Here the magnetic force supplies the centripetal force, so we can equate them together:
\[q. (v \times B) = \dfrac{{m{v^2}}}{r}\];
Now, electric field is equal to:
\[E = (v \times B)\];
Put the above relation in the equation between centripetal and magnetic force:
\[q. E = \dfrac{{m{v^2}}}{r}\];
Put the value of the electric field \[E = \dfrac{V}{{r\ln \dfrac{b}{a}}}\]. In the above relation
\[q. \dfrac{V}{{r\ln \dfrac{b}{a}}} = \dfrac{{m{v^2}}}{r}\];
Cancel out the common;
\[m{v^2} = q. \dfrac{V}{{\ln (b/a)}}\];
We have already established that the centripetal force ${F_c} = \dfrac{{m{v^2}}}{r}$ is equal to the magnetic force ${F_m} = qvb$:
\[\dfrac{{m{v^2}}}{r} = qvB\];
Cancel out the common variable;
\[\dfrac{{mv}}{r} = qB\];
Take “r” to RHS we have:
\[mv = qBr\];
Put this relation in the equation \[m{v^2} = q. \dfrac{V}{{\ln (b/a)}}\]:
\[(qBr). v = q. \dfrac{V}{{\ln (b/a)}}\];
Cancel out the common variable on both the sides:
\[(Br). v = \dfrac{V}{{\ln (b/a)}}\];
Solve for the velocity,
\[v = \dfrac{V}{{Br\ln (b/a)}}\];
\[v = \dfrac{V}{{Br\ln (b/a)}}\];

Step 3: Find specific charge (q/m).
We know that:
$mv = qBr$;
Write the above equation in terms of q/m.
$\dfrac{q}{m} = \dfrac{{Br}}{v}$;
Put the value of \[v = \dfrac{V}{{Br\ln (b/a)}}\] in the above relation and solve,
$\dfrac{q}{m} = \dfrac{{Br}}{{\dfrac{V}{{Br\ln (b/a)}}}}$;
Solve,
$\dfrac{q}{m} = \dfrac{V}{{Br \times Br\ln (b/a)}}$;
$\dfrac{q}{m} = \dfrac{V}{{B{r^2}\ln (b/a)}}$;

The velocity of the particle and its specific charge q/m is \[v = \dfrac{V}{{Br\ln (b/a)}}\]and $\dfrac{q}{m} = \dfrac{V}{{B{r^2}\ln (b/a)}}$.

Note: It is a very lengthy process, be careful while formulating relations and writing the formulas. Go step by step. First write the potential and electric field and establish a relation between them. Then apply centrifugal force and magnetic force and equate them together. Then apply a magnetic field and find out the velocity and then the specific charge.