
A motor cyclist is riding North in still air at 36 km/h. The wind starts blowing Westward with a velocity 18 km/h. The direction of apparent velocity is:
A. ${{\tan }^{-1}}(\dfrac{1}{2})$ West of North
B. ${{\tan }^{-1}}(\dfrac{1}{2})$ North of West
C. ${{\tan }^{-1}}(\dfrac{1}{2})$ East of North
D. ${{\tan }^{-1}}(\dfrac{1}{2})$ North of East
Answer
221.4k+ views
Hint: The discussion of relative motion in one or more dimensions is where the idea of reference frames was originally introduced. When we state that an object has a given velocity, we mean that this velocity is relative to the so-called reference frame. In daily life, the ground or the earth is assumed to be the reference frame when measuring an object's velocity.
Complete step by step solution:
Two-dimensional relative motion will be able to solve this problem. If you need to determine how fast A is moving relative to B, assume that B is at rest and provide A B's speed in the opposite direction.
Let's take into consideration two objects A and B that are travelling at speeds $V_a$ and $V_b$, respectively, according to some common frame of reference, such as the ground or the earth. Assuming B is at rest, we must determine the velocity of A with respect to B before applying the velocity of B to A in the opposite direction.
${{V}_{ab}}={{v}_{a}}-{{v}_{b}}$
Similar to this, to get the velocity of object B relative to object A, suppose that A is at rest and apply the opposite direction of A's velocity to B's velocity.
${{V}_{ba}}={{v}_{b}}-{{v}_{a}}$
Given: Velocity of cyclist in North $({{V}_{c}})$= 36Km/h and Velocity of wind in west $({{V}_{w}})$= 18Km/h
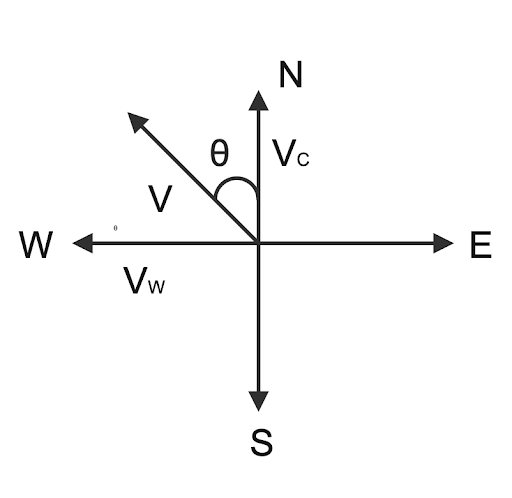
Direction of motion = tanθ
∴ tanθ = $\dfrac{{{V}_{w}}}{{{V}_{C}}}$=$\dfrac{18}{36}$
tanθ = $\dfrac{18}{36}$
∴ θ= ${{\tan }^{-1}}(\dfrac{1}{2})$
From fig. direction of apparent velocity is,
θ= ${{\tan }^{-1}}(\dfrac{1}{2})$ in West of North
Hence, option A is correct.
Note: There is a chance that students may get confused between the concepts of velocity and relative velocity. Velocity is measured with respect to a reference point which is relative to a different point whereas relative velocity is measured with reference to a frame where an object is either moving or at rest with respect to the absolute frame. When viewed from a fixed point of observation, the item is said to be moving absolutely (there is no change in the position of an observer). Relative motion refers to the movement of an object when there is no fixed point of view (the position of the observer changes with respect to time).
Complete step by step solution:
Two-dimensional relative motion will be able to solve this problem. If you need to determine how fast A is moving relative to B, assume that B is at rest and provide A B's speed in the opposite direction.
Let's take into consideration two objects A and B that are travelling at speeds $V_a$ and $V_b$, respectively, according to some common frame of reference, such as the ground or the earth. Assuming B is at rest, we must determine the velocity of A with respect to B before applying the velocity of B to A in the opposite direction.
${{V}_{ab}}={{v}_{a}}-{{v}_{b}}$
Similar to this, to get the velocity of object B relative to object A, suppose that A is at rest and apply the opposite direction of A's velocity to B's velocity.
${{V}_{ba}}={{v}_{b}}-{{v}_{a}}$
Given: Velocity of cyclist in North $({{V}_{c}})$= 36Km/h and Velocity of wind in west $({{V}_{w}})$= 18Km/h

Direction of motion = tanθ
∴ tanθ = $\dfrac{{{V}_{w}}}{{{V}_{C}}}$=$\dfrac{18}{36}$
tanθ = $\dfrac{18}{36}$
∴ θ= ${{\tan }^{-1}}(\dfrac{1}{2})$
From fig. direction of apparent velocity is,
θ= ${{\tan }^{-1}}(\dfrac{1}{2})$ in West of North
Hence, option A is correct.
Note: There is a chance that students may get confused between the concepts of velocity and relative velocity. Velocity is measured with respect to a reference point which is relative to a different point whereas relative velocity is measured with reference to a frame where an object is either moving or at rest with respect to the absolute frame. When viewed from a fixed point of observation, the item is said to be moving absolutely (there is no change in the position of an observer). Relative motion refers to the movement of an object when there is no fixed point of view (the position of the observer changes with respect to time).
Recently Updated Pages
Uniform Acceleration Explained: Formula, Examples & Graphs

JEE Main 2022 (July 26th Shift 1) Physics Question Paper with Answer Key

JEE Main 2022 (June 26th Shift 2) Chemistry Question Paper with Answer Key

Apparent Frequency Explained: Formula, Uses & Examples

JEE Main 2023 (January 30th Shift 2) Chemistry Question Paper with Answer Key

JEE Main 2023 (April 15th Shift 1) Physics Question Paper with Answer Key

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26




