Question

A metre stick weighing 600 g, is displaced through an angle of $60^\circ $ in vertical plane as shown. The change in its potential energy is (g=10ms^-2)


A) 1.5J
B) 15J
C) 30J
D) 45J

Answer 1

Hint: Potential energy of a body(gravitational potential energy) depends on its height from the reference (this case - ground). Height of the metre stick above the ground will be different for the cases- when it is placed vertically and when it is inclined.

Formula Used:
1. Potential energy of object at height h from ground: \[V = mgh\] ……(1)
Where,
g is the acceleration due to gravity
m is the mass of the object
2. Change in potential energy: $\Delta V = {V_f} - {V_i}$ ……(2)
Where,
${V_f}$is the final potential energy
${V_i}$ is the initial potential energy


Complete step by step answer:
Given:
1. Mass of the metre stick m=600 g
2. Inclination of metre stick $\theta = 60^\circ $
3. Height of stick h=1m

To find: The change in its potential energy.

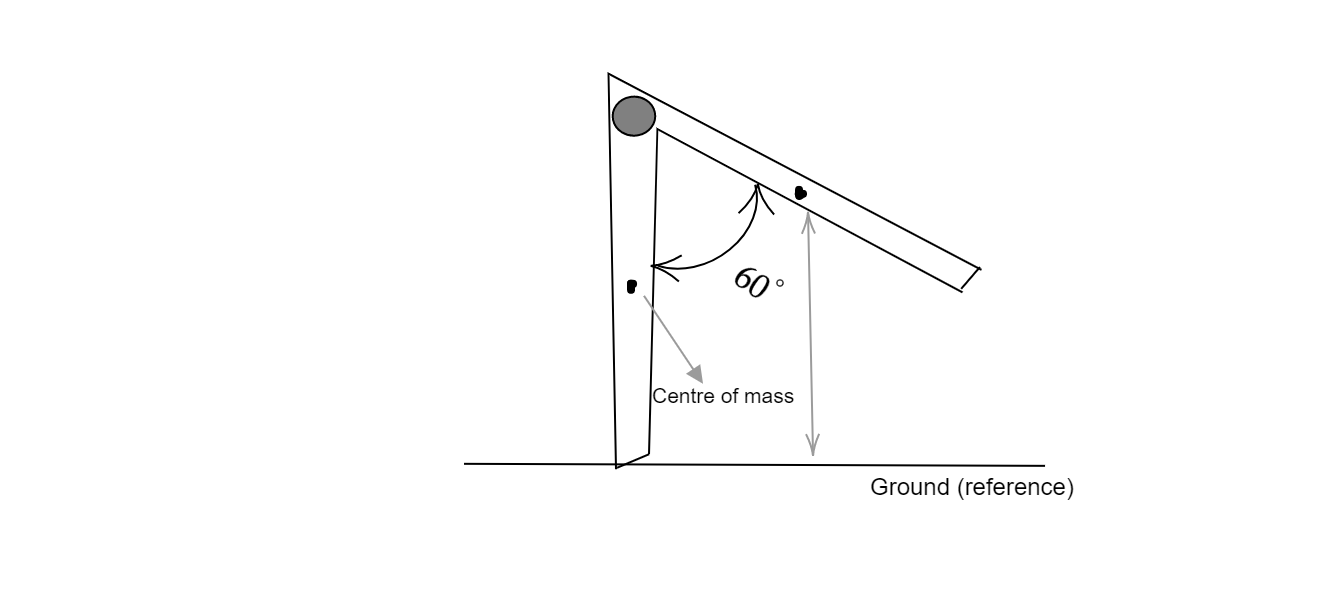
Diagram:



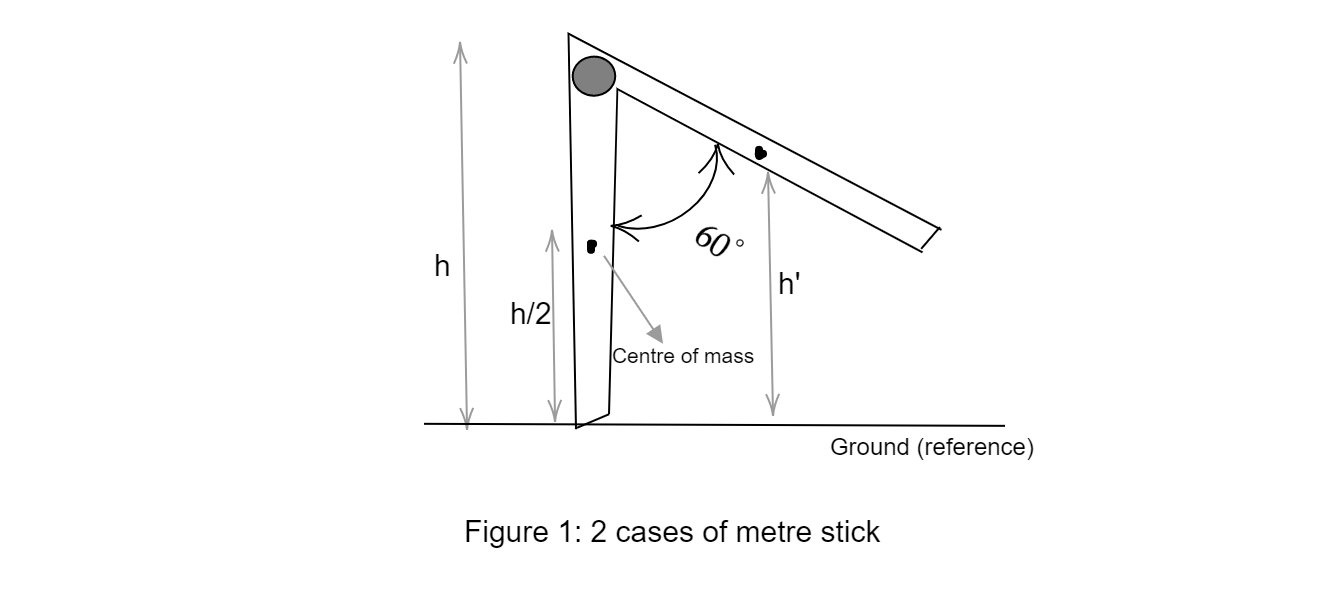
Step 1:
Centre of mass of the stick will lie at its centre point. Let the length of the metre stick be h. When the stick is hanging vertically, the height of the centre of mass from the ground is h/2. Find initial potential of the centre of mass of the metre stick using eq (1):
\[V = mg \times \dfrac{h}{2}\]

Step 2:
When the stick is at $\theta = 60^\circ $, the distance of its centre of mass from the pivot will be h’: $ \Rightarrow \dfrac{h}{2}\cos \theta = \dfrac{h}{2} \times \dfrac{1}{2}$
The height of the centre of mass will be h’:
$ \Rightarrow h' = h - (\dfrac{h}{2} \times \dfrac{1}{2}) = 3\dfrac{h}{4}$
Find final potential of the centre of mass of the metre stick using eq (1):
\[ \Rightarrow V = mg \times \dfrac{{3h}}{4}\]

Step 3:
Calculate the change in potential energy using eq (2):
$
   \Rightarrow \Delta V = (mg \times \dfrac{{3h}}{4}) - (mg \times \dfrac{h}{2}) \\
   \Rightarrow \Delta V = mg \times \dfrac{h}{4} \\
   \Rightarrow \Delta V = \dfrac{{600}}{{1000}} \times 10 \times \dfrac{1}{4} \\
   \Rightarrow \Delta V = 1.5J \\
 $

Final Answer
The change in its potential energy is 1.5J, therefore the correct option is A.


Note: A metre stick has length 1m. Remember to apply the concept of centre of mass. Centre of mass is the point at which all the mass of an extended body can be thought to reside. Net rise in the potential energy is resulting due to rise in the center of mass of the rod which is at half the total length of rod.