
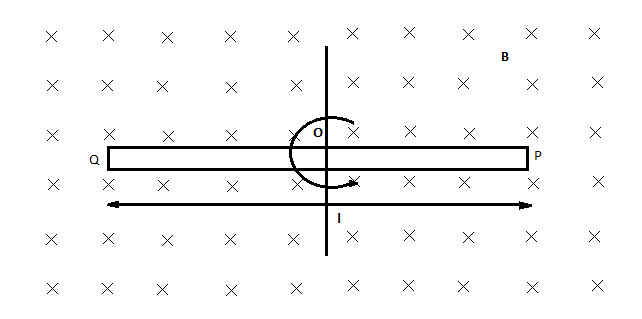
A metallic rod PQ of length $l$ is rotated with an angular velocity $\omega $ about an axis passing through its mid-point O and perpendicular to the plane of the paper, in uniform magnetic field B, as shown in the figure. What is the potential difference developed between the two ends of the rod, P and Q?
Answer
224.7k+ views
Hint: All the points of the rod move when the rod moves with the angular velocity $\omega $. We can find a relation between angular velocity and the translational velocity along the center of mass. Then use the relation equation to find the potential difference between the ends. The rod is rotating along the axis through the midpoint of the rod, perpendicular to the length, therefore divide the rod into two parts, calculate the magnitude of the emf for both the parts and finally calculate the potential difference between two ends.
Complete step by step solution:
Step 1: In the above figure a rod PQ of length $l$ is kept in a magnetic field $\overrightarrow B $. When the rod is rotated along the axis passing through the midpoint of the rod, then some emf will induce in the rod. Now let us split the rod and think about the OP part of the rod of length $\dfrac{l}{2}$ . The center of mass of the OP part of the rod is in the middle of O and P. Therefore, the distance of the center of mass is $\dfrac{l}{4}$. Now express the relation between angular velocity and the translational velocity of the rod.
\[\therefore {v_t} = \omega \times \dfrac{l}{4}\]…..equation(1).
Step 2: we can calculate the potential difference between O and P. express the formula for the potential difference between two ends of the rod
\[\therefore \left| {{V_P}} \right| = B{v_t}L\]
Where $B$ is the magnetic field, $L$is the length of the rod which is $\dfrac{l}{2}$ for OP.
Now substitute the value of ${v_t}$ from equation 1 and $\dfrac{l}{2}$ for $L$ .
$\therefore \left| {{V_P}} \right| = B \times \omega \times \dfrac{l}{4} \times \dfrac{l}{2}$
$ \Rightarrow \left| {{V_P}} \right| = B \times \omega \times \dfrac{{{l^2}}}{8}$
Therefore, the magnitude of the potential difference between O and P is obtained above.
Step 3: Now if you see the figure carefully you will find that all the conditions for the other part of the rod OQ and OP are the same. Therefore the magnitude of the potential difference between O and Q will be the same as between O and P.
$\therefore \left| {{V_Q}} \right| = B \times \omega \times \dfrac{{{l^2}}}{8}$
Step 4: Now calculate the potential difference between P and Q.
$\therefore {V_{PQ}} = {V_Q} - {V_P}$
$ \Rightarrow {V_{PQ}} = B \times \omega \times \dfrac{{{l^2}}}{8} - B \times \omega \times \dfrac{{{l^2}}}{8}$
$ \Rightarrow {V_{PQ}} = 0$
Hence the potential difference between P and Q will be zero.
Note: The potential difference induced by the rotation in a magnetic field may vary if the axis of rotation is not in the mid of the ends, the metallic rod is not uniformly thick, the magnetic field is not uniform, etc. in the relation between angular velocity and translation velocity the distance will vary for each point on the rod but eventually when we will calculate the potential difference between P and Q the result will be the same.
Complete step by step solution:
Step 1: In the above figure a rod PQ of length $l$ is kept in a magnetic field $\overrightarrow B $. When the rod is rotated along the axis passing through the midpoint of the rod, then some emf will induce in the rod. Now let us split the rod and think about the OP part of the rod of length $\dfrac{l}{2}$ . The center of mass of the OP part of the rod is in the middle of O and P. Therefore, the distance of the center of mass is $\dfrac{l}{4}$. Now express the relation between angular velocity and the translational velocity of the rod.
\[\therefore {v_t} = \omega \times \dfrac{l}{4}\]…..equation(1).
Step 2: we can calculate the potential difference between O and P. express the formula for the potential difference between two ends of the rod
\[\therefore \left| {{V_P}} \right| = B{v_t}L\]
Where $B$ is the magnetic field, $L$is the length of the rod which is $\dfrac{l}{2}$ for OP.
Now substitute the value of ${v_t}$ from equation 1 and $\dfrac{l}{2}$ for $L$ .
$\therefore \left| {{V_P}} \right| = B \times \omega \times \dfrac{l}{4} \times \dfrac{l}{2}$
$ \Rightarrow \left| {{V_P}} \right| = B \times \omega \times \dfrac{{{l^2}}}{8}$
Therefore, the magnitude of the potential difference between O and P is obtained above.
Step 3: Now if you see the figure carefully you will find that all the conditions for the other part of the rod OQ and OP are the same. Therefore the magnitude of the potential difference between O and Q will be the same as between O and P.
$\therefore \left| {{V_Q}} \right| = B \times \omega \times \dfrac{{{l^2}}}{8}$
Step 4: Now calculate the potential difference between P and Q.
$\therefore {V_{PQ}} = {V_Q} - {V_P}$
$ \Rightarrow {V_{PQ}} = B \times \omega \times \dfrac{{{l^2}}}{8} - B \times \omega \times \dfrac{{{l^2}}}{8}$
$ \Rightarrow {V_{PQ}} = 0$
Hence the potential difference between P and Q will be zero.
Note: The potential difference induced by the rotation in a magnetic field may vary if the axis of rotation is not in the mid of the ends, the metallic rod is not uniformly thick, the magnetic field is not uniform, etc. in the relation between angular velocity and translation velocity the distance will vary for each point on the rod but eventually when we will calculate the potential difference between P and Q the result will be the same.
Recently Updated Pages
JEE Main 2025-26 Experimental Skills Mock Test – Free Practice

JEE Main 2025-26: Magnetic Effects of Current & Magnetism Mock Test

JEE Main 2025-26 Atoms and Nuclei Mock Test – Free Practice Online

JEE Main Mock Test 2025-26: Optics Chapter Practice Online

The work done in slowly moving an electron of charge class 12 physics JEE_Main

The value of the resistor RS needed in the DC voltage class 12 physics JEE_Main

Trending doubts
JEE Main 2026: City Intimation Slip and Exam Dates Released, Application Form Closed, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Hybridisation in Chemistry – Concept, Types & Applications

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Understanding Atomic Structure for Beginners

Understanding Electromagnetic Waves and Their Importance




