Question

A mass of $1Kg$ is suspended by a thread.it is first lifted up with an acceleration of $4.9m{s^{ - 2}}$, and then lowered with an acceleration of $4.9m{s^{ - 2}}$. What is the ratio of tension in the two cases?
A) $3:1$
B) $1:2$
C) $1:3$
D) $2:1$

Answer 1

Hint: An external acceleration and retardation is given to the system. While lifting the ball the external acceleration is opposite to the acceleration due to gravity, so, it is the retardation. When the ball is lowered the acceleration is in the direction of the acceleration due to gravity, so, it is the acceleration. Likewise there is an external force acting along with the force of gravity but in the rising case it is in the opposite direction and in the lowering case it is in the same direction.

Formulae used:
$F = ma$
Where $F$ is the force acting on the body, $m$ is the mass of the body and $a$ is the acceleration acting on the body.
$W = mg$
Where $W$ is the force acting on the body, $m$ is the mass of the body and $g$ is the acceleration due to gravity acting on the body.

Complete step by step answer:
In the question, two cases are given. Let us see the free body diagram in each case.
Case 1

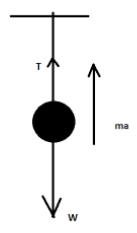
In the above diagram, a mass of $1Kg$ is suspended from a thread. Its weight is acting vertically downwards and the tension is acting in vertically upwards direction. So the net force will be,
$ \Rightarrow T - W = ma$
$ \Rightarrow T - mg = ma$
$ \therefore T = ma + mg = m(a + g)$
Substituting the values of $m = 1Kg$, $a = 4.9m{s^{ - 2}}$ and $g = 9.8m{s^{ - 2}}$
$ \therefore T = 1(4.9 + 9.8) = 14.7N$

Case 2

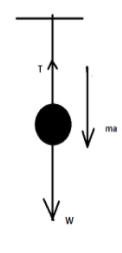
In the above diagram, a mass of $1Kg$ is suspended from a thread. Its weight is acting vertically downwards and the tension is acting in vertically upwards direction. So the net force will be,
$ \Rightarrow W - T = ma$
$ \Rightarrow mg - T = ma$
$ \therefore T = mg - ma = m(g - a)$
Substituting the values of $m = 1Kg$, $a = 4.9m{s^{ - 2}}$ and $g = 9.8m{s^{ - 2}}$
$ \Rightarrow T = 1(9.8 - 4.9) = 4.9N$
Hence the ratio of the tension is,
$ \therefore \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{14.7}}{{4.9}} = \dfrac{3}{1}$

So the answer will be option (A) i.e. $3:1$.

Note: If the ball was just tied to the string and the entire system was in rest then the tension in the string will be directly equal to the weight of the ball. But since there was an external acceleration and an external retardation, the ball had some net acceleration in both the cases. Hence, the value of tension was different for both the cases.