Question

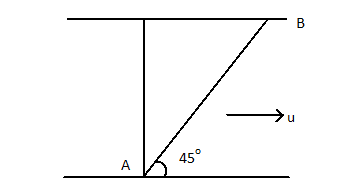
A man wants to reach point B on the opposite bank of a river flowing at a speed $u$ as shown in figure, At What minimum speed relative to water should the man have so that he can reach point B? In which direction should I swim?

Answer 1

Hint: The proceeding approach will be the relative motion concept. We going to assume boatman’s velocity with respect to water So that it will become easy to examine boatman’s motion in water
Before proceeding student must know what does relative approach mean, In most simple words, Relative motion is the understanding of the motion of an object with respect to some other moving or stationary object, for example a person is sitting in the moving bus is at zero velocity relative to the bus, is moving at the same velocity as the bus with respect to the ground.

Complete step by step solution:
According to the question given we have to find the minimum speed so that the boatman will reach at point B starting from A.
Let v be the velocity of a boatman with respect to water or velocity in still water, u is the velocity of water.
Resultant of v and u should be along AB.
Let the absolute velocity of boatman (velocity with respect to ground) be $v_b^ \to $ which is along AB
So, the resultant of u and $v_b^ \to $ should be along AB
Let us resolve component of v along x and y direction
Where ${v_x}$ and ${v_y}$ be the components along Horizontal and vertical directions respectively
So, coming to the calculation part
$\Rightarrow {v_x}$$ = u - v\sin \theta $
$\Rightarrow {v_y} = v\cos \theta $
Further $\tan \theta = \dfrac{{perpendicular}}{{base}} = \dfrac{{{v_y}}}{{{v_x}}}$
So, $\tan 45$
$
\Rightarrow \dfrac{{v\cos \theta }}{{u - v\sin \theta }} = 1\,\,\,\,\,\,\,\,(\tan 45 = 1) \\
\Rightarrow v\cos \theta = u - v\sin \theta \\
  \therefore v = \dfrac{u}{{\sin \theta + \cos \theta }} \\
 \Rightarrow v = \dfrac{u}{{\sqrt 2 \sin (\theta + 45)}} \\
 $
So, v is minimum when the denominator is maximum, In denominator we have sin whose maximum value is 1.
$
   \Rightarrow \theta + 45 = 90 \\
   \Rightarrow \theta = {45^o} \\
 $
And, $v = \dfrac{u}{{\sqrt 2 }}$
Speed relative to water is $\dfrac{u}{{\sqrt 2 }}$.
Direction is 45 degrees to the north west.

Note: The question above is for minimum speeds but for minimum distance we should move in such a direction that our motion will become along AC relative to water and for minimum time motion will be along AC direct.