Question

A man running along a straight road with uniform velocity $\vec u = u\hat i$ feels that the rain is falling vertically down along $-j$. If he doubles his speed, he finds that the rain is coming at an angle $\theta $ with the vertical. The velocity of the rain with respect to the ground is:
$\left( A \right)ui - u\tan \theta \hat j$
$\left( B \right)ui - \dfrac{u}{{\tan \theta }}\hat j$
$\left( C \right)u\tan \theta - u\hat j$
$\left( D \right)\dfrac{u}{{\tan \theta }}i - u\hat j$

Answer 1

Hint: If two bodies are moving along the same line in the same direction with velocities ${V_A}$ and ${V_B}$ relative to earth then the magnitude of the velocity of \[A\] relative to \[B\] is given by ${V_A} - {V_B} = {V_{AB}}$. The velocity of one object with respect to some frame is known as the reference frame. Draw a free-body using the data given above and determine the velocity of the rain with respect to the ground.

Complete step by step solution:
The velocity of one object with respect to some frame is known as the reference frame. Objects move in a straight line in one-dimension motion. So, there are only two possible cases are objects are moving in the same direction and Objects are moving in the opposite direction
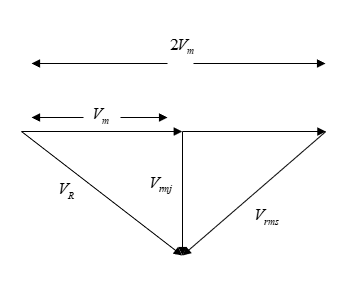
The velocity of man =$\vec u = u\hat i$
Let the velocity of the rain =$\vec v = x\hat i + y\hat j$

Let us find the velocity of rain with respect to man = ${V_R} = \left( {x - u} \right)\hat i + y\hat j$
Rain is falling vertically down then the \[\;x\] component is zero and then the \[y\] component is along the negative direction.
Hence, the velocity of rain=$u\hat i + y\hat j$
When he doubles the speed velocity of rain with respect to man =${V_R}$
${V_R} = u\hat i + y\hat j - 2u\hat i$
${V_R} = - u\hat i + y\hat j$
Now the rain is falling at the angle $\theta $ to the vertical
$\tan \theta = \dfrac{{ - u}}{y}$
The velocity of rain with respect to ground
$V = x\hat i + y\hat j$
$V = u\hat i - \dfrac{y}{{\tan \theta }}\hat j$
Hence option $\left( B \right)$ is the right option.

Note: Objects move in a straight line in one-dimension motion. So, there are only two possible cases: objects are moving in the same direction and Objects are moving in the opposite direction. If two bodies are moving along the same line in the same direction with velocities ${V_A}$ and ${V_B}$ relative to earth then the magnitude of the velocity of \[A\] relative to B is given by ${V_A} - {V_B} = {V_{AB}}$.