Question

A jar of height h is filled with a transparent liquid of refractive index,\[\mu \] . At the centre of the jar, on the bottom surface is a dot. Find the minimum diameter of a disc such that when it is placed on the top surface symmetrically about the centre, the dot is invisible.

Answer 1

Hint: The dot is invisible, due to the phenomenon of total internal reflection. Total internal reflection takes place when the angle of incidence exceeds the critical angle.

Complete step by step answer:
  
Let us understand the concept of total internal Reflection from the following definitions:
The phenomenon of reflection of total light when the light travelling in a denser medium strikes the interface separating the denser and the rarer medium at an angle greater than the critical angle, this is referred to as total internal reflection.
Now, we come across a term, critical angle. This critical angle is the angle of incidence in the denser medium, for which the angle of refraction in the rarer medium becomes\[{90^o}\] .
Now coming to the question, it is given that:
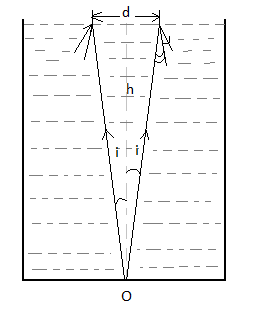
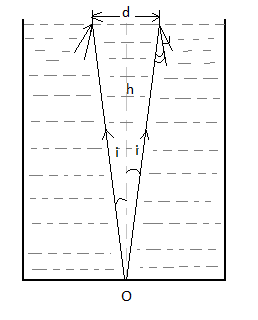
Height of the jar=h
Refractive index of the transparent medium is =\[\mu \]
We need to find the diameter of the ring, which when placed symmetrically on the top surface, the dot O at the bottom surface becomes invisible.
In order to make the dot invisible, rays marked OA and OB must suffer total internal Reflection.
Let \[\angle AOC\] be the angle of incidence marked as I in the diagram.
In\[\Delta AOC\] :
\[\tan i = \dfrac{{AC}}{{OC}} = \dfrac{{d/2}}{h}\]
 Now, we know, for total internal reflection to occur, \[\angle i \geqslant \angle c\]
So, \[\sin i = \sin c\]
Applying Snell’s law:
We know,
 \[\dfrac{{\sin i}}{{\sin r}} = \mu \]
Where, r= angle of refraction, which is \[{90^o}\] .
We know, if refractive index of media a with respect to b (air to water) is denoted by\[\mu \], then refractive index of b with respect to a ( water to air) is denoted by \[\dfrac{1}{\mu }\]
Therefore, the previous equation can also be written as:
\[\sin i = \dfrac{1}{\mu }\]
Drawing the triangle from the above equation:

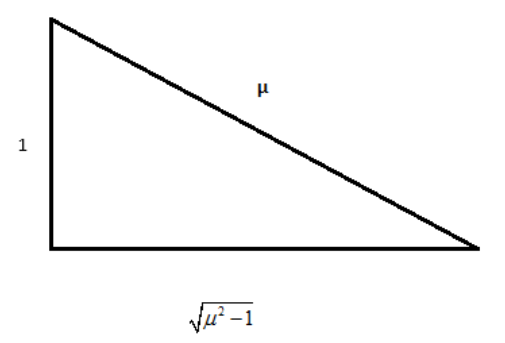
\[\tan i = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}\]
Equating values of\[\tan i\] :
\[\dfrac{d}{{2h}} = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}\]
Solving the equation, we get:
\[d = \dfrac{{2h}}{{\sqrt {{\mu ^2} - 1} }}\]
This is the required value of diameter.

Note: Total internal reflection takes place when light ray travels from optically denser medium to the rarer medium. Here, (water-air surface). The rarer medium is the medium, in which the speed of light is more whereas the denser medium is the one where the speed of light is less.