Question

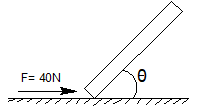
A homogeneous rod of mass $3Kg$ is pushed along a smooth horizontal surface by a horizontal force $F = 40N$ . The angle ‘ $\theta $ ’ is the angle (in degree) for which the rod has pure translational motion. What is the value of $\theta $ minus $30$ degree is? $(g = 10m/{s^2})$

Answer 1

Hint:Here in this question, we have to find the value of $\theta $ minus $30$ degree for a rod in pure translational motion. For which we should know that, in situations where acceleration is unknown, this equation is helpful. Assume you are aware of an object's initial and final speeds as well as its duration of motion. The distance travelled is simply the average of those two velocities multiplied by the time, according to this equation.

Formula Used:
Since, for this question the normal reaction value will be, $N = mg$.
Torque about the centre of mass,
$F\sin \theta \times \dfrac{L}{2} - N\cos \theta \times \dfrac{L}{2} = 0$

Complete step by step solution:
As we all know, the pure translation motion stands for where there is no rotation or there is no external torque over the centre of mass. From free body diagram, we have

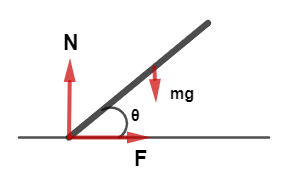
By taking Anti clockwise as the position, the torque about the centre of mass,
$F\sin \theta \times \dfrac{L}{2} - N\cos \theta \times \dfrac{L}{2} = 0$
By taking all the signs as positive we get,
$F\sin \theta \times \dfrac{L}{2} = N\cos \theta \times \dfrac{L}{2}$
By cancelling out the common values we get the equation as,
$F\sin \theta = N\cos \theta $

By taking theta quantities one side and left on another side,
$\dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{N}{F}$
By using the trigonometric identity, $\dfrac{{\sin \theta }}{{\cos \theta }} = \tan \theta $ in the above equation we get,
$\tan \theta = \dfrac{N}{F}$
We know the value of N by putting the value, we get the resultant as,
$\tan \theta = \dfrac{{mg}}{F}$

As according to question, we have the respective values as, $m = 3Kg$ , $(g = 10\,m/{s^2})$ and $F = 40N$, putting the whole values in the above equation, we get,
$\tan \theta = \dfrac{{3 \times 10}}{{40}}$
By completing the further calculation, we get that,
$\theta = {37^ \circ }$
As according to the question, the value of $\theta $ minus $30$ degree for a rod is,
$\therefore {37^ \circ } - {30^ \circ } = {7^ \circ }$

Therefore, the correct answer for the value of $\theta $ minus $30$ degree for a rod is ${7^ \circ }$.

Note: Pure translational motion is when an object travels in a way that all of its constituent particles move in parallel to one another. Every place on the body experiences the same magnitude and direction of velocities and accelerations during this sort of motion.