Question

A hollow cylinder of length $l$ and radii $a$ and $b$ is filled with a material of resistivity $\rho $ and is connected to a battery of emf $E$ through an ammeter. Find the current through the ammeter.
A) $\dfrac{{E\pi l\left( {{b^2} - {a^2}} \right)}}{{\rho \lambda }}$
B) $\dfrac{{E\pi l}}{{\left( {\rho {{\log }_e}\dfrac{b}{a}} \right)}}$
C) $\dfrac{{E2\pi l}}{{\left( {\rho {{\log }_e}\dfrac{b}{a}} \right)}}$
D) $\dfrac{{E2\pi l}}{{\left( {\rho {{\log }_e}\dfrac{a}{b}} \right)}}$

Answer 1

Hint: Here the resistance offered to the flow of current through the ammeter is the resistance of the entire cylinder. The current is obtained using Ohm’s law. The resistance of the entire cylinder can be obtained by integrating the resistance of a small element of the given cylinder between the radii of the hollow cylinder.

Formulas used:
i) Ohm’s law gives the current through a circuit as $I = \dfrac{V}{R}$ where $V$ is the potential difference across the circuit and $R$ is the resistance offered to the flow of current in the circuit.
ii) The resistance of a body is given by, $R = \dfrac{{\rho l}}{A}$ where $\rho $ is the resistivity of the material of the body, $l$ is the length of the body and $A$ is the area of the body.

Complete step by step answer:
Step 1: Sketch a figure describing the given circuit and obtain the resistance of an elemental area of the cylinder.

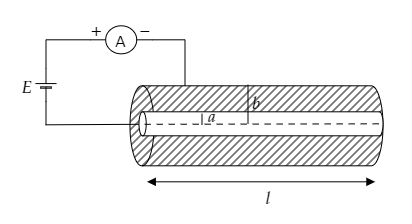
The above figure represents the circuit diagram of the problem at hand.
The length of the cylinder is given to be $l$ and $\rho $ is the resistivity of the material of the cylinder.
The radii of the cylinder are given to be $a$ and $b$.
The potential difference across the circuit is given to be $V = E$ .
Let $R$ be the resistance of the cylinder and $I$ be the current through the ammeter.
We now consider a small element of the cylinder of radius $r = x$ and length $l = dx$ as shown in the figure below. The area of the small element will be $A = 2\pi xl$.

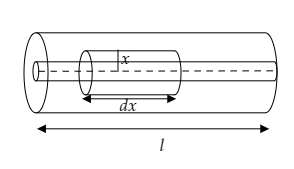
Now the resistance of the small element can be expressed as $dR = \dfrac{{\rho dx}}{{2\pi xl}}$ ------ (1).

Step 2: Integrate equation (1) to obtain the resistance of the entire cylinder.
The resistance offered by the circuit to the flow of current is obtained by integrating equation (1) between the limits $a$ and $b$ .
i.e., $R = \int\limits_a^b {dR} $ -------- (2)
Substituting equation (1) in (2) we get, $R = \int\limits_a^b {\dfrac{{\rho dx}}{{2\pi xl}} = \dfrac{\rho }{{2\pi l}}\int\limits_a^b {\dfrac{{dx}}{x}} } $
On integrating and applying the limits we get, $R = \dfrac{\rho }{{2\pi l}}\left[ {{{\log }_e}b - {{\log }_e}a} \right]$ -------- (A)
$ \Rightarrow R = \dfrac{\rho }{{2\pi l}}{\log _e}\left( {\dfrac{b}{a}} \right)$
Thus the resistance of the entire cylinder is $R = \dfrac{\rho }{{2\pi l}}{\log _e}\left( {\dfrac{b}{a}} \right)$ .

Step 3: Using Ohm’s law obtain the current through the ammeter.
Ohm’s law gives the current through the ammeter as $I = \dfrac{E}{R}$ -------- (3)
Substituting for $R = \dfrac{\rho }{{2\pi l}}{\log _e}\left( {\dfrac{b}{a}} \right)$ in equation (3) we get, $I = \dfrac{E}{{\left( {\dfrac{\rho }{{2\pi l}}{{\log }_e}\left( {\dfrac{b}{a}} \right)} \right)}}$
$ \Rightarrow I = \dfrac{{E2\pi l}}{{\rho {{\log }_e}\left( {\dfrac{b}{a}} \right)}}$
Thus the current through the ammeter is $I = \dfrac{{E2\pi l}}{{\rho {{\log }_e}\left( {\dfrac{b}{a}} \right)}}$

So the correct option is C.

Note: The integral of $\dfrac{1}{x}$ is given by, $\int {\dfrac{{dx}}{x} = \ln x = {{\log }_e}x} $. This is obtained in equation (A). Also, we have ${\log _e}\dfrac{a}{b} = {\log _e}a - {\log _e}b$. This result is used to simplify the expression for the resistance of the entire cylinder. The integration of any function will always be easier if we take the constants involved in the function outside the integral.