Question

A galvanometer of resistance $25\Omega $ is connected to a battery of $2V$ along with a resistance in series. When the value of this resistance is $3000\Omega $ a full- scale deflection $30units$ is obtained in the galvanometer. To reduce this deflection to $20units$, the resistance in series will be:
(A) $1991.66\Omega $
(B) $5413\Omega $
(C) $2000\Omega $
(D) $6000\Omega $

Answer 1

Hint From the diagram, we can see that the battery, the galvanometer, and the resistance are in series with each other. The internal resistance of the galvanometer, $r$ is $25\Omega $. The initial resistance in series is $3000\Omega $. Thus we apply Kirchhoff’s Voltage Law in the above circuit to get the current flowing through the circuit. Next, we insert a new resistance $x$ in series with the previous resistance to get the new current flow.

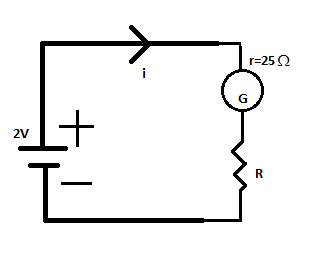
Complete Step by step solution Applying Kirchhoff’s Voltage Law in the above circuit, we get
$2V = iR + ir$ .
The values of $R = 3000\Omega $, and $r = 25\Omega $ are given.
Substituting these values in the given equation, we get
$ \Rightarrow 2V = i(3000\Omega + 25\Omega )$
$ \Rightarrow i = \dfrac{2}{{3025}}A$
This value is described as $30units$ when the deflection of the galvanometer is at full scale.
Thus if $i = \dfrac{2}{{3025}}A = 30 units$ then
$1unit$ is $\dfrac{2}{{3025 \times 30}}A$.
Similarly, deflection $20units$ is equal to $\dfrac{{2 \times 20}}{{3025 \times 30}}A$current flow through the circuit which is the new current $I$ .
Thus keeping the numerator same, the denominator turns out to be
$\dfrac{2}{{3025 \times 1.5}}A = \dfrac{{2V}}{{4537.5\Omega }}$
; i.e. the denominator turns out to be $(4512.5 + 25)\Omega $.
We now get the required net resistance of the new circuit to be $4537.5\Omega $, which is including the internal resistance of the galvanometer.
This is because we can compare this equation with the K.V.L. equation of the new circuit, where $2V = I(r + R) = \dfrac{{2 \times 20}}{{3025 \times 30}}(25\Omega + R)$.
On further simplifying we get,
$ \Rightarrow 2 \times \dfrac{{3025 \times 30}}{{2 \times 20}} = 25 + R$
$ \therefore R + 25\Omega = (4512.5 + 25)\Omega $
Thus we get the required value of the new resistance $R$ as $4512.5\Omega $.

Therefore the correct option is not present in the given question.

Note A galvanometer measures the amount of current flowing through a given circuit. Here the galvanometer resistance is constant since we use the same galvanometer for both the readings. The value of the resistance $R$ changes as we wish to decrease the value of current passing through the galvanometer.