Question

A current I flow through a closed loop as shown in figure. The magnetic field induction at the centre O is:


$\left( A \right)\dfrac{{{\mu _0}I}}{{4\pi R}}\theta $
$\left( B \right)\dfrac{{{\mu _0}I}}{{4\pi R}}\left( {\theta + \sin \theta } \right)$
$\left( C \right)\dfrac{{{\mu _0}I}}{{4\pi R}}\left( {\pi - \theta + \sin \theta } \right)$
$\left( D \right)\dfrac{{{\mu _0}I}}{{4\pi R}}\left( {\pi - \theta + \tan \theta } \right)$

Answer 1

Hint: The relation between current and magnetic field produced by the current is given by the Biot Savart law. Here the current is flowing clockwise. Apply the Biot Savart law on the loop PSR and PQ to obtain the magnetic field of a circle and magnetic field of a segment. Sum of the two magnetic fields gives the resultant magnetic field.

Formula used:
\[B = \dfrac{{{\mu _0}I}}{{2a}}\]
It is the magnetic field of the circle where $B$ is the magnetic field, $I$ is the current.

Complete step to step answer:
The magnetic field produced due to a current carrying segment is given by Biot Savart law. It is a vector quantity. In order to determine the magnetic field produced at a point due to this small element, one can use Biot-Savart’s Law.
Biot-Savart’s law, the magnetic field depends on
Is directly proportional to the current
Is directly proportional to the length
Current is flowing clockwise. Now let us apply the magnetic field due to the loop PSQ. Then magnetic field of a segment is
\[{B_{PSQ}} = \dfrac{{{\mu _0}I}}{{2R}}\left( {\dfrac{{2\pi - 2\theta }}{{2\pi }}} \right) - - - - - \left( 1 \right)\]
Magnetic field due to the loop PQ. The magnetic field of is
\[B = \dfrac{{{\mu _0}I}}{{2a}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right) - - - - - \left( 2 \right)\]
Here a is the perpendicular distance from the point to the wire.


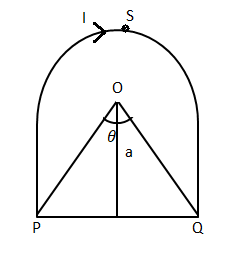
Here $a = r\cos \theta $
${B_{PQ}} = \dfrac{{{\mu _0}I}}{{4\pi R\cos \theta }}\left( {2\sin \theta } \right)$
${B_{PQ}} = \dfrac{{{\mu _0}I}}{{4\pi R}}\left( {2\tan \theta } \right)$
${B_{RES}} = \dfrac{{{\mu _0}I}}{{4\pi R}}\left( {2\pi - 2\theta } \right) + \dfrac{{{\mu _0}I}}{{4\pi R}}\left( {2\tan \theta } \right)$
${B_{RES}} = \dfrac{{{\mu _0}I}}{{4\pi R}}\left( {\pi - \theta + \tan \theta } \right)$

Hence option $\left( D \right)$ is the right option.

Note: Biot-Savart’s Law for the magnetic field has certain similarities as well as differences with the coulomb's law. In Biot-Savart’s Law the magnetic field is directly proportional to the sine of the angle. The magnetic field produced due to a current carrying segment is given by Biot Savart law. Biot-Savart’s Law is a vector quantity .