Question

A car moves north at a speed of $54km{h^{ - 1}}$ for $1hr$. Then it moves eastward with the same speed for the same duration. The average speed and average velocity of car for complete journey is
(A) $54km{h^{ - 1}},0$
(B) $15m{s^{ - 1}},\dfrac{{15}}{{\sqrt 2 }}m{s^{ - 1}}$
(C) $0,0$
(D) $0,\dfrac{{54}}{{\sqrt 2 }}m{s^{ - 1}}$

Answer 1

Hint: Here we are using the concept of average speed and average velocity to solve this problem. For that you need to know what is average speed and average velocity.
Average speed: It can be explained as the total distance travelled by a car or bike or any vehicle for a particular time interval and we divide the total distance travelled by total time taken.
Average velocity: It is calculated as the total displacement of the object in that time interval divided by total time taken.

Complete step by step solution:

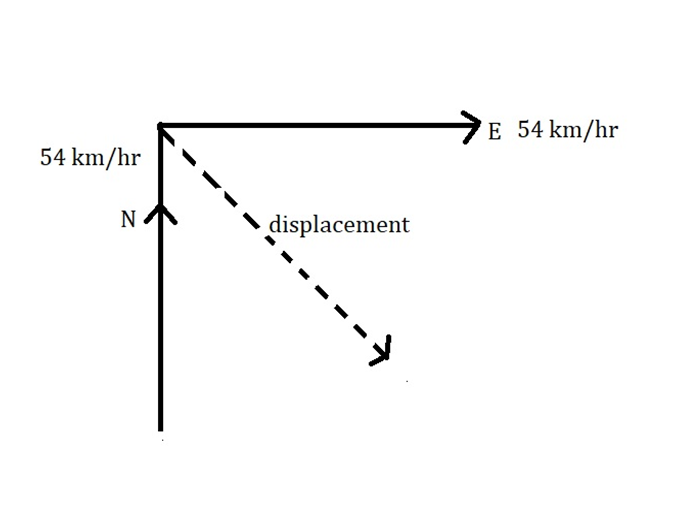
First of all we need to know which formula we are going to use here to solve this problem.
${\text{Average speed}}\left( {{v_{av}}} \right) = \dfrac{{{\text{Total distance travelled}}}}{{{\text{Total time taken}}}}$
$ \Rightarrow {V_{av}} = \dfrac{{54 + 54}}{2}$
$ \Rightarrow v = 54km{h^{ - 1}}$
$ \Rightarrow {v_{av}} = 15m{s^{ - 1}}$
${\text{Average Velocity}}\left( {{{\vec v}_{av}}} \right) = \dfrac{{{\text{Total displacement}}}}{{{\text{Total time taken}}}}$
$ \Rightarrow {v_{av}} = \dfrac{{\sqrt {{{\left( {54} \right)}^2} + {{\left( {54} \right)}^2}} }}{2}$
$ \Rightarrow {\vec v_{av}} = \dfrac{{54\sqrt 2 }}{2}$
$ \Rightarrow {v_{av}} = \dfrac{{54}}{{\sqrt 2 }}km{h^{ - 1}}$
$ \Rightarrow {v_{av}} = \dfrac{{15}}{{\sqrt 2 }}m{s^{ - 1}}$

The correct answer is option B

Additional information:
These are some important differences regarding speed and velocity.
Velocity is a vector quantity whereas speed is a scalar quantity.
Speed of an object can be positive or zero whereas velocity can be negative, zero or positive.
Even if the average velocity can be zero since the velocity depends on displacement but average speed can never be zero.

Note:
Acceleration is the rate of change of velocity. It is a vector quantity.
Average acceleration: It is defined as the total change in velocity divided by total time taken during a particular time interval.
Gravitational acceleration: It is the free fall acceleration. For example when an object is dropped from the top of a building it undergoes gravitational acceleration.
Tangential acceleration: It is measured as the rate of change of tangential velocity with a specific radius in the circular path.