Question

When a car is at rest, its driver sees raindrops falling on it vertically. When driving the car with speed v, he sees that raindrops are coming at an angle \[{60^0}\] from the horizontal. On further increasing the speed of the car to \[\left( {1 + \beta } \right)v\] , this angle changes to \[{45^0}\]. Then find the value of \[\beta \].
A. 0.50
B. 0.73
C. 0.37
D. 0.41

Answer 1

Hint: Before we start addressing the problem, let’s have a look at the data. We know that the angle of rainfall is \[{60^0}\] and changes to \[{45^0}\] upon acceleration. The initial speed of the car is v and the final speed is \[\left( {1 + \beta } \right)v\] and we need to solve for \[\beta \]. Here, the concept of relative velocity is used to solve the problem.

Formula Used:
To find the velocity of rain with respect to the car is given by,
\[\overrightarrow {{v_{RC}}} = \overrightarrow {{v_{RG}}} - \overrightarrow {{v_{CG}}} \]……….. (1)
Where, \[\overrightarrow {{v_{RG}}} \] is velocity of rain wrt ground and \[\overrightarrow {{v_{CG}}} \] is velocity of car wrt ground.

Complete step by step solution:


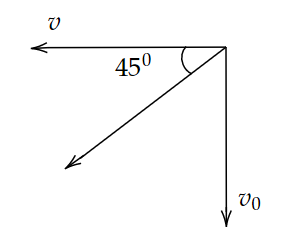
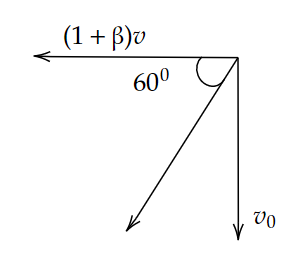
Image: Angle made by raindrop with respect to the ground.

Case (1): When the car is at rest, the driver sees that the raindrop is falling vertically then the velocity of the raindrop is \[{v_0}\]. i.e., in vector form, \[{v_0}\left( { - \widehat j} \right)\].

Case (2): When the driver starts the car, then he sees that the raindrops are falling at an angle of \[{60^0}\] when the car is moving with the speed of v i.e., in vector form, \[{v_0}\widehat i\].

Case (3): On further increasing the speed of the car, its velocity becomes \[\left( {1 + \beta } \right)v\] then the angle will be \[{45^0}\]. Now we need to find the \[\beta \]. i.e., in vector form, \[\left( {1 + \beta } \right)v\widehat i\]

In order to do that first, we need to find the velocity of rain with respect to the ground and the velocity of the car with respect to the ground i.e.,
\[\overrightarrow {{v_{RC}}} = \overrightarrow {{v_{RG}}} - \overrightarrow {{v_{CG}}} \]
On considering case (1) and case (2) we get,
\[\overrightarrow {{v_{RC}}} = {v_0}\left( { - \widehat j} \right) - v\widehat i\]
\[\Rightarrow \overrightarrow {{v_{RC}}} = - \left( {v\widehat i + {v_0}\widehat j} \right)\]

Now, we can find the value of \[{v_0}\]in above equation,
\[\tan {60^0} = \left( {\dfrac{{{v_0}}}{v}} \right)\]
\[\sqrt 3 = \left( {\dfrac{{{v_0}}}{v}} \right)\]
\[ \Rightarrow {v_0} = \sqrt 3 v\]……… (2)
Now, we will find \[\beta \] using equation (1) as,
\[\overrightarrow {{v_{RC}}} = \overrightarrow {{v_{RG}}} - \overrightarrow {{v_{CG}}} \]
\[\Rightarrow \overrightarrow {{v_{RC}}} = - {v_0}\widehat j - \left( {1 + \beta } \right)\widehat i\]

In order to find the value of \[{v_0}\]in above equation,
\[\tan {45^0} = \dfrac{{{v_0}}}{{\left( {1 + \beta } \right)v}}\]
\[\Rightarrow 1 = \dfrac{{{v_0}}}{{\left( {1 + \beta } \right)v}}\]
\[\Rightarrow {v_0} = \left( {1 + \beta } \right)v\]…………. (3)
Equate equations (2) and (3) we get,
\[\sqrt 3 v = \left( {1 + \beta } \right)v\]
\[ \Rightarrow \beta = \sqrt 3 - 1\]
\[ \therefore \beta = 0.732\]
Therefore, the value of \[\beta \] is 0.732

Hence, Option B is the correct answer

Note:Velocity is defined as the distance covered by an object per unit time. Velocity is a vector quantity. The apparent speed of object A to an observer travelling alongside object B is the velocity of item A in relation to object B.