Question

A capillary tube is dipped in water up to length \[\left( l \right)\], the level of water reaches up to height $\left( h \right)$. Now the end which is inside the water is closed and the capillary tube is put outside the water and that closed-end is opened if \[\left( {l > h} \right)\], the height of the remaining water column in the capillary will be:
A) $0$
B) $l + h$
C) $2h$
D) $h$

Answer 1

Hint: The rise of water in the capillary is due to adhesive forces dominating over the cohesive force of the liquid. The rise of water in the capillary also depends upon the density of the water.
If the capillary is taken out of the water and if it contains liquid it is because the surface tension on the lower side of the tube was able to hold the weight of the water above it
Theory:
Surface Tension: Liquid surfaces tend to shrink into the minimum surface area possible. Surface tension allows insects (e.g., mosquitoes), to sit on the surface without drowning
 When the capillary tube is dipped into the water, the water will rise to a height of$h$, now as the capillary is taken out of the water, and the hand is removed from the bottom there a meniscus will be formed due to surface tension.

Complete step by step solution:

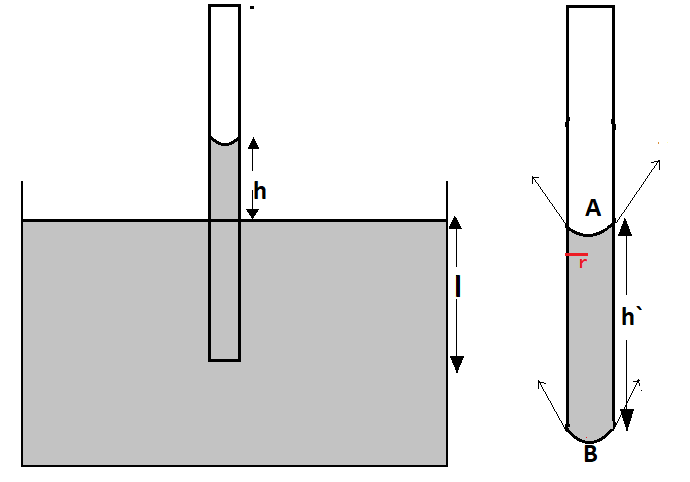
The height $h$ up to which the water will rise in the tube when it is dipped in water is given by
 $h = \dfrac{{2T\operatorname{Cos} \theta }}{{r\rho g}}$
Where
$h$is the height up to which water rises in a tube
$T$ is the surface tension
$\theta $ is the angle made by the meniscus
$r$ is the radius of the capillary tube
$\rho $is the density of water
$g$ gravity
Now when the tube is taken out of the water,
Let the new height be $h`$
The weight will be supported by total upward force due to surface tension
on both side A and B
The upward force is given by
$F = 2\pi rT\cos \theta $
Here the upward force is acting at 2 points A and B i.e., top meniscus and bottom meniscus
So total upward force will be
$\Rightarrow {F_{total}} = 2 \times 2\pi rT\cos \theta $
Now this total force will be supporting the weight of the water inside the tube
The weight of the water in a cylinder is given
$\Rightarrow W = mg$
$ \Rightarrow W = \left( {\pi {r^2}h`} \right)\rho g$

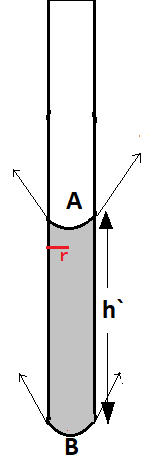
Now this total force will be supported by the total upward force
$
  \left( {\pi {r^2}h`} \right)\rho g = 2 \times 2\pi rT\cos \theta \\
   \Rightarrow h` = \dfrac{{4T\cos \theta }}{{r\rho g}} \\
 $
Now we have got both the heights
$\left( h \right)$due to immersion of capillary into the water and $\left( {h`} \right)$ after removing it from water
Hence,
$h = \dfrac{{2T\operatorname{Cos} \theta }}{{r\rho g}}$ $h` = \dfrac{{4T\cos \theta }}{{r\rho g}}$
Now divide
\[
\Rightarrow \dfrac{h}{{h`}} = \dfrac{{\left( {\dfrac{{2T\operatorname{Cos} \theta }}{{r\rho g}}} \right)}}{{\left( {\dfrac{{4T\cos \theta }}{{r\rho g}}} \right)}} \\
   \Rightarrow \dfrac{h}{{h`}} = \dfrac{1}{2} \\
   \Rightarrow h` = 2h \\
 \]
The new height after the removal of the tube from the water will be twice the precious height when the tube was dipped into the water.

Note: The pressure at any point inside the water is equal to all other points because of the surface tension water tends to acquire the smallest surface area this is the reason why water droplets are spherical. If the lower end of the tube is not covered then the water will move out when lifted.