
A body projected from the surface of the earth attains a height equal to the radius of the earth. The velocity with which the body was projected is
$\left( a \right)$ $\sqrt {\dfrac{{2GM}}{R}} $
$\left( b \right)$ $\sqrt {\dfrac{{GM}}{R}} $
$\left( c \right)$ $\sqrt {\dfrac{{3GM}}{R}} $
$\left( d \right)$ $\sqrt {\dfrac{{5GM}}{{4R}}} $
Answer
219.3k+ views
Hint Here in this question we have to find the velocity with which the body was projected and for this, we will use the conservation of energy and we know that the conservation of energy will be equal to energy at the earth's surface will be equal to the energy at the point at which the body will be after some velocity.
Formula used
Kinetic energy,
$K = \dfrac{1}{2}m{v^2}$
And potential energy,
$V = \dfrac{{ - GMm}}{R}$
Here,
$K$, will be the kinetic energy
$m$, will be the mass of the body
$v$, will be the velocity
$V$, will be the potential energy
$G$, will be the gravitational constant
$M$, will be the mass of the earth
$R$, will be the radius of the earth
Complete Step By Step Solution first of all we make the diagram to solve the question. So at the earth's surface, there is the body that is being projected from the earth’s surface. The body will cover the height which will be equal to the earth's radius.
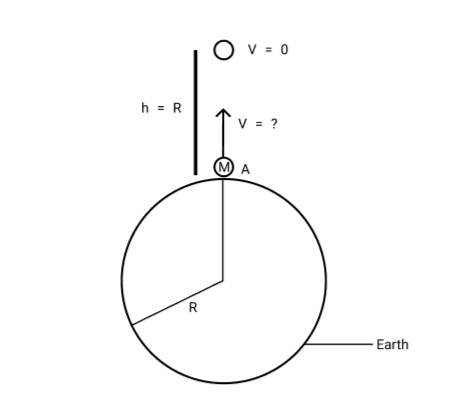
So from this, we can say that
$h = R$
Now by using the conservation of energy,
The energy at the point $A$will be equal to the energy at the point $B$
Therefore,
$K{E_A} + P{E_A} = K{E_B} + P{E_B}$
Now putting the value we know already from the formula, we get
Since at point $A$ the $PE$will be zero. And at height, $B$the kinetic energy will be zero.
Therefore,
$ \Rightarrow \dfrac{1}{2}m{v^2} + \dfrac{{ - GMm}}{R} = 0 - \dfrac{{GMm}}{{R + R}}$
Now, we will solve the above equation and we get
$ \Rightarrow \dfrac{1}{2}m{v^2} = \dfrac{{ - GMm}}{{2R}} + \dfrac{{GMm}}{R}$
On solving the RHS, we get
$ \Rightarrow \dfrac{1}{2}m{v^2} = \dfrac{{GMm}}{{2R}}$
Since $m$is common so it will cancel out, we have left
$ \Rightarrow {v^2} = \dfrac{{GM}}{R}$
Now, we will remove the root and we get
$ \Rightarrow v = \sqrt {\dfrac{{GM}}{R}} $
Therefore, the option $B$ will be correct.
Note So to understand the energy conservation we should have to be clear abo it. Energy conversion means to change its form, for example when supplied current to an electric motor then electric energy is converted into mechanical energy, and pumping of water takes place. Energy conservation means to conserve energy, for example, we switch off the bulb when it is not in use, so here electrical energy is conserved.
Formula used
Kinetic energy,
$K = \dfrac{1}{2}m{v^2}$
And potential energy,
$V = \dfrac{{ - GMm}}{R}$
Here,
$K$, will be the kinetic energy
$m$, will be the mass of the body
$v$, will be the velocity
$V$, will be the potential energy
$G$, will be the gravitational constant
$M$, will be the mass of the earth
$R$, will be the radius of the earth
Complete Step By Step Solution first of all we make the diagram to solve the question. So at the earth's surface, there is the body that is being projected from the earth’s surface. The body will cover the height which will be equal to the earth's radius.

So from this, we can say that
$h = R$
Now by using the conservation of energy,
The energy at the point $A$will be equal to the energy at the point $B$
Therefore,
$K{E_A} + P{E_A} = K{E_B} + P{E_B}$
Now putting the value we know already from the formula, we get
Since at point $A$ the $PE$will be zero. And at height, $B$the kinetic energy will be zero.
Therefore,
$ \Rightarrow \dfrac{1}{2}m{v^2} + \dfrac{{ - GMm}}{R} = 0 - \dfrac{{GMm}}{{R + R}}$
Now, we will solve the above equation and we get
$ \Rightarrow \dfrac{1}{2}m{v^2} = \dfrac{{ - GMm}}{{2R}} + \dfrac{{GMm}}{R}$
On solving the RHS, we get
$ \Rightarrow \dfrac{1}{2}m{v^2} = \dfrac{{GMm}}{{2R}}$
Since $m$is common so it will cancel out, we have left
$ \Rightarrow {v^2} = \dfrac{{GM}}{R}$
Now, we will remove the root and we get
$ \Rightarrow v = \sqrt {\dfrac{{GM}}{R}} $
Therefore, the option $B$ will be correct.
Note So to understand the energy conservation we should have to be clear abo it. Energy conversion means to change its form, for example when supplied current to an electric motor then electric energy is converted into mechanical energy, and pumping of water takes place. Energy conservation means to conserve energy, for example, we switch off the bulb when it is not in use, so here electrical energy is conserved.
Recently Updated Pages
Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Understanding Uniform Acceleration in Physics

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Understanding Atomic Structure for Beginners




