Question

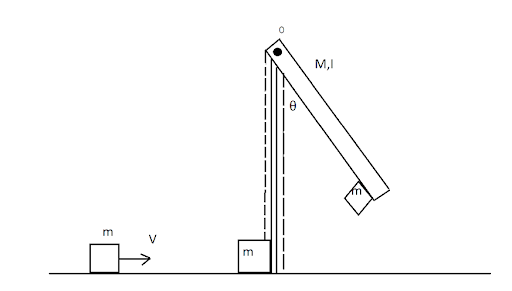
A block of mass \[m = 1\] kg slides with velocity \[v = 6\] m/s on a frictionless horizontal surface and collides with a uniform vertical rod and sticks to it as shown. The rod is pivoted about \[O\] and swings as a result of the collision making angle \[\theta \] before momentarily coming to rest. If the rod has mass \[M = 2\] kg, and length \[l = 1\] m, the value \[\theta \] of is approximately: (take \[g = 10\] $m/s^2$)


A. \[{49^\circ }\]
B. \[{55^\circ }\]
C. \[{63^\circ }\]
D. \[{69^\circ }\]

Answer 1

Hint: We are given a block of mass \[m = 1\]kg slides with velocity \[v = 6\] m/s on a frictionless horizontal surface and collides with a uniform vertical rod and sticks to it. Also, the rod of mass \[M = 2\] kg, and length \[l = 1\] m is pivoted about \[O\] and swings as a result of the collision making angle \[\theta \] before momentarily coming to rest. We have to find the approximate value of angle \[\theta \]. We will be using conservation of angular momentum to find out angular velocity \[\omega \] and conservation of energy to find the approximate value of angle \[\theta \].

Complete step by step solution:
By using conservation of angular momentum, we get
\[mvl = \dfrac{{M{l^2}}}{3}\omega + m{l^2}\omega \\ \Rightarrow mvl = \omega \left( {\dfrac{{M{l^2}}}{3} + m{l^2}} \right) \\ \]
On substituting the known values given in the question, we get
\[mvl = \omega \left( {\dfrac{{M{l^2}}}{3} + m{l^2}} \right) \\ \Rightarrow 1 \times 6 \times 1 = \omega \left( {\dfrac{{2 \times {1^2}}}{3} + 1 \times {1^2}} \right) \\ \Rightarrow 6 = \omega \left( {\dfrac{2}{3} + 1} \right) \\ \Rightarrow \omega = \dfrac{6}{{\left( {\dfrac{2}{3} + 1} \right)}} \\ \]
On further solving, we get
\[\omega = \dfrac{6}{{\dfrac{5}{3}}} \\
\Rightarrow \omega = \dfrac{{18}}{5} \\ \]
Now, on using conservation of energy, we get
\[\dfrac{1}{2}\left( {\dfrac{{M{l^2}}}{3}} \right){\omega ^2} + \dfrac{1}{2}\left( {m{l^2}} \right){\omega ^2} = (m + M){r_{cm}}(1 - \cos \theta ) \\ \Rightarrow \dfrac{1}{2}{l^2}{\omega ^2}\left( {\dfrac{M}{3} + m} \right) = (m + M)\left( {\dfrac{{ml + \dfrac{{Ml}}{2}}}{{m + M}}} \right)g(1 - \cos \theta ) \\ \Rightarrow \dfrac{1}{2} \times {1^2}{\left( {\dfrac{{18}}{5}} \right)^2}\left( {\dfrac{2}{3} + 1} \right) = (1 + 2)\left( {\dfrac{{1 + \dfrac{2}{2}}}{{1 + 2}}} \right)10(1 - \cos \theta ) \\ \Rightarrow \dfrac{5}{6} \times {\left( {\dfrac{{18}}{5}} \right)^2} = 3 \times \dfrac{2}{3} \times 10 \times (1 - \cos \theta ) \\ \]
On further solving, we get
\[\dfrac{5}{6} \times {\dfrac{{18}}{{{5^2}}}^2} = 20 \times (1 - \cos \theta ) \\ \Rightarrow \dfrac{{{{18}^2}}}{{30}} = 20 \times (1 - \cos \theta ) \\ \Rightarrow 1 - \cos \theta = \dfrac{{{{18}^2}}}{{30 \times 20}} = \dfrac{{27}}{{50}} \\ \]
On further solving, we get
\[\cos \theta = 1 - \dfrac{{27}}{{50}} \\ \Rightarrow \cos \theta = \dfrac{{23}}{{50}} \\ \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{{23}}{{50}}} \right) \\ \therefore \theta \approx {63^\circ } \]

Therefore the approximate value of \[\theta \] is \[{63^\circ }\].

Note: Students may make mistakes while calculating the value of angular velocity using conservation of angular momentum. They should define the terms in the equation of conservation of angular momentum as per their observations in the question. They should observe carefully and imagine the momentum of the rod and hence accordingly define the terms in the equation of conservation of angular momentum. Similar is the case with conservation of energy.