Question

A block of mass 1.9 kg is at rest at the edge of a table, of height 1 m. A bullet of mass 0.1 kg collides with the block and sticks to it. If the velocity of the bullet is 20 m/s in the horizontal direction just before the collision then the kinetic energy just before the combined system strikes the floor is (Take g = 10 m/\[{s^2}\]. Assume there is no rotational motion and loss of energy after the collision is negligible.)
A. 23 J
B. 21 J
C. 20 J
D. 19 J

Answer 1

Hint: When bullets get stuck to block, then total mass becomes the sum of both the mass of the block and the mass of the bullet. As a system there is no external force acting on it so momentum will be conserved. By using the conservation of linear momentum we can determine the velocity.

Formula used:
Linear momentum is given as,
\[p{\rm{ = m}} \times {\rm{v}}\]
Where $m$ is mass and $v$ is velocity of an object.
Work energy theorem is given as,
\[{W_{net}} = {K_f} - {K_i}\]
Where \[{W_{net}}\] is net work done, \[{K_f}\] is final kinetic energy and \[{K_i}\] is Initial kinetic energy.

Complete step by step solution:
Mass of a block, \[{m_1}\]= 1.9 kg
Height of a table, h= 1 m
Mass of a bullet, \[{m_2}\]= 0.1 kg
Velocity of the bullet is in the horizontal direction, v=20 m/s
Take g = 10 m/\[{s^2}\]

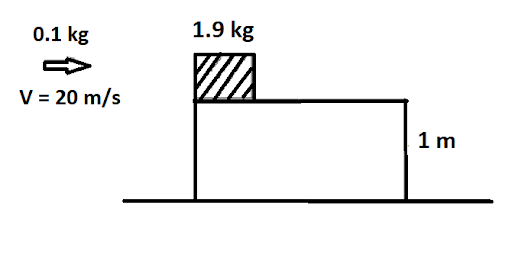
Image: A block is at rest at the edge of a table, of height 1 m and a bullet collides with the block and sticks to it.

As we know that momentum,
\[p = \text{mass} \times \text{velocity}\\
\Rightarrow p = m \times v\]
When bullets get stuck to the block, then total mass becomes \[{m_1} + {m_2} = 1.9 + 0.1 = 2{\rm{ kg}}\].

As system here no external force acting on it so momentum is conserved,
Initial momentum, \[{p_i}\]= Final momentum, \[{p_f}\]
Substituting the values,
\[0.1 \times 20 + 1.9 \times 0 = 2 \times v\]
Thus, the combined velocity is \[v = \dfrac{2}{2} = 1{\rm{ m/s}}\]

Let the final kinetic energy be K.
As work done due to gravity can be mgh=\[mg \times 1\]
Now by work energy theorem,
\[2 \times 10 \times 1 = K - \dfrac{1}{2} \times 2 \times {1^2}\]
\[\therefore K = 21{\rm{ J}}\]
Therefore, the kinetic energy at ground floor is \[K = 21{\rm{ J}}\].

Hence option B is the correct answer

Note: The work-energy theorem is defined as the net work done is equal to the change in kinetic energy. This theorem only applies to the network, not the work done by any single force. Also, the area under force and position graph gives the net work done.