Question

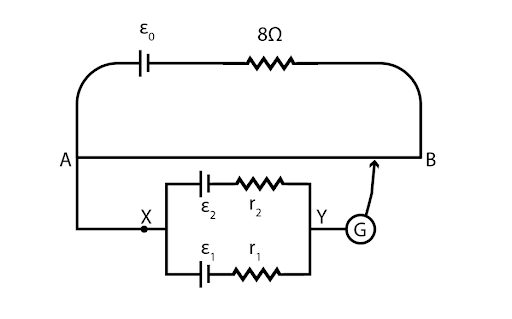
A battery of emf ${\varepsilon _0} = 6V$ is connected across a 2m long uniform wire having resistance $4\Omega /m$. The cell of small emf ${\varepsilon _1} = 2V$ and ${\varepsilon _2} = 3V$ having internal resistance $2\Omega $ and $1\Omega $ respectively are connected as shown in the figure. The null point will be obtained at

A. 0.10m
B. 0.25m
C. 0.50m
D. 0.75m

Answer 1

Hint:The problem is from the current electricity section of physics. We need to know the concepts of the potentiometer to solve this problem. Find the resistance and potential across AB. Then we have to find the potential gradient of AB. After that we have to find net emf from the emf’s ${\varepsilon _1}$ and ${\varepsilon _2}$. Once we find the net emf we can find the length.

Complete step by step solution:
The length of the wire AB = 2 m
Then the resistance of the wire AB = $4\Omega /m \times 2m = 8\Omega $
The potential gradient of wire AB, \[k = \dfrac{V}{L}\]
\[{\varepsilon _0} = i \times (8 + 8)\]
Where${\varepsilon _0} = 6V$and substitute the value in the equation and solve.
\[i = \dfrac{6}{{16}} = \dfrac{3}{8}A\]
Potential across AB, \[{V_{AB}} = i \times 8\Omega = \dfrac{3}{8} \times 8 = 3V\]
Potential gradient of AB, \[k = \dfrac{{{V_{AB}}}}{L} = \dfrac{{3V}}{{2m}} = \dfrac{3}{2}V{m^{ - 1}}\]
The net emf, \[\varepsilon = \dfrac{{\dfrac{{{\varepsilon _1}}}{{{r_1}}} - \dfrac{{{\varepsilon _2}}}{{{r_2}}}}}{{\dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}}}} = \dfrac{{\dfrac{2}{2} - \dfrac{3}{1}}}{{\dfrac{1}{2} + \dfrac{1}{1}}} = \dfrac{4}{3}V\]
The values given are, ${\varepsilon _1} = 2V$, ${\varepsilon _2} = 3V$, \[{r_1} = 2\Omega \], \[{r_2} = 1\Omega \].
If there is no deflection at the point. Then,
\[\varepsilon = kl\]
\[l = \dfrac{\varepsilon }{k} \\
\Rightarrow l = \dfrac{{\dfrac{4}{3}V}}{{\dfrac{3}{2}V{m^{ - 1}}}} \\
\Rightarrow l = \dfrac{4}{3} \times \dfrac{2}{3} \\
\Rightarrow l = \dfrac{8}{9} \\
\therefore l = 0.88\,m\]

Hence, the correct option is option D.

Additional Information: The potentiometer is a device used to measure an unknown voltage by comparing it to a known voltage. It can be used to compare the emf of several cells and to determine the emf and internal resistance of the specified cell.

The potentiometer's basic principle states that, if the wire has a uniform cross-sectional area and a uniform current flows through it, the potential drop across any part of the wire will be precisely proportional to the length of the wire.

The smallest change in the potential difference that a potentiometer can detect is its sensitivity. By lowering the potential gradient, the potentiometer's sensitivity can be improved. That is done by extending the potentiometer wire's length.

Note: The potentiometer's balancing point, also known as the null point, is the point on the sliding wire where the galvanometer indicates zero deflection. The balance point is used to determine the unknown voltage of the cell to which it is connected.