Question

A and B are moving in 2 circular orbits with angular velocity \[2\omega \] and \[\omega \] respectively. Their positions are shown at \[t = 0\]. Find the time when they will meet for the first time.

A. \[\dfrac{\pi }{{2\omega }}\]
B. \[\dfrac{{3\pi }}{{2\omega }}\]
C. \[\dfrac{\pi }{\omega }\]
D. They will never meet

Answer 1

Hint:When two objects move with different velocities, either angular velocities or linear velocities there is relative motion between them. In relative motion we assume either of the objects to be at rest and the other object is moving with respect to the first object. Then the problem gets reduced to a general kinematic problem.

Formula used:
\[\omega = \dfrac{{\Delta \theta }}{{\Delta t}}\],
Here \[\omega \] is the angular velocity, \[\Delta \theta \] is the angular displacement in time \[\Delta t\].

Complete step by step solution:
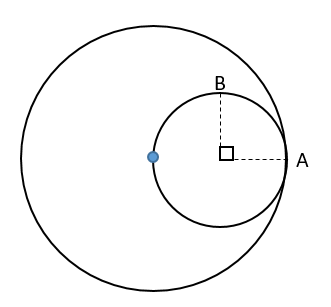
The angular velocities of A and B are given as \[2\omega \] and\[\omega \] respectively. We need to find the time when they meet for the first time. Let object A is at rest and B be moving with angular velocities.

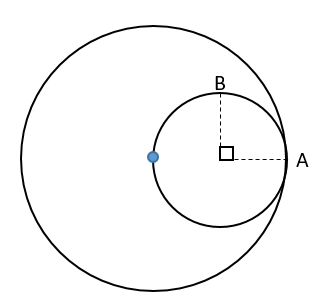
Image: The path of the motion of A and B

The relative angular velocity of B with respect A is,
\[{\omega _{BA}} = {\omega _B} \pm {\omega _A}\]

Case-1: when A and B are moving in the same direction.
\[{\omega _{BA}} = {\omega _B} - {\omega _A}\]
\[\Rightarrow {\omega _{BA}} = \omega - 2\omega \]
\[\Rightarrow {\omega _{BA}}= - \omega \]

The relative angular position of B with respect to A is,
\[{\theta _{BA}} = {\theta _B} - {\theta _A}\]
\[\Rightarrow {\theta _{BA}} = 0 - \dfrac{\pi }{2}\]
\[\Rightarrow {\theta _{BA}} = - \dfrac{\pi }{2}\]

B will meet A when it covers the initial angular separation between them.
So, the time taken to cover the initial angular separation is,
\[{t_1} = \dfrac{{{\theta _{BA}}}}{{{\omega _{BA}}}}\]
\[\Rightarrow {t_1} = \dfrac{{\left( { - \dfrac{\pi }{2}} \right)}}{{ - \omega }}\]
\[\Rightarrow {t_1} = \dfrac{\pi }{{2\omega }}\]

Case-2: when A and B are moving in opposite directions.
\[{\omega _{BA}} = {\omega _B} + {\omega _A}\]
\[\Rightarrow {\omega _{BA}} = \omega + 2\omega \]
\[\Rightarrow {\omega _{BA}} = 3\omega \]

The relative angular position of B with respect to A is,
\[{\theta _{BA}} = {\theta _B} - {\theta _A}\]
\[\Rightarrow {\theta _{BA}} = 0 - \dfrac{\pi }{2}\]
\[\Rightarrow {\theta _{BA}}= - \dfrac{\pi }{2}\]
B will meet A when it covers the initial angular separation between them.

So, the time taken to cover the initial angular separation is,
\[\begin{array}{c}{t_2} = \dfrac{{{\theta _{BA}}}}{{{\omega _{BA}}}}\\\end{array}\]
\[\Rightarrow {t_2}= \dfrac{{\left( { - \dfrac{\pi }{2}} \right)}}{{3\omega }}\]
\[\therefore {t_2}= \dfrac{\pi }{{6\omega }} \ldots \ldots \left[ {t > 0} \right]\]
Therefore, the correct option is A.

Note: Circular motion is defined as the movement of an item while spinning in a circle. Circular motion can be homogeneous or asymmetric. The angular rate of rotation and speed are constant in uniform circular motion, whereas the rate of rotation changes in non-uniform circular motion.