Question

A air bubble of radius 1 cm in water has an upward acceleration $9.8cm{s^{ - 2}}$. The density of water is $1gc{m^{ - 3}}$ and water offers negligible drag force on the bubble. The mass of the bubble is
(A) $1.52g$
(B) $4.51g$
(C) $3.15g$
(D) $4.15g$

Answer 1

Hint: In order to solve this question, we will balance all three forces acting on the air bubble which are gravity, upward force, and the buoyant force which acts in an upward direction, and then we will solve for the mass of the air bubble.

Formula used:
1. Force due to gravity on a body of mass m is:
$F = mg$
Where g is acceleration due to gravity $g = 980cm{s^{ - 2}}$
2. Force on a body of mass m and acceleration a is given by:
$F = ma$
3. The buoyant force on a body of volume V in water having density $\rho $ is:
$B = V\rho g$

Complete answer:

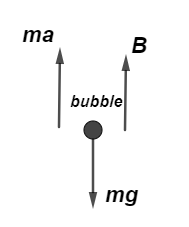
From the free body diagram of the air bubble we can see that by balancing all the three forces acting on the bubble, we get
$ma = B - mg \to (i)$

Now, volume of bubble is calculated as $V = \dfrac{4}{3}\pi {r^3}$ where $r = 1cm$
$V = \dfrac{4}{3}(3.14){(1)^3}$
$V = 4.19c{m^3} $
and density of water is given as $\rho = 1gc{m^{ - 3}}$

So, Buoyant force is given by $B = V\rho g$
$B = 4.19 \times 1 \times 980 $
$B = 4106.2gcm{s^{ - 2}} $

Now, due to upward acceleration force is $F = ma$ where $a = 9.8cm{s^{ - 2}}$
$F = 9.8m$ ‘m’ is the mass of the air bubble and force due to gravity on the bubble is given by $mg$ which is equal to $980m$

Using all the three forces values, put in equation (i) we get
$ 9.8m = 4106.2 - 980m$
$989.8m = 4106.2 $
$m = 4.15g $
So, the mass of the air bubble is $4.15g$

Hence, the correct option is (D) $4.15g$.

Note:It should be remembered that Archimedes found that when a body is immersed in water it experiences an upward force that is equal to the weight of the fluid displaced by the body and this force is known as buoyant force.