Question

A $12m$ long uniform bridge weighing $100000N$ is being supported at the two ends. A lorry weighing $30000N$ is parked at the $4m$ mark as shown in the figure. What are the forces acting on the bridge by support A and support B respectively?

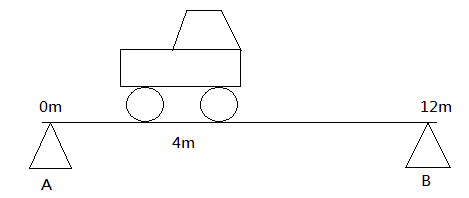
     Support A Support B
A) $70000N$ $60000N$
B) $60000N$ $70000N$
C) $65000N$ $65000N$
D) $90000N$ $40000N$

Answer 1

Hint: As the lorry is parked, the forces must be balanced. Balance the vertical and horizontal forces. Also, there will be torque acting on the lorry, balancing the torque from any force. There are four main forces acting in the system; reaction force from point A, reaction force from point B, gravitational force on lorry and gravitational force acting on the bridge.

Complete step by step solution:
Let us breakdown the problem and mention the given details first.
The length of the bridge is given as $l = 12m$ .
The force due gravity on bridge is ${F_{bridge}} = 100000N$
The force acting on the lorry is, it’s mass times the acceleration due to gravity which is given to be $30000N.$
Distance of lorry from point A ${d_A} = 4m$
As the lorry is parked and the system is not in motion, all the forces acting on the lorry and forces acting on the system must be balanced. Let’s mention the forces acting on the system:

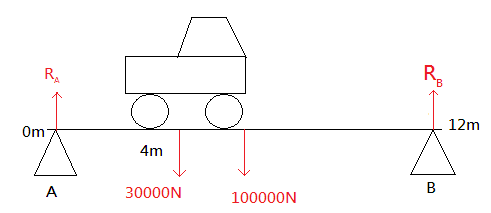
Here the reaction forces of A and B are in the upward direction while the forces acting on the lorry and bridge due gravity are in the downward direction. As there is no motion, so these forces must be balanced:
${R_A} + {R_B} = 30000N + 100000N$
$ \Rightarrow {R_A} + {R_B} = 130000N$
$ \Rightarrow {R_B} = 130000N - {R_A}$ --equation ($1$)
Torque will also work on the body. Torque is the force which can cause an object to rotate. There are four forces acting on the system. All four can bring about rotational motion. Let us consider the torque due reaction force at A:
We know that torque is calculated as the force acting multiplied by the perpendicular distance of the object. For point A, the force is acting in an upward direction and there are three points where this force will have effect.
1. At the centre of mass of the trolley
2. At the centre of mass of the bridge
3. At point B.

We need to find the perpendicular distances of all these three points with respect to point A.
1. Distance of lorry from point A ${d_A} = 4m.$
2. We know that the centre of mass acts at the centre of the body, so for the bridge the centre of mass will be at the geometrical centre which is at $6m$ from point A.
3. The distance of point B from point A is $12m.$
The direction of torque at centre of lorry and bridge will be in clockwise direction and the torque acting at point B is in anticlockwise direction. The direction of torque in this case, is in the same direction as the force acting. The torque acting in clockwise direction and anticlockwise direction must be balanced as there is no rotational motion:
$ \Rightarrow 30000N \times 4m + 100000N \times 6m = {R_B} \times 12m$
Substituting the value of ${R_B}$ from equation $1$ , we get
$ \Rightarrow 30000N \times 4m + 100000N \times 6m = \left( {130000N - {R_A}} \right) \times 12m$
$ \Rightarrow 120000 + 600000 = 1560000 - 12{R_A}$
$ \Rightarrow 12{R_A} = 1560000 - 720000$
Solving this we have
$ \Rightarrow 12{R_A} = 840000$
$$ \Rightarrow {R_A} = \frac{{840000}}{{12}}$$
$$ \Rightarrow {R_A} = 70000N$$
Therefore, the force acting at support A is $$70000N$$
From equation $1$ , we have
${R_B} = 130000N - {R_A}$
$ \Rightarrow {R_B} = 130000N - 70000N$
$ \Rightarrow {R_B} = 60000N$
The force acting at support B is $60000N$

This pair is option A, option A is the correct option.

Note: Remember that when the body is not in motion, then the forces acting on the body must be balanced. The force acting on the bridge was uniform; therefore, the force was acting at the centre of mass. Remember that when there is no rotational motion, then the torques must be balanced.