Question

A 100 W bulb $B_1$ and two 60 W bulbs $B_2$ and $B_3$, are connected to a 220 V source, as shown in Figure. Now $P_1$, $P_2$ and $P_3$ are the output powers of the bulbs $B_1$, $B_2$ and $B_3$ respectively. Then:

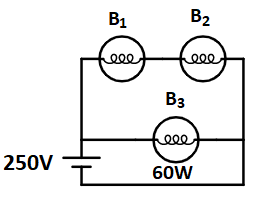
A) ${{{P}}_{{1}}}{{ > }}{{{P}}_{{2}}}{{ = }}{{{P}}_{{3}}}$
B) ${{{P}}_{{1}}}{{ > }}{{{P}}_{{2}}}{{ > }}{{{P}}_{{3}}}$
C) ${{{P}}_{{1}}}{{ < }}{{{P}}_{{2}}}{{ = }}{{{P}}_{{3}}}$
D) ${{{P}}_{{1}}}{{ < }}{{{P}}_{{2}}}{{ < }}{{{P}}_{{3}}}$

Answer 1

Hint: First of all find the resistance of the bulbs using formula, ${{R = }}\dfrac{{{{{V}}^{{2}}}}}{{{P}}}$. Then find out the value of current in the circuit using ohm’s law, ${{I = }}\dfrac{{{V}}}{{{R}}}$and then finally find out the value of power in bulbs using formula, ${{P = }}{{{I}}^{{2}}}{{R}}$. Finally evaluate the values of ${{{P}}_{{1}}}{{, }}{{{P}}_{{2}}}{{ and }}{{{P}}_{{3}}}$.

Complete step by step solution:
Given: Output power of bulb${{{B}}_{{1}}}$, ${{{P}}_1}{{ = 100 W}}$
Output power of bulbs ${{{B}}_2}$ and ${{{B}}_3}$, ${{{P}}_2}{{ = }}{{{P}}_3}{{ = 60 W}}$
Voltage V = 220 V
Formula for resistance is ${{R = }}\dfrac{{{{{V}}^{{2}}}}}{{{P}}}$
For bulb ${{{B}}_{{1}}}$, resistance is given by
$\Rightarrow {{{R}}_1}{{ = }}\dfrac{{{{{V}}^{{2}}}}}{{{{{P}}_1}}}$
Now substituting the values of V and ${{{P}}_{{1}}}$ in above equations, we get
$\Rightarrow {{{R}}_{{1}}}{{ = }}\dfrac{{{{22}}{{{0}}^{{2}}}}}{{{{100}}}}{{ = 484 \Omega }}$
For bulb ${{{B}}_2}$, resistance is given by
$\Rightarrow {{{R}}_2}{{ = }}\dfrac{{{{{V}}^{{2}}}}}{{{{{P}}_2}}}$
Now substituting the values of V and ${{{P}}_2}$ in above equations, we get
$\Rightarrow {{{R}}_2}{{ = }}\dfrac{{{{22}}{{{0}}^{{2}}}}}{{{{60}}}}{{ = 806}}{{.7 \Omega }}$
For bulb ${{{B}}_3}$, resistance is given by
$\Rightarrow {{{R}}_3}{{ = }}\dfrac{{{{{V}}^{{2}}}}}{{{{{P}}_3}}}$
Now substituting the values of V and ${{{P}}_3}$ in above equations, we get
$\Rightarrow {{{R}}_3}{{ = }}\dfrac{{{{22}}{{{0}}^{{2}}}}}{{{{60}}}}{{ = 806}}{{.7 \Omega }}$
Finding current in the circuit using ohm’s law
$
\Rightarrow {{V = IR}} \\
   \Rightarrow {{I = }}\dfrac{{{V}}}{{{R}}} $
Current in bulbs ${{{B}}_{{1}}}$ and ${{{B}}_2}$are same i.e. ${{{I}}_{{1}}}{{ = }}{{{I}}_{{2}}}{{ = }}\dfrac{{{{220}}}}{{{{{R}}_{{1}}}{{ + }}{{{R}}_{{2}}}}}{{ = }}\dfrac{{{{220}}}}{{{{484 + 806}}{{.7}}}}{{ = 0}}{{.170 A}}$
Current in bulb ${{{B}}_{{3}}}$ is given by
$\Rightarrow {{{I}}_3}{{ = }}\dfrac{{{V}}}{{{{{R}}_3}}}$
On substituting the values, we get
$\Rightarrow {{{I}}_3}{{ = }}\dfrac{{{{220}}}}{{{{806}}{{.3}}}}{{ = 0}}{{.272 A}}$
Formula for power in bulbs is given by
$\Rightarrow {{P = }}{{{I}}^{{2}}}{{R}}$
For bulb ${{{B}}_{{1}}}$, power is given by
$\Rightarrow {{{P}}_1}{{ = }}{{{I}}_1}^{{2}}{{{R}}_1}$
On substituting the values, we get
$\Rightarrow {{{P}}_{{1}}}{{ = (0}}{{.170}}{{{)}}^{{2}}}{{ \times 484 = 13}}{{.987 W}}$
For bulb ${{{B}}_2}$, power is given by
$\Rightarrow {{{P}}_2}{{ = }}{{{I}}_2}^{{2}}{{{R}}_2}$
On substituting the values, we get
$\Rightarrow {{{P}}_2}{{ = (0}}{{.170}}{{{)}}^{{2}}}{{ \times 806}}{{.7 = 23}}{{.313 W}}$
For bulb ${{{B}}_3}$, power is given by
$\Rightarrow {{{P}}_3}{{ = }}{{{I}}_3}^{{2}}{{{R}}_3}$
On substituting the values, we get
$\Rightarrow {{{P}}_3}{{ = (0}}{{.272}}{{{)}}^{{2}}}{{ \times 806}}{{.7 = 59}}{{.682 W}}$
Thus, ${{{P}}_{{1}}}{{ = 13}}{{.987 W, }}{{{P}}_{{2}}}{{ = 23}}{{.313 W and }}{{{P}}_{{3}}}{{ = 59}}{{.682 W}}$
So, ${{{P}}_{{1}}}{{ < }}{{{P}}_{{2}}}{{ < }}{{{P}}_{{3}}}$

Therefore, option (D) is the correct choice.

Note: A parallel circuit divides the current in various components and each component can draw current as per its appropriate operation or usage. Also, separation on/off switches can be put with each component in parallel combination. Total resistance in parallel combination decreases whereas in series combination increases.