JEE Chapter - Gaseous and Liquid States

In this chapter, we get to know the characteristics of gases and liquids, and on the basis of their characteristic, their behaviour at a given pressure, temperature for the given volume, and mass of gases and liquids. The reasons for the deviation of real gases from ideal gases and some properties of liquids and their applications.

This chapter is one of the easiest and the most significant chapters for competitive examinations like JEE, and this article will help you in mastering to score well in the exams.

Important Topics of Gaseous and Liquid States

• Gas Laws

• Ideal Gas Equation

• Derivation of Ideal Gas Equation

• Viscosity and Surface Tension

• Boyle's Law

• Charles Law

• Avogadro Law

• Gay Lussac's Law

Important Definitions of Gaseous and Liquid States

The Gaseous State

There are 118 elements in the periodic table of which 11 elements occur in the gaseous state under normal conditions; these elements are H, He, N, O, F, Ne, Cl, Ar, Kr, Xe, Rn. The intermolecular forces between molecules or atoms of the  gases are negligible due to this property of gas. The characteristics of gases are as follows:

• They are highly compressible.

• They have no fixed shape or volume.

• They exert pressure in all directions, equally.

• They spread evenly and completely in all proportions.

The properties of the gases are regulated by some laws which are discovered experimentally and these laws are collectively known as Gas Laws.

Gas Laws

There are four gas laws which are experimentally derived by studying the behaviour and properties of gases. These laws are named after the scientists who postulated them.

• Boyle’s Law: It gives the relationship between the pressure and volume of gases. This law states that at a given temperature, the pressure of a fixed amount of gas is inversely proportional to the volume of gas. 

P ∝ $\dfrac{1}{V}$

Or P V = constant

Or $\dfrac{P1}{P2}$ = $\dfrac{V1}{V2}$

• Charles' Law: It gives the relationship between temperature and volume of gas at a given pressure. This law states that the volume of a gas of fixed mass is directly proportional to the absolute temperature of the gas.

V ∝ T

Or $\dfrac{V}{T}$  = Constant

Or $\dfrac{V1}{T1}$ = $\dfrac{V2}{T2}$

• Gay-Lussac’s Law: It gives the relationship between the pressure and temperature. This law states that for fixed volume and mass of gas, pressure is directly proportional to absolute temperature.

P ∝ T

Or $\dfrac{P}{T}$  = Constant

Or $\dfrac{P1}{T1}$ = $\dfrac{P2}{T2}$

• Avogadro Law: This law states that at constant pressure and temperature, the volume of gas directly varies with the number of moles.

                                                               V ∝ n (moles of gas)                                                        

These gas laws give rise to the ideal gas equation and the gas which obeys all the gas laws or ideal gas equation is known as an ideal gas.

Ideal Gas Equation

The gas laws: Boyle’s Law, Charles’ law, and Avogadro Law are combined to give the ideal gas equation:

• Boyle's Law: P ∝ $\dfrac{1}{V}$ at constant T and n

• Charles Law: V ∝ T  at constant P and n

• Avogadro Law: V ∝ n at constant P and T

• Ideal Gas equation: V ∝ $\dfrac{nT}{P}$    

V = R $\dfrac{nT}{P}$   

PV = nRT

R is the proportionality constant known as universal gas constant.

Dalton’s Law of Partial Pressure

This law states that the pressure exerted by the unreactive gases is the sum of the partial pressure exerted by each gas.

• Ptotal = P1 + P2   + P3…….

• The partial pressure of each gas is the product of the mole fraction of that gas with the total pressure of the mixture of gas.

Ptotal = (n1 + n2 + n3 ) $\dfrac{RT}{V}$  

P1 / Ptotal = n1 / (n1 + n2 + n3 )

P1/ Ptotal = x1

P1 = x1 X Ptotal 

For ith gas:  Pi = xi X Ptotal 

• Pressure of dry gas can be calculated by subtracting the vapour pressure of water i.e. pressure exerted by the saturated water vapour from the total pressure of moist gas. The pressure exerted by water vapour is known as aqueous tension.

P dry gas = P moist gas  /total  - Aqueous tension

Kinetic Theory of Gases

Gases have negligible or no intermolecular forces and they move constantly in all directions. They collide with the wall of the container, as a result, the actual speed and the energy of the gas at a given time cannot be determined. 

The assumptions of the kinetic theory of gas are as follows:

• There is no interaction between the molecules of gases.

• The collision of gas molecules with the wall and with each other is an elastic collision.

• Kinetic energy and momentum is conserved. 

As the actual speed and energy of the gas cannot be determined, the kinetic energy of gases is referred to as the average kinetic energy of gases and it is given as

KE average = 3/2 kT, k is Boltzmann constant and k = R / NA

Boltzmann and maxwell distribution curve gave the speed of the gas at a given temperature as shown below:

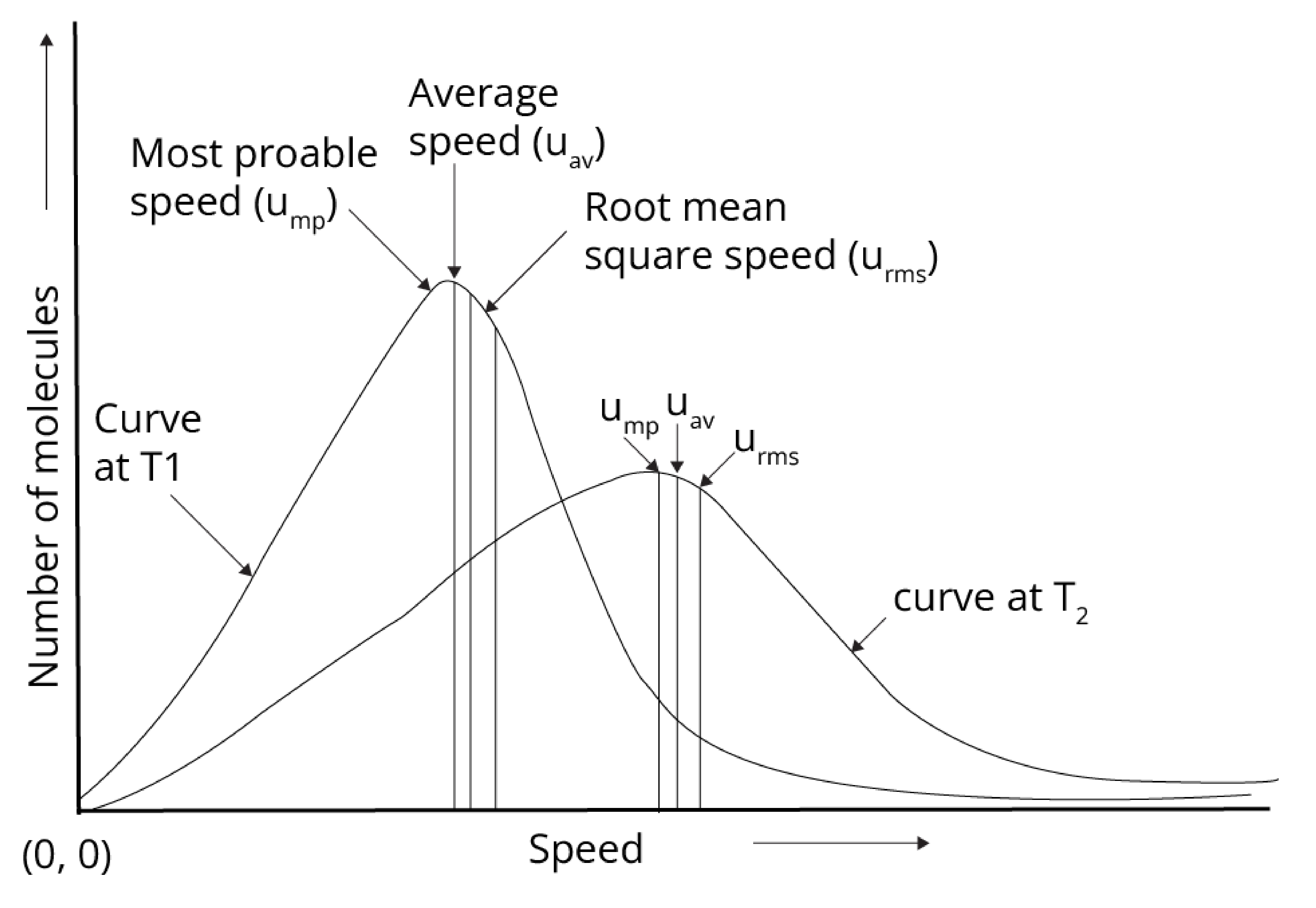
• Average speed (uav)   =   $\sqrt{ \dfrac {8RT}{\pi M}}$

• Root mean square speed (urms)   =   $\sqrt{ \dfrac {3RT}{M}}$

• Most probable speed (ump)  =  $\sqrt{ \dfrac {2RT}{M}}$

Order of speed:

                                  urms > uav  > ump

Real Gas Behaviour: Deviation from Ideal Gas Behaviour

We know that no gas is considered ideal gas, and there is a deviation in the behaviour of gases from the ideal gas behaviour. This deviation is seen from the graph of PV vs  V and P vs V graph as shown below:

(image Will be uploaded soon)

We know that the ideal gas equation is PV = nRT; so, the  pV / p must be constant and the line must be parallel to the p axis for ideal gas. The gases CO, CH4, H2 and He show deviation from the ideal gas behaviour.

(image Will be uploaded soon)

The graph shows that the real gas deviation from ideal gas and the real gas and ideal gas  intersect each other at low pressure. This deviation shows that the following assumptions made were not true:

• There is no interaction between the molecules of gases.

• The volume of gas is negligible instead of wide space.

The gases liquefy at high pressure and low temperature, this confirms that there is an interaction between the molecules of gases. Also, if the volume of gas is negligible, the pressure and volume graph of an ideal gas and real gas should have coincided.

At high pressure:

• The interaction of molecules of gas with each other is more than that of the wall of the container which leads to a decrease in the pressure of the gas. Thus, the pressure of the gas is lower than the pressure of the ideal gas by the given equation:

Pideal = Preal + an2/V2 

            where, ‘a’ is a constant

• The volume of gas also decreases, as at high pressure, the gases are restricted to the nb volume which is the total volume occupied by the gas. Therefore, the volume correction is : (V - nb), where b is a constant.

Now, by taking the correct pressure and volume into account for real gases, we get:

(P+ an2/V2) (V -nb)  =  nRT

This equation is known as the van der Waals equation where a and b are van der Waals constants.

Compressibility Factor

The deviation of real gas from ideal gas behaviour can be measured on the compressibility factor (Z) which is mathematical:

Z = ${ \dfrac {PV}{nRT}}$

For an ideal gas, Z = 1

(image Will be uploaded soon)

The compressibility factor for gases, visible from the graph, deviates from the ideal gas. At low pressure, the gases behave ideally and Z = 1;  at high pressure, the Z > 1 for the gases, showing deviation from ideal gas behaviour; also at moderate temperature, most of the gases have Z <1. 

Liquefaction of Gases

• Thomas Andrews plotted the isotherm of carbon dioxide at different constant temperatures. 

• He studied the pressure effect on the volume of carbon dioxide at a particular temperature.

• As the pressure decreases, the volume increases along the curve at a given temperature.  

• The area under the curve represents the gaseous and liquid carbon dioxide in equilibrium.

• Points like point A represent the gaseous state of carbon dioxide and the points like point D represent the liquified carbon dioxide.

• The temperature of 30.98 is the highest temperature at which carbon dioxide can exist in a liquid state. This temperature is known as critical temperature(Tc). Above the critical temperature, the gas cannot be liquified and exists in a gaseous state only.

• The volume of 1 mole of gas at critical temperature is known as critical volume. (Vc). The pressure at the critical temperature is known as critical pressure (Pc).

(image Will be uploaded soon)

The Liquid State

There are only 6 elements in the periodic table that exist in the liquid state. The molecules of liquid in the liquid state are closer and have stronger intermolecular forces than gases. The characteristics of liquids are as follows:

• They have fixed volume but not fixed shape.

• They can be compressed but pressure needs to be applied to compress them.

• Intermolecular forces between the molecules are more than gases.

• Liquids have more density than gases.

Vapour Pressure

• When the liquid is heated in a closed vessel, the liquid starts evaporating and the vapour of the liquid exerts pressure on the wall of the container. After some time, the pressure becomes constant and an equilibrium is established between the liquid and vapour phase. The pressure at this equilibrium stage is known as vapour pressure or equilibrium vapour pressure.

• The temperature at which the vapour pressure of a liquid becomes equal to the external pressure is known as the boiling point at that pressure.

• When the external pressure is 1 atm, then the boiling point is known as the normal boiling point.

• When the external pressure is 1 bar, then the boiling point is known as the standard boiling point.

Surface Tension

• The molecule on the surface of a liquid experiences a net downward force whereas the molecules in the bulk do not experience net force.

(image Will be uploaded soon)

• Due to the net attractive force on the surface molecule of the liquid, the surface molecules will try to minimise the surface area. Therefore, some liquids try to minimise surface tension and appear in a spherical shape (minimum surface area).

• The magnitude of surface tension depends on the intermolecular force of attraction.

• An increase in temperature increases the kinetic energy and thus decreases the intermolecular force of attraction, and hence, surface tension decreases. 

Viscosity

Viscosity is the characteristic of liquid to resist its tendency to flow, which is due to internal friction between the layers of liquid.

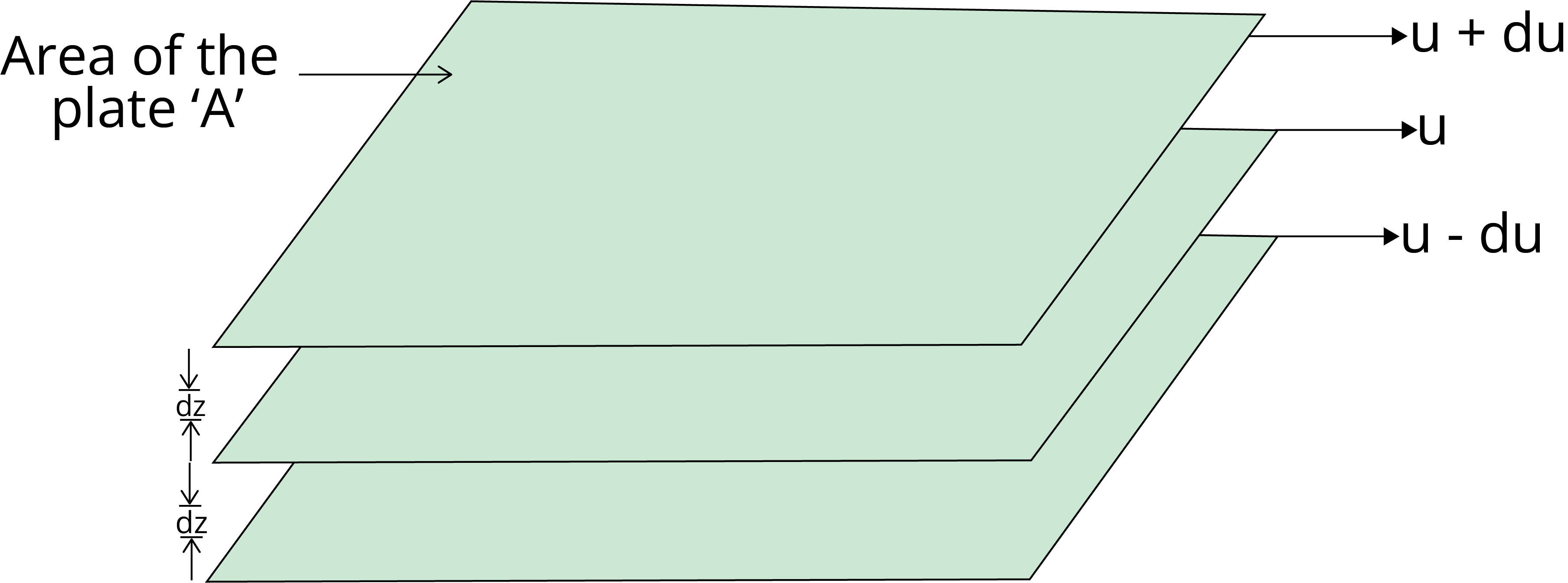
• The force required to maintain the flow of liquid and that force is proportional to the area and velocity gradient (du/dz).

F ∝ A

F ∝ (du/dz)

F = η A $\dfrac{du}{dz}$

where η is the proportionality constant and is known as the coefficient of viscosity.

Solved Examples from the Chapter

Example 1: The temperature at which oxygen molecules have the same root mean square speed as helium atoms have at 300 K is: 

(Atomic masses : He = 4 u, O = 16 u) 

• 1200 K

• 600 K

• 300 K

• 2400 K

Solution: (d) Given, atomic mass of He, M1 = 4 u

Atomic mass of O = 16 u

Molecular mass of O2, M2 = 32 u

T1 = 300 K

urms(He)   =   urms(O2)

$\sqrt{\dfrac{3R(T1)}{M1}}$  =  $\sqrt{\dfrac{3R(T2)}{M2}}$ 

${\dfrac{T1}{M1}}$   =    ${\dfrac{T2}{M2}}$

${\dfrac{300}{4}}$     =    ${\dfrac{T2}{32}}$   

T2 = 2400 K

Key points: The root mean square speed of the gas is given by     $\sqrt{\dfrac{3RT}{M}}$

Example 2: The initial volume of a gas cylinder is 750.0 ml. If the pressure of gas inside the cylinder changes from 840.0 mm Hg to 360.0 mm Hg, the final volume of gas will be:

1. 1.750 L

2. 7.50 L

3. 3.60 L

4. 4.032 L

Solution: (a) Given, initial volume, V1 = 750 ml

Initial pressure, P1 =  840.0 mm Hg

Final pressure, P2 =360 mm Hg

We know, P1 X V1 = P2  X V2

840 X 750  =   360  X V2

V2 =  1750 ml  =  1.750 L

Key points: According to Boyle’s Law,  P ∝ $\dfrac{1}{V}$ or  P V = constant

Solved Questions from the Previous Year Question Papers

Question 1: A mixture of one mole of H2, He, and O2 each are enclosed in a cylinder of volume V at temperature T. If the partial pressure of H2 is 2 atm, the total pressure of the gases in the cylinder is : 

1. 14 atm

2. 38 atm 

3. 6 atm

4. 22 atm

Solution: (b)  Given, n(H2)   =  1

n(He)  = 1

n(O2)  = 1

P(H2) = 2 atm

P(H2)  = x(H2)  X     Ptotal 

2  =  [n(H2)/ n(H2) +  n(He)  +  n(O2)]  X   Ptotal 

2  =  [1 / 1 +1+1]  X  Ptotal   =   [1/ 3]  X  Ptotal 

Ptotal =  2 X 3  =  6 atm

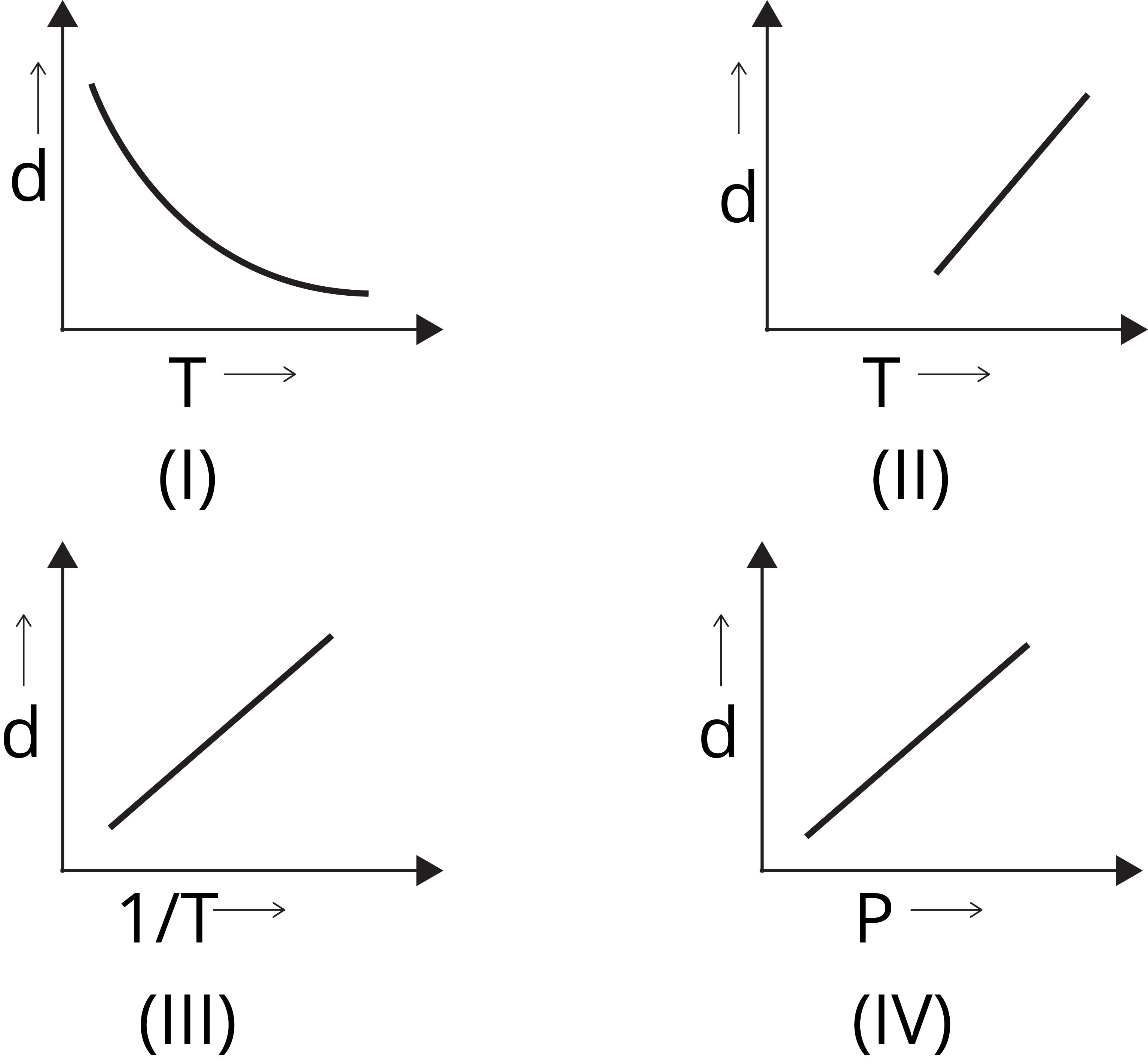
Question 2: Which one of the following graphs is not correct for ideal gas? 

1. II

2. III

3. I

4. IV

Solution: (a) We know,

d    =   M/V

For ideal gas, PV  =  nRT

Or PM =  dRT

d   ∝  1 /T   [∵ d vs  1/T will be a straight line and  

d vs  T will be a hyperbolic]

d   ∝   P      [∵ d vs  P will be a straight line]

Question 3: A pressure cooker reduces cooking time for food because

1. Heat is more evenly distributed in the cooking space. 

2. B.P of water involved in cooking is increased.

3. The higher pressure inside the cooker crushes the food.  

4. Cooking involves chemical changes helped by a rise in temperature. 

Solution: (b) The Gay Lussac's law states that constant pressure is directly proportional to the absolute temperature of the gas for a given mass of a gas. So on increasing pressure, temperature also increases. Hence, the boiling point of water is also increased in the pressure cooker.

Hence, option (2) is the answer. 

Practice Questions

Question 1: In the van der Waals equation of state of the gas law, the constant b is a measure of 

1. Intermolecular repulsions

2. Intermolecular attraction

3. Volume occupied by molecules

4. Intermolecular collisions per unit volume. 

Answer: (c) Volume occupied by molecules.

Question 2: The volume of gas A is twice that of gas B. The compressibility factor of gas A is twice that of gas B at the same temperature. The pressures of the gases for an equal number of moles are:  

1. 2PA = 3PB

2. 3PA = 2PB

3. PA = 3PB

4. PA = 2PB

Answer: (a)  2PA = 3PB

Conclusion

In this article, it is concluded that the gases have no fixed shape and volume and the weak intermolecular forces are present in the gases. The behaviour of gases is studied and the reason for the deviation in the behaviour of real gases from ideal gases is given. The gases can be compressed to be liquified by increasing the intermolecular forces.

The characteristics of liquid are that they have a moderate intermolecular force and fixed volume but not fixed shape. The properties of liquids such as viscosity, surface tension, and vapour pressure are also studied in this article which are important for the JEE competitive exams.