
A rectangle is constructed in the complex plane with its sides parallel to the axes and its center is situated at the origin. If one of the vertices of the rectangle is $a+ib\sqrt{3}$, then the area of the rectangle is
A. $ab\sqrt{3}$
B. $2ab\sqrt{3}$
C. $3ab\sqrt{3}$
D. $4ab\sqrt{3}$
Answer
228.3k+ views
Hint: In this question, we have to find the area of the given rectangle. Here the rectangle is constructed in such a way that, it is divided into four equal parts, and each part is another rectangle. So, the length and width of a rectangular part can able to find with the given details. In such a way we can calculate the area of the rectangle.
Formula Used: The complex number $(x,y)$ is represented by $x+iy$.
If $z=x+iy\in C$, then $x$ is called the real part and $y$ is called the imaginary part of $z$. These are represented by $\operatorname{Re}(z)$ and $\operatorname{Im}(z)$ respectively.
$z=x+iy$ be a complex number such that $\left| z \right|=r$ and $\theta $ be the amplitude of $z$. So, $\cos \theta =\dfrac{x}{r},\sin \theta =\dfrac{b}{r}$
And we can write the magnitude as
$\begin{align}
& \left| z \right|=\left| x+iy \right| \\
& \Rightarrow r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
\end{align}$
Thus, we can write
$z=x+iy=r\cos \theta +ir\sin \theta =r(\cos \theta +i\sin \theta )$
This is said to be the mod amplitude form or the polar form of $z$.
Where $\cos \theta +i\sin \theta $ is denoted by $cis\theta $ and the Euler’s formula is $\cos \theta +i\sin \theta ={{e}^{i\theta }}$
Complete step by step solution: Given that,
The rectangle is formed in such a way that its sides are parallel to the axes and the center of the rectangle is the origin.
The rectangle is as shown below:
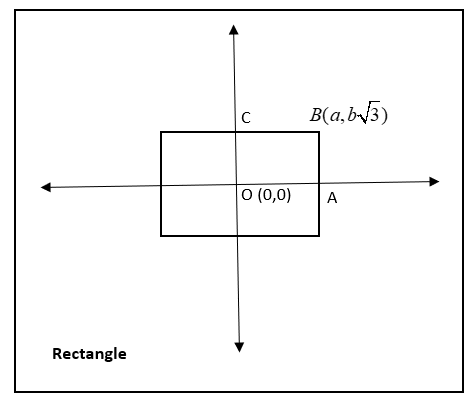
Consider the given coordinate as $B=(a,b\sqrt{3})=a+ib\sqrt{3}$
Then, the other vertices at one part of the rectangle are
$O(0,0);A(a,0);C(0,b\sqrt{3})$
Then the area of that part of the rectangle $(OABC)$ is
$\begin{align}
& Area=l\times b \\
& \text{ }=a\times b\sqrt{3} \\
& \text{ }=ab\sqrt{3} \\
\end{align}$
Thus, the area of the whole rectangle is
$\begin{align}
& =4\times Area(OABC) \\
& =4\times ab\sqrt{3} \\
& =4ab\sqrt{3} \\
\end{align}$
Option ‘D’ is correct
Note: Here we need to remember that the rectangle has its centre at the centre of the coordinate axes. So, we can able to calculate the area of one of the four parts of the rectangle.
Formula Used: The complex number $(x,y)$ is represented by $x+iy$.
If $z=x+iy\in C$, then $x$ is called the real part and $y$ is called the imaginary part of $z$. These are represented by $\operatorname{Re}(z)$ and $\operatorname{Im}(z)$ respectively.
$z=x+iy$ be a complex number such that $\left| z \right|=r$ and $\theta $ be the amplitude of $z$. So, $\cos \theta =\dfrac{x}{r},\sin \theta =\dfrac{b}{r}$
And we can write the magnitude as
$\begin{align}
& \left| z \right|=\left| x+iy \right| \\
& \Rightarrow r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
\end{align}$
Thus, we can write
$z=x+iy=r\cos \theta +ir\sin \theta =r(\cos \theta +i\sin \theta )$
This is said to be the mod amplitude form or the polar form of $z$.
Where $\cos \theta +i\sin \theta $ is denoted by $cis\theta $ and the Euler’s formula is $\cos \theta +i\sin \theta ={{e}^{i\theta }}$
Complete step by step solution: Given that,
The rectangle is formed in such a way that its sides are parallel to the axes and the center of the rectangle is the origin.
The rectangle is as shown below:

Consider the given coordinate as $B=(a,b\sqrt{3})=a+ib\sqrt{3}$
Then, the other vertices at one part of the rectangle are
$O(0,0);A(a,0);C(0,b\sqrt{3})$
Then the area of that part of the rectangle $(OABC)$ is
$\begin{align}
& Area=l\times b \\
& \text{ }=a\times b\sqrt{3} \\
& \text{ }=ab\sqrt{3} \\
\end{align}$
Thus, the area of the whole rectangle is
$\begin{align}
& =4\times Area(OABC) \\
& =4\times ab\sqrt{3} \\
& =4ab\sqrt{3} \\
\end{align}$
Option ‘D’ is correct
Note: Here we need to remember that the rectangle has its centre at the centre of the coordinate axes. So, we can able to calculate the area of one of the four parts of the rectangle.
Recently Updated Pages
If the points P1 and P2 represent two complex numbers class 11 maths JEE_Advanced

If R and C denote the set of real numbers and complex class 11 maths JEE_Advanced

If complex numbers z1 z2 and z3 represent the vertices class 11 maths JEE_Advanced

Let S be a set of all the distinct numbers of the form class 11 maths JEE_Advanced

Find how many numbers can be formed with the digits class 11 maths JEE_Advanced

The equation of the lines on which the perpendiculars class 11 maths JEE_Advanced

Trending doubts
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

JEE Advanced 2026 Revision Notes for Practical Organic Chemistry

IIT CSE Cutoff: Category‐Wise Opening and Closing Ranks

IIT Fees Structure 2025

Other Pages
JEE Main 2026: City Intimation Slip and Exam Dates Released, Application Form Closed, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

NCERT Solutions For Class 11 Maths Chapter 10 Conic Sections (2025-26)




