




How Does Torricelli's Theorem Apply to Fluid Flow Problems?
Torricellis Theorem is a vital principle in fluid mechanics describing the speed at which a liquid exits from an orifice below the surface of a tank. This concept is commonly encountered in competitive exams like JEE Main, and a solid understanding aids in mastering both theoretical and numerical questions about fluid flow. In this comprehensive article from Vedantu, you'll find explanations, derivation, images, and applications designed to clarify everything about torricelli's theorem.
Defining Torricelli’s Theorem: Statement and Formula
Torricelli’s theorem states that the speed (v) with which a liquid emerges from a small hole at depth h beneath an open liquid surface is equal to the velocity acquired by a body falling freely through the same vertical distance h under gravity. This direct relationship explains how gravity converts potential energy into kinetic energy for the fluid leaving the orifice.
In mathematical terms, torricelli's theorem formula is given by v = √(2gh), where v is efflux speed, g is acceleration due to gravity, and h is the vertical height of the liquid column above the orifice. This formula is crucial for JEE Main Physics, especially in questions about liquid flow and applications involving tanks and fountains.
Stepwise Derivation of Torricelli’s Theorem Using Bernoulli’s Principle
Let’s derive torricelli's theorem using Bernoulli’s equation, which connects pressure, velocity, and height in a steady incompressible flow. Consider a large tank filled with an incompressible liquid with a small orifice at depth h from the surface. Assume the tank is open to atmospheric pressure, and surface velocity is negligible because of the tank's large area.
Applying Bernoulli’s theorem to the liquid at the top surface (A) and just outside the orifice (B):
- At A (surface): Pressure = atmospheric, velocity ≈ 0, height = h
- At B (orifice): Pressure = atmospheric, velocity = v, height = 0
So, the Bernoulli equation becomes:
At A: Patm + ρgh + ½ρ(0)²
At B: Patm + ρg(0) + ½ρv²
Subtracting atmospheric pressure and rearranging gives ρgh = ½ρv². Simplifying, h = v²/(2g), which leads to v = √(2gh). Thus, torricelli's theorem derivation elegantly demonstrates the conversion of potential energy to kinetic energy as the fluid escapes.
Classic Setup: Torricelli’s Theorem Diagram and Experiment
Evangelista Torricelli validated this principle by creating a simple experiment: a vessel was filled with a liquid, and a small hole was made at depth h below the free surface. He measured the speed of the jet that escaped and compared it with the speed of a freely falling body dropped from height h. This classic illustration of torricelli’s experiment demonstrates the core concept for both practical demonstrations and physics exams.
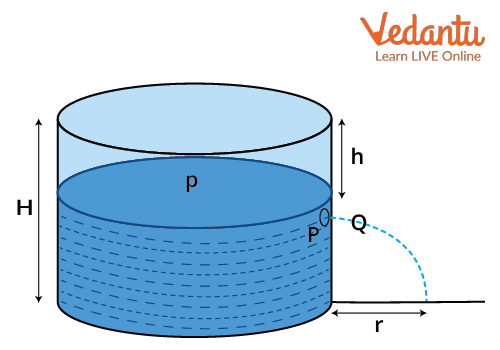
The experiment confirmed that both the liquid jet and free-falling object reach the same speed, backing up the theoretical approach of torricelli’s theorem proof. Modern science labs and engineering applications often refer to this diagram for clarity.
Physical Meaning, Units, and Key Parameters
Torricelli’s theorem class 11 physics questions often ask about the meaning of each variable in the formula. The table below provides a quick overview of symbols and units for reference in exams or practice:
| Symbol | Physical Quantity (SI Unit) |
|---|---|
| v | Speed of efflux (m/s) |
| g | Acceleration due to gravity (m/s²) |
| h | Vertical height of liquid (m) |
This formula assumes steady, non-viscous, incompressible flow and an orifice that opens directly into the atmosphere. The relation is used in designing spouts, fountains, and calibration of flow rates in many real-world devices.
Major Applications of Torricelli’s Theorem
The practical utility of torricelli's theorem application appears in questions about water tanks, spillways, and engineered hydraulic systems. Key uses include:
- Water jets and decorative fountains
- Calculation of flow speed in dams and spillways
- Laboratory fluid mechanics experiments
- Estimation of drainage speed from tanks
- Design of overflow pipes in reservoirs
- Predicting pipe discharge in irrigation and waste management
In engineering, fluid exit speed determines structural dimensions and efficiency. For further reading, the topic aligns well with Kinematics in Physics and other classical mechanics problems.
Comparing Torricelli’s Theorem with Bernoulli’s Theorem
Torricelli’s theorem in physics can be viewed as a special case derived from Bernoulli's theorem. While Bernoulli describes overall fluid flow energy, torricelli’s theorem focuses specifically on the efflux velocity from a stationary tank under gravity. The following table highlights their fundamental differences:
| Torricelli’s Theorem | Bernoulli’s Theorem |
|---|---|
| Speed from small opening in a tank | General energy balance along flow |
| Formula: v = √(2gh) | P + ½ρv² + ρgh = constant |
| Requires stationary liquid source | Valid for any streamline flow |
| Focuses on efflux/jets | Applies to all steady fluid situations |
In essence, use torricelli's theorem for questions about liquid jets and holes in tanks, and apply Bernoulli’s theorem for broader pressure–velocity puzzles in fluid mechanics.
Common Student Errors and Quick Tips
When working with torricelli's theorem class 11 physics or solving practice problems, candidates frequently commit certain mistakes. Be vigilant about these:
- Measuring slant height instead of vertical height h
- Neglecting fluid viscosity and compressibility
- Overlooking the velocity at surface when tank size isn’t large enough
- Incorrect unit conversion for g or h
- Confusing efflux velocity with projectile range
- Using theorem for gases (it applies only to incompressible fluids)
For advanced concepts, review connections with topics like Kinematic Equations and Work, Energy, and Power. These links deepen understanding of the physical meanings behind the theorem.
Significance of Torricelli’s Theorem in Exams
In JEE Main and similar competitive exams, questions around torricelli’s theorem pdf or analytical proof help bridge fluid statics and kinematics. Mastery allows students to quickly determine efflux speed, analyze reservoir problems, and even handle experimental arrangements found in real labs.
Torricelli's theorem also frequently appears alongside numericals on pressure difference, moment of inertia, and practical engineering applications. To fully grasp its scope, review its derivation, main assumptions, and variations for side and bottom orifices.
Torricelli’s Theorem in Hindi and Other Resources
For learners seeking regional resources, torricelli's theorem in hindi guides and videos are also widely available to supplement English notes. These help break down the core concepts, ensuring accessibility for all students preparing for engineering entrance exams.
A focused review of torricelli’s theorem definition, its applications, and the clear stepwise proof enables the efficient solution of related physics problems. Incorporate this knowledge into regular revision to guarantee success in your upcoming examinations with Vedantu support.
FAQs on Understanding Torricelli's Theorem in Fluid Dynamics
1. What is Torricelli's theorem?
Torricelli's theorem states that the speed of efflux of a liquid under gravity through an orifice at the bottom of a tank is equivalent to the velocity acquired by a body falling freely from the same height.
Key points:
- The formula is: v = √(2gh), where v is speed, g is acceleration due to gravity, and h is the liquid column height above the orifice.
- It applies to large tanks with small orifices.
- It helps in calculating fluid discharge rates and is vital in physics and engineering syllabi.
2. State Torricelli's theorem with mathematical expression.
Torricelli's theorem mathematically expresses the velocity of liquid flowing from an orifice under gravity.
Mathematical expression:
- v = √(2gh)
- Where v is efflux velocity, g is acceleration due to gravity, and h is the liquid height.
3. What are the applications of Torricelli's theorem?
Torricelli's theorem is widely used in real-world and exam scenarios for fluid dynamics.
Common applications:
- Designing water tanks and dams
- Predicting efflux rates in hydraulic systems
- Measuring flow rates in laboratory experiments
- Engineering studies of fluid discharge
- CBSE and competitive exam questions on practical physics
4. Who discovered Torricelli's theorem?
Torricelli's theorem was discovered by Evangelista Torricelli, an Italian physicist and mathematician, in the 17th century.
Key facts:
- Torricelli made significant contributions to fluid mechanics.
- He is also known for inventing the barometer.
5. What assumptions are made in Torricelli's theorem?
Torricelli's theorem is based on certain ideal assumptions.
Key assumptions include:
- The liquid is non-viscous and incompressible.
- Flow is steady and the velocity at the surface of the tank is negligible.
- The orifice is small compared to the tank's size.
- Liquid level remains constant during discharge.
6. How do you derive Torricelli's theorem?
Torricelli's theorem is derived using the principle of conservation of energy for fluids.
Derivation steps:
- Consider a liquid at height h from the orifice.
- Potential energy lost is converted to kinetic energy.
- Set mgh = (1/2)mv² and solve for v to get v = √(2gh).
7. What is the significance of Torricelli's theorem in fluid mechanics?
Torricelli’s theorem provides a quick calculation for predicting the speed of liquid leaving a hole, essential in engineering and physics.
Importance:
- Helps design safe and efficient hydraulic systems.
- Enables accurate determination of flow rates.
- Forms a basis for further experiments in fluid dynamics.
8. What factors affect the velocity according to Torricelli's theorem?
The velocity of efflux in Torricelli's theorem is influenced by:
- The height (h) of the liquid column above the orifice.
- The value of gravitational acceleration (g).
9. How does Torricelli's theorem relate to Bernoulli's principle?
Torricelli’s theorem is a special case of Bernoulli’s principle applied to fluids at rest and in motion.
Relationship:
- Derives efflux speed by equating potential energy and kinetic energy, as Bernoulli’s equation does for fluid flows.
- It assumes zero velocity at the liquid surface and atmospheric pressure at both surface and orifice.
10. Why is the velocity at the surface of the liquid neglected in Torricelli's theorem?
The velocity at the surface is considered negligible in Torricelli's theorem because the area of the tank surface is much larger than the area of the orifice.
As a result:
- The liquid descends very slowly at the surface compared to its speed at the orifice.
- This simplifies calculations and aligns with CBSE exam assumptions.
























