




How Do Spring Block Oscillations Work? Principles, Equations & Real-Life Examples
Spring block oscillations illustrate how restoring forces drive simple harmonic motion, a core concept for both JEE and NEET aspirants.
The spring-block system helps visualize the balance between force and motion, essential in understanding oscillatory phenomena deeply.
What Is Spring Block Oscillation?
A spring block oscillator consists of a mass attached to a spring, moving back and forth due to the spring’s restoring force. This movement exemplifies simple harmonic motion, which is pivotal in many oscillatory systems.
When displaced, the spring exerts a restoring force proportional to the displacement, pulling the block towards equilibrium and triggering repetitive motion.
Real-Life Visualization and Analogy
Imagine a child bouncing on a trampoline. As the trampoline stretches and compresses, the child oscillates up and down, resembling spring-block dynamics clearly.
Engineers use spring oscillations in car suspensions to absorb shocks, ensuring smooth rides by managing energy between components in motion.
Spring Block System Components
The essential elements in a spring-block setup are the mass (block) and the spring with its constant $k$. Varying these factors tunes the oscillation characteristics.
- Block or mass (m)
- Spring constant (k)
- Equilibrium position
- Displacement (x or y)
- External force (if any)
Types of Spring Block Arrangements
Spring block systems can be arranged in several ways, each affecting oscillation properties and applications in physics or engineering contexts.
- Horizontal Block-Spring System
- Vertical Block-Spring System
- Block connected to springs in series
- Block in between two springs
- Block connected to springs in parallel
Physics Behind Spring Oscillation
When displaced by $x$, a spring exerts $F = -k x$, consistent with Hooke's law. This restoring force underpins the simple harmonic motion observed in the system.
The inertia of the block and the elasticity of the spring combine, resulting in oscillations whose characteristics depend on the mass and spring constant exclusively.
Mathematical Model and Core Formulas
The motion is described by $m \dfrac{d^2x}{dt^2} = -k x$. The general solution—$x(t) = A \cos(\omega t + \phi)$—captures displacement as a function of time.
Angular frequency is $\omega = \sqrt{\dfrac{k}{m}}$, and the period of oscillation becomes $T = 2\pi \sqrt{\dfrac{m}{k}}$—both vital for JEE problem-solving.
| Parameter | Expression |
|---|---|
| Restoring Force | $F = -k x$ |
| Angular Frequency | $\omega = \sqrt{\dfrac{k}{m}}$ |
| Time Period | $T = 2\pi \sqrt{\dfrac{m}{k}}$ |
| Max. Acceleration | $a_{max} = \omega^2 A$ |
Horizontal Block-Spring System Explained
In a frictionless, horizontal setup, only the spring’s force governs the block’s oscillation, making it ideal for applying core SHM formulas directly.
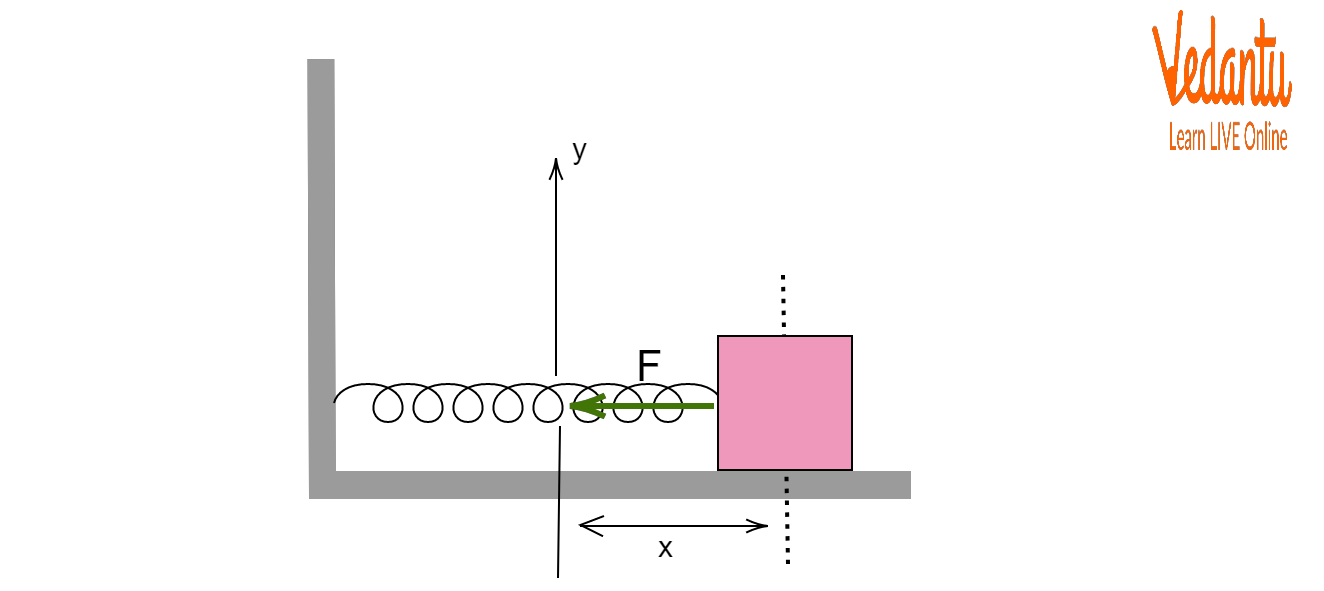
Energy transforms continuously between kinetic and potential forms, peaking alternately as the block moves through equilibrium and extreme points.
A deep understanding of such models is further discussed in our Spring Mass System Overview.
Vertical Block-Spring System (Gravity Influence)
In the vertical system, gravity stretches the spring, shifting the equilibrium. The block oscillates about this new position, with gravity’s effect cancelling out in the equations of motion for oscillations.
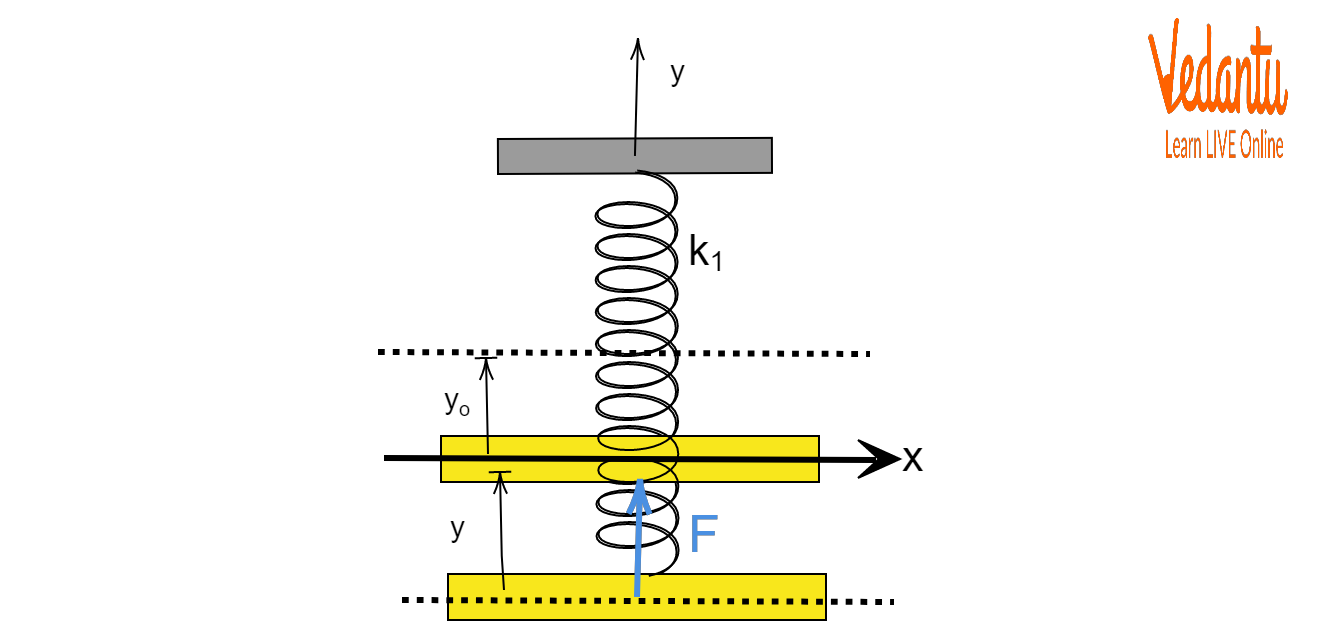
The time period remains $T = 2\pi \sqrt{\dfrac{m}{k}}$, showing the independence of period from gravitational acceleration and amplitude.
Related phenomena are explained in detail under Understanding Simple Harmonic Motion.
Springs Connected in Series and Parallel
Spring systems often feature multiple springs. Their combination alters the net spring constant, directly impacting oscillation frequency and period.
For series: $k_{net} = \dfrac{k_1 k_2}{k_1 + k_2}$. For parallel: $k_{net} = k_1 + k_2$, both modifying the effective stiffness experienced by the block.
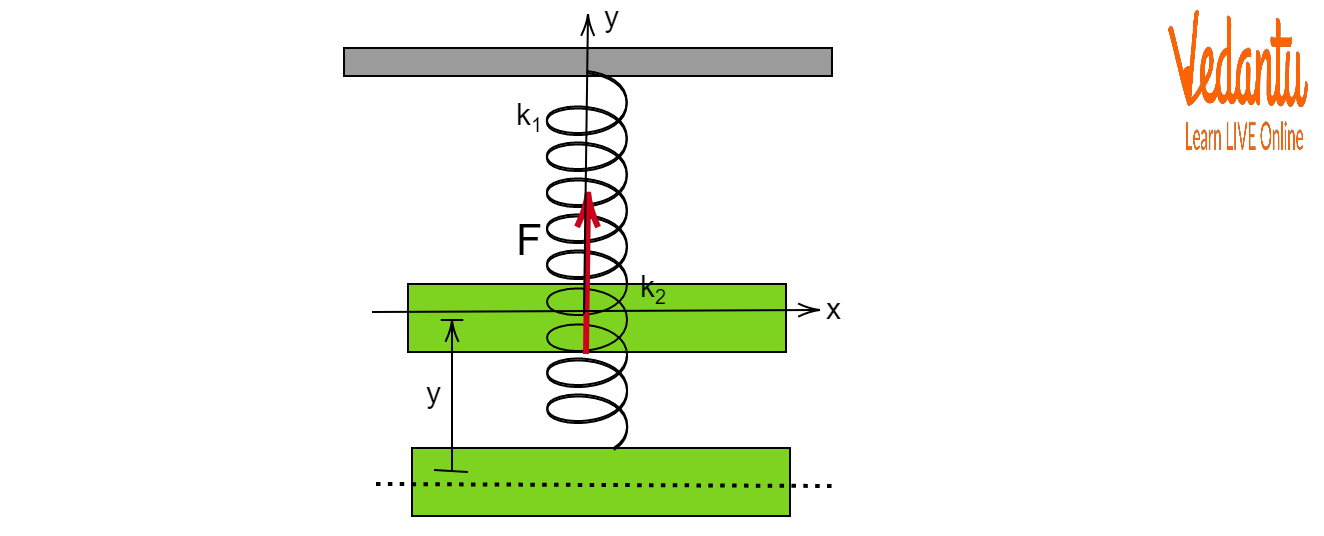
In series, the effective spring constant is reduced, leading to slower oscillations and longer periods than a single spring.
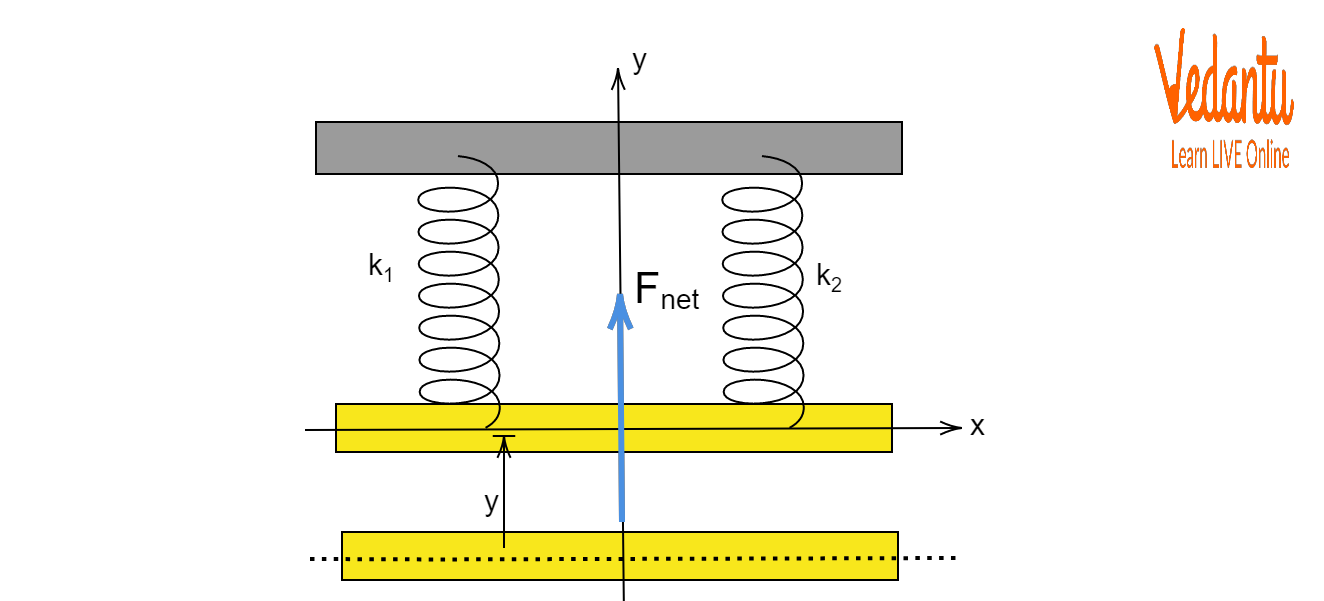
In parallel, the system stiffens, raising frequency and cutting the period—that's crucial for designing responsive mechanical systems and for JEE questions.
Compare energies in these systems via our guide on Elastic Potential Energy in Springs.
Block Placed Between Two Springs
Placing a block between two oppositely attached springs means both provide restoring forces when the block is displaced, so net force is $F = -(k_1+k_2) x$.
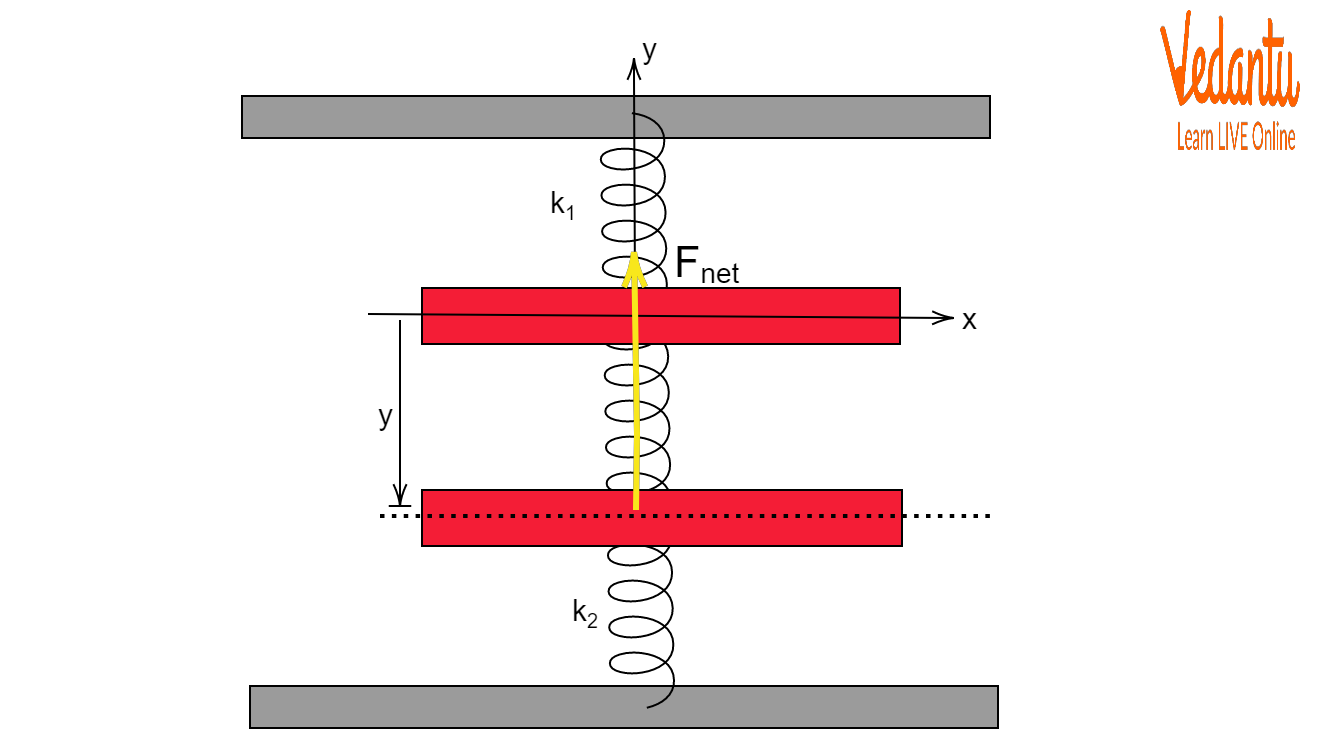
This modifies the angular frequency: $\omega = \sqrt{\dfrac{k_1+k_2}{m}}$. The arrangement is common in seismic vibration dampers.
Period and Frequency of Spring Oscillation
The period of spring oscillation tells us the time for one complete cycle. It depends only on $m$ and $k$, not on amplitude or a constant force like gravity.
For JEE, recall: $T = 2\pi \sqrt{\dfrac{m}{k}}$ and $f = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}}$, embedding the essence of Overview of Oscillations and Waves.
Energy in Spring Block Oscillations
Total mechanical energy in the system remains constant, continuously transforming between kinetic ($\dfrac{1}{2} m v^2$) and potential ($\dfrac{1}{2} k x^2$) energy.
At mean position: kinetic energy is maximum, potential energy is zero; at extreme: kinetic energy is zero, potential energy is maximum.
Solved Example: Standard JEE Problem
A $2\,kg$ block attached to a $k = 50$ N/m horizontal spring oscillates on a smooth surface. Find the period of oscillation.
Solution: $T = 2\pi \sqrt{\dfrac{2}{50}} = 2\pi \sqrt{0.04} = 2\pi \times 0.2 \approx 1.26$ seconds. Key formulae: $T = 2\pi \sqrt{\dfrac{m}{k}}$.
Practice Question
If a mass $m$ is attached between two springs with constants $k_1 = 100$ N/m and $k_2 = 200$ N/m, what is the frequency of its oscillation?
Diagrammatic View Explained
The displacement vs. time graph for spring-block oscillation shows a pure sinusoidal wave, highlighting the constant amplitude and fixed period seen in SHM.
Understanding such graphs is vital for analyzing system responses, mechanical stability, and rapid problem assessment in exams.
Common Mistakes and JEE Tips
Students often misapply formulas, especially when gravity is present, and forget period independence from amplitude or constant forces.
- Always use effective spring constant for series/parallel setups
- Ignore amplitude for calculating period
- Check if question demands energy or time period
Details about differences in work and energy approaches can be studied in Difference Between Work and Energy.
Power analysis questions, sometimes seen in oscillatory problems, are clarified at Work, Energy, and Power Explained.
Key Related Topics for Mastery
- Simple Harmonic Motion
- Energy Conservation in Oscillation
- Damped and Forced Vibrations
- Resonance and Phase Difference
- Wave Motion and Superposition Principle
- Elastic Properties of Materials
FAQs on Understanding Spring Block Oscillations in Physics
1. What is a spring block oscillator?
A spring block oscillator is a simple mechanical system where a block attached to a spring oscillates back and forth when displaced from its equilibrium position. Key features include:
- It demonstrates simple harmonic motion (SHM).
- The restoring force is provided by the spring according to Hooke's Law.
- Commonly used to illustrate SHM concepts in physics and examinations.
2. What are the key formulas for spring block oscillations?
The essential formulas for a spring block oscillator involve force, acceleration, frequency, and energy. Important equations:
- Restoring force: F = -kx
- Time period: T = 2π√(m/k)
- Frequency: f = 1/T
- Maximum speed: v_{max} = Aω
- Total energy: E = (1/2)kA^2
3. What is the time period of a mass attached to a spring?
The time period (T) of oscillation for a mass-spring system depends on the mass (m) and the spring constant (k):
- T = 2π√(m/k)
- Increasing mass increases time period.
- Stiffer springs (higher k) decrease time period.
4. What is meant by simple harmonic motion in the context of spring oscillations?
In a spring block system, simple harmonic motion (SHM) refers to periodic motion where the restoring force is directly proportional to displacement but acts in the opposite direction. Key points:
- Obeys Hooke’s Law: F = -kx
- Motion is sinusoidal and repeats at regular intervals
- Occurs when the block oscillates around the equilibrium point
5. How does damping affect spring block oscillations?
Damping refers to the reduction in amplitude of oscillations due to energy loss (often from friction or air resistance). Its effects include:
- Gradual decrease in oscillation amplitude over time
- Decrease in total energy of the system
- Eventually stops the motion if damping is strong
6. Explain the principle of conservation of energy in a spring block oscillator.
In a spring block oscillator, the total mechanical energy remains constant, alternating between kinetic and potential forms:
- Potential energy is stored when the spring is compressed or stretched.
- Kinetic energy is maximum when the block passes equilibrium.
- Total energy: E = (1/2)kA^2 (in the absence of damping)
7. What factors affect the frequency of oscillation of a spring block system?
The frequency of oscillation (f) depends mainly on two factors:
- Mass of the block (m) – increased mass lowers frequency
- Spring constant (k) – stiffer springs give higher frequency
- Formula: f = (1/2π)√(k/m)
8. Differentiate between free and forced oscillations in a spring block system.
Free oscillations occur when the block moves under its own restoring force; forced oscillations happen when an external force is periodically applied.
- Free: No external force after initial push or release, natural frequency observed
- Forced: Continuous periodic driving force, possible resonance
- Both demonstrate key principles of oscillatory motion
9. State Hooke’s Law and its significance in spring block oscillations.
Hooke’s Law states that the force exerted by a spring is proportional to its extension or compression, given by F = -kx. Its significance includes:
- Foundation for understanding spring block oscillations
- Explains restoring force causing simple harmonic motion
- Helps derive time period and frequency formulas
10. What is the phase and amplitude in spring block oscillations?
In spring block oscillators, amplitude (A) is the maximum displacement from equilibrium, while phase (φ) indicates the current state within the oscillation cycle. Key points:
- Amplitude determines energy and maximum speed
- Phase specifies position at a given time, measured in radians or degrees
- Both used for describing and solving oscillation problems


































