




How Does a Solenoid Produce a Magnetic Field?
A solenoid produces a controlled magnetic field using current-carrying coils—essential for electromagnetism and JEE/NEET Physics. Master its reasoning to excel in exams.
A solenoid is essentially a long, tightly wound helical coil of wire that generates a nearly uniform magnetic field when electric current flows through it.
You can visualize the solenoid like a stack of closely arranged loops, similar to the spring in a pen, each loop enhancing the overall magnetic field inside.
What is a Solenoid?
A solenoid consists of copper wire wound over a cylindrical core—air or soft iron—creating overlapping magnetic fields from each turn.
The net field results from the vector addition of fields produced by individual turns, yielding uniformity if the coil is long and tightly wound.
Such arrangement is vital to topics like Magnetic Effects Of Current due to its practical field distribution.
Magnetic Field Lines and Direction in a Solenoid
The magnetic field lines inside a solenoid are parallel to the axis, showing a uniform and strong internal magnetic field.
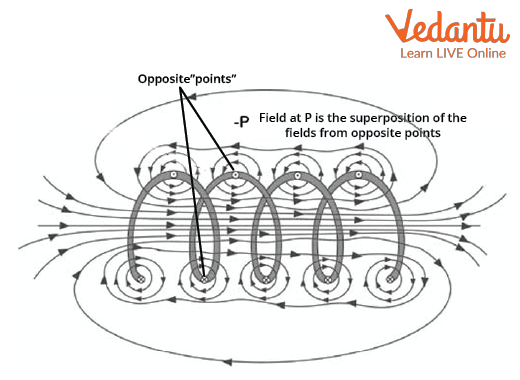
Outside the solenoid, these lines spread out, with the external field nearly negligible, especially for a long solenoid, thanks to symmetry and superposition.
Following the right-hand thumb rule, point your thumb in the current’s direction, and your curled fingers represent the magnetic field loops around the wire.
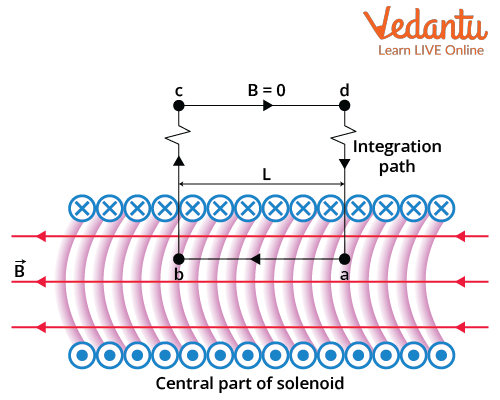
This directional attribute means the solenoid acts as a bar magnet, with distinguishable north and south poles at its ends.
Magnetic Field Outside a Solenoid
For an ideal, infinitely long solenoid, the external magnetic field cancels out, resulting in almost zero field outside.
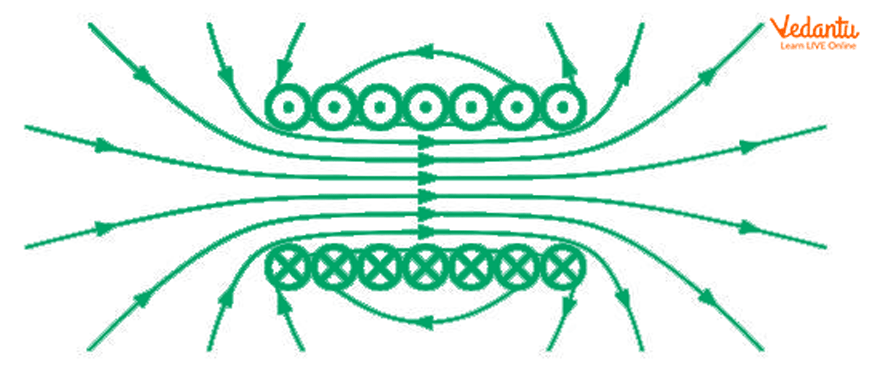
In practice, the external volume is much larger, so the sparse field lines make the outside field negligible compared to the interior.
This characteristic allows solenoids to focus fields inside, ideal for applications like electromagnets and MRI machines.
Understanding this contrast is crucial when moving to topics like Self Inductance in electromagnetic systems.
Solenoid Magnetic Field Formula and Derivation
Inside a long solenoid, the magnetic field $B$ is given by Ampère’s Law: $B = \mu_{0} n I$, where $n$ is the number of turns per unit length and $I$ is the current.
Here, $\mu_{0}$ is the permeability of free space ($4\pi \times 10^{-7}\ \text{T m/A}$), showing the strength of the medium supporting magnetic field lines.
With a ferromagnetic core, we include relative permeability $\mu_{r}$: $B = \mu_{0} \mu_{r} n I$, enhancing the field inside the solenoid.
For exam questions, it's key to recall that the formula is independent of the solenoid’s radius—dimension only influences fringe effects, not internal uniformity.
This powerful internal magnetic control forms the foundation of Solenoid Magnetic Field calculations and engineering applications.
| Parameter | Relationship |
|---|---|
| Number of Turns (N) | $B \propto N$ |
| Current (I) | $B \propto I$ |
| Core Permeability | $B \propto \mu_{r}$ |
| Length of Solenoid (l) | $B \propto \dfrac{N}{l}$ |
Solenoid Magnetic Field: Real-Life Applications and Visualization
Solenoids serve in devices like relays, speakers, and MRI machines, where controlled, strong magnetic fields are essential for precise operation.
- Core element in electromagnets and electric bells
- Widely used in magnetic resonance imaging (MRI) scanners
- Fundamental for inductors, transformers, and electric relays
- Employed for experimental demonstration of magnetic fields
Visualize the solenoid as a ‘magnetic pipe’ where field lines flow densely in the center, remaining parallel, like water streaming through a hose.
This imagery clarifies why the field remains uniform inside and negligible outside for a long solenoid, critical for accurate measurements in lab setups.
Such uniformity is compared with the more divergent field of a loop or a straight wire—covered in Mutual Inductance discussions.
Solved Numerical Example: JEE-Style
A solenoid has 200 turns, length $0.2$ m, and carries a $4\,A$ current. Calculate the magnetic field inside.
Number of turns per unit length: $n = \dfrac{200}{0.2} = 1000\, \text{turns/m}$
Using the formula: $B = \mu_{0} n I = 4\pi \times 10^{-7} \times 1000 \times 4 = 5.03 \times 10^{-3}\,T$
Practice Question
If a solenoid has 500 turns over $0.5$ m carrying $2\,A$, what is the field inside?
JEE Relevance and Common Mistakes
JEE often tests understanding of ideal solenoids, field direction, and how adding a core affects field strength—concepts directly asked in multiple-choice and numerical questions.
- Confusing uniform field inside with field outside
- Using incorrect value for number of turns per unit length
- Forgetting to include core permeability
Related Topics for Further Exploration
- Bar magnet and magnetic field similarities
- Biot-Savart law for current loops
- Electromagnetic induction principles
- Magnetic materials and permeability
FAQs on Understanding the Magnetic Field of a Solenoid
1. What is a solenoid and how does it produce a magnetic field?
A solenoid is a long coil of wire, often wound in the shape of a helix, which generates a uniform magnetic field when an electric current passes through it.
- It consists of closely spaced turns of insulated wire.
- The magnetic field inside a solenoid is strong and nearly uniform.
- The direction of the field depends on the direction of current, following the right-hand rule.
2. How do you calculate the magnetic field inside a solenoid?
The magnetic field (B) inside a long, ideal solenoid is calculated using the formula:
- B = μ₀ n I
- μ₀ = permeability of free space
- n = number of turns per unit length
- I = current through the coil
3. Why is the magnetic field inside a solenoid uniform and strong?
The magnetic field inside a solenoid is uniform and strong due to the close winding and alignment of wire loops.
- Current in each loop adds up, resulting in a consistent field direction.
- The central area has parallel field lines, minimizing edge effects.
- This principle is used in electromagnets and laboratory setups for constant magnetic fields.
4. What are the main applications of solenoids and their magnetic fields?
Solenoids and their magnetic fields have wide applications in science and technology.
- Electromagnets for lifting heavy objects
- Electric relays and switches
- Medical devices such as MRI machines
- Research and measurement instruments
- Door locks and automotive starters
5. How does the direction of current affect the polarity of a solenoid's magnetic field?
The direction of current through a solenoid determines the polarity (north and south pole) using the right-hand rule:
- If fingers curl in current direction, the thumb points to the north pole of the solenoid.
- Switching current direction reverses the poles.
6. What factors affect the strength of a solenoid's magnetic field?
The strength of the magnetic field inside a solenoid depends on several main factors:
- Number of turns per unit length (n): More turns make the field stronger.
- Current (I): Higher electric current increases field strength.
- Core material: Using a soft iron core amplifies the field.
7. What is the difference between a solenoid and a bar magnet?
A solenoid and a bar magnet both create similar magnetic fields but have distinct origins.
- Solenoid: Magnetic field produced by electric current in coils, can be switched on and off.
- Bar magnet: Permanent magnet, magnetic field is always present due to material properties.
- Both have north and south poles and similar field line patterns.
8. Can the magnetic field outside a solenoid be ignored? Why?
Yes, the magnetic field outside a long solenoid is very weak compared to the inside.
- Field lines are concentrated within the coil, becoming nearly parallel and dense.
- Outside, field lines spread out and cancel each other, making the external field negligible.
9. What happens if a soft iron core is inserted inside a solenoid?
Inserting a soft iron core inside a solenoid drastically increases the magnetic field strength.
- Iron core enhances magnetic permeability.
- Field lines become more concentrated.
- This combination is used for creating powerful electromagnets.
10. Why is the solenoid commonly used to demonstrate a uniform magnetic field?
A solenoid is chosen to represent a uniform magnetic field because:
- The field inside is strong and nearly constant throughout the length, especially at the center.
- It is easy to control the field by changing current or coil parameters.
- It mimics Earth’s magnetic field in laboratory conditions.
























