




How to Convert a Complex Number Between Cartesian, Polar, and Euler Forms
A complex number admits representation in rectangular, polar, and exponential (Euler) forms. Each expresses the same quantity using distinct variables, supporting different operations and geometric interpretations.
Algebraic Definition and Notation for Polar Form of a Complex Number
Definition: The rectangular form of a complex number is $z = x + iy$, where $x$ is the real part and $y$ is the imaginary part. In polar form, $z$ is expressed using its modulus $r$ and argument $\theta$ as $z = r (\cos \theta + i \sin \theta)$.
The modulus $r$ equals $\sqrt{x^2 + y^2}$, and the argument $\theta$ is determined by $\theta = \tan^{-1} \left( \dfrac{y}{x} \right)$, with quadrant adjustments as required.
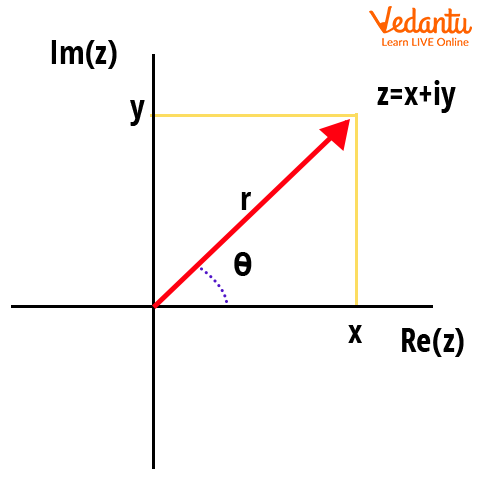
The Argand diagram illustrates the geometric interpretation, where $r$ is the distance from the origin and $\theta$ is the angle made with the positive real axis. For further reading, see Understanding Complex Numbers.
Calculation of Modulus and Argument in All Quadrants
If $z$ lies in the first or fourth quadrant, set $\theta = \tan^{-1} \left( \dfrac{y}{x} \right)$. In the second or third quadrant, use $\theta = \tan^{-1} \left( \dfrac{y}{x} \right) + \pi$ if $x < 0$.

Numerical calculations must be quadrant-aware to ensure the correct principal value for the argument. Reference: Modulus And Conjugate Of A Complex Number
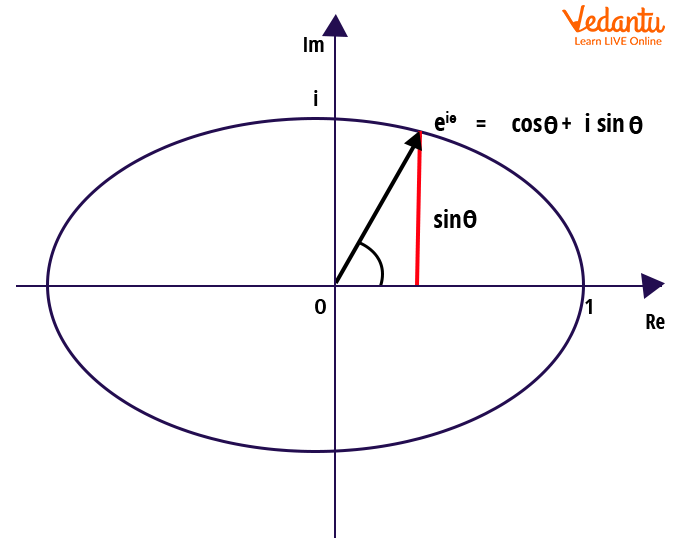
Exponential (Euler) Form and Euler’s Identity
Result: Euler’s formula establishes $e^{i\theta} = \cos\theta + i\sin\theta$ for real $\theta$. The polar form $z = r (\cos \theta + i \sin \theta)$ is thus equivalent to the exponential form $z = r e^{i\theta}$.
This form is especially useful for multiplication, division, and finding powers or roots of complex numbers, due to properties of exponents.
Power Series Justification of Euler’s Formula
Start from the real function power series: $e^{ix} = \sum_{n=0}^{\infty} \dfrac{(ix)^n}{n!}$. Expanding, group even and odd powers to obtain $e^{ix} = \cos x + i\sin x$ by comparing with the respective Maclaurin series.
Each component is justified by matching terms: real parts correspond to cosine series, imaginary parts to sine series. This underpins the equivalence of the polar and Euler forms.
Transformations: Cartesian, Polar, and Exponential Representations
To convert $z = x + iy$ to polar or Euler form, compute $r = \sqrt{x^2 + y^2}$ and $\theta = \tan^{-1}(y/x)$. Then $z = r (\cos \theta + i\sin \theta) = r e^{i\theta}$.
Conversely, to express $z = r e^{i\theta}$ in rectangular form, use $x = r \cos \theta$, $y = r \sin \theta$ for $z = x + iy$. For related transformations, see Polar And Eular Form.
Illustrative Calculations Using Euler and Polar Forms
Example: Evaluate $e^{i\pi/6}$.
Substitute $x = \pi/6$ in Euler’s identity: $e^{i\pi/6} = \cos(\pi/6) + i\sin(\pi/6)$.
$\cos(\pi/6) = \dfrac{\sqrt{3}}{2}$, $\sin(\pi/6) = \dfrac{1}{2}$.
Final result: $e^{i\pi/6} = \dfrac{\sqrt{3}}{2} + i \dfrac{1}{2}$.
Example: Convert $z = -3 + 3\sqrt{3}i$ to exponential form.
$r = \sqrt{(-3)^2 + (3\sqrt{3})^2} = \sqrt{9 + 27} = \sqrt{36} = 6$.
$\theta = \tan^{-1} \left(\dfrac{3\sqrt{3}}{-3}\right) = \tan^{-1}(-\sqrt{3})$. Since $x < 0$, add $\pi$ for a second-quadrant angle: $\theta = \frac{2\pi}{3}$.
Final result: $z = 6 e^{i\frac{2\pi}{3}}$.
Example: Find the product of $z_1 = 4 e^{i\frac{\pi}{4}}$ and $z_2 = 3 e^{i\frac{\pi}{6}}$.
Multiply moduli and add arguments: $z_1 z_2 = (4 \times 3) e^{i(\frac{\pi}{4} + \frac{\pi}{6})} = 12 e^{i\frac{5\pi}{12}}$.
For advanced usage, such as geometrical rotations and scaling, refer to Concept Of Rotation in Complex Numbers.
Notational Distinctions and Misconceptions in Polar and Exponential Forms
Common Error: Using incorrect argument branch in quadrant determination results in a wrong representation.
Carefully distinguish between argument range $(-\pi, \pi]$ and $[0, 2\pi)$ according to problem requirements. Maintain principal value consistency throughout calculations.
Typical JEE Patterns: Operations in Polar and Euler Forms
- Multiplication: moduli multiply, arguments add
- Division: moduli divide, arguments subtract
- Powers: moduli raised to power, arguments multiplied
- Roots: moduli rooted, multiple arguments spaced evenly
Mastering these rules streamlines solutions and avoids algebraic errors in exam applications
FAQs on Understanding the Polar and Euler Forms of Complex Numbers
1. What is the polar form of a complex number?
The polar form of a complex number expresses it using its magnitude and argument (angle) instead of its real and imaginary parts. In the polar form, a complex number z = x + iy is represented as:
- z = r (cos θ + i sin θ), where
- r = |z| = √(x² + y²) is the modulus (magnitude), and
- θ = arg(z) = tan-1(y/x) is the argument (angle).
2. What is Euler's form of a complex number?
Euler's form expresses a complex number using the exponential function with an imaginary exponent. According to Euler's formula:
- z = reiθ, where
- r is the modulus of the complex number, and
- θ is the argument (angle in radians).
3. How do you convert a complex number from Cartesian to polar form?
To convert a complex number from Cartesian (rectangular) to polar form, calculate its modulus and argument.
- Given z = x + iy:
- Modulus (r) = √(x² + y²)
- Argument (θ) = tan-1(y/x)
- Express as z = r (cos θ + i sin θ)
4. Why is polar form useful in complex number multiplication and division?
The polar form simplifies multiplication and division of complex numbers by handling magnitudes and angles separately.
- For multiplication: Multiply the moduli and add the arguments.
- For division: Divide the moduli and subtract the arguments.
- Example: If z₁ = r₁ cis θ₁ and z₂ = r₂ cis θ₂, then z₁z₂ = r₁r₂ cis(θ₁ + θ₂).
5. State Euler’s formula and explain its significance.
Euler’s formula establishes the deep link between exponential and trigonometric functions for complex numbers.
- eiθ = cos θ + i sin θ
- It allows any complex number to be written as z = reiθ
- Widely used in signal processing, physics, electrical engineering, and mathematics
6. How can you write a complex number in exponential form?
A complex number can be written in exponential form using Euler’s formula with modulus and argument.
- Given z = x + iy, calculate r = √(x² + y²) and θ = tan-1(y/x)
- Express as z = reiθ
7. What are the main advantages of representing complex numbers in polar or Euler form?
Representing complex numbers in polar or Euler form offers several advantages:
- Makes multiplication, division, powers, and roots simpler
- Gives a clear geometric interpretation
- Facilitates use in electrical engineering, signal processing, and mathematics
- Simplifies working with oscillations and waveforms
8. What is the modulus and argument of a complex number?
The modulus and argument are polar coordinates describing a complex number’s distance and angle from the origin.
- Modulus (r): The length from the origin, r = √(x² + y²)
- Argument (θ): The angle with the positive x-axis, θ = tan-1(y/x)
9. Define the principal value of the argument of a complex number.
The principal value of the argument is the unique angle θ that lies within the interval (–π, π].
- Calculated using tan-1(y/x) and adjusted to fit within (–π, π]
- Ensures each complex number has only one principal argument
10. If z = 1 – i, write it in polar and Euler form.
To write z = 1 – i in polar and Euler form, find its modulus and argument first:
- r = √(1² + (–1)²) = √2
- θ = tan-1(–1/1) = –π/4 (or –45°)
- Polar form: √2 (cos(–π/4) + i sin(–π/4))
- Euler form: √2 e–iπ/4
























