Maxwells Distribution of Velocities: Understanding Molecular Speed and Kinetic Theory
Maxwell's Distribution of Velocities is a key concept in kinetic theory and thermodynamics, explaining the distribution of molecular speeds in a gas at a given temperature. Proposed by James Clerk Maxwell and expanded by Ludwig Boltzmann, this distribution helps students understand how molecular motion varies due to collisions and temperature changes. For JEE Main 2025, this topic is crucial for mastering gas laws, energy calculations, and the behaviour of ideal gases. By learning this, students can tackle questions on molecular speeds, temperature effects, and the relationship between the most probable, average, and root mean square speeds effectively.
What is Maxwells Distribution of Molecular Velocities
The Maxwell-Boltzmann distribution (also known as the Maxwell distribution) is a statistical representation of the energy of molecules in a classical gas. The distribution of velocities among the molecules of gas was initially proposed by Scottish physicist James Clerk Maxwell in 1859, based on probabilistic reasons. German scientist Ludwig Boltzmann expanded Maxwell's result in 1871 to express the distribution of energy among molecules.
The Maxwell-Boltzmann Distribution of Velocity
Gas is made up of thousands of microscopic particles (atoms or molecules) separated by enormous empty gaps. These particles move in all directions all of the time. They collide with each other as well as the container's walls while in motion. The molecules' speed and directions are constantly changing as a result of these collisions. As a result, the speed of all the molecules in a particular gas sample is not the same. Individual molecule speeds vary and are distributed over a broad range. Even if all of the particles started at the same speed, molecular collisions will cause them to move at different speeds. The speeds of various molecules are also changing. However, at a given temperature, the distribution of speeds among different molecules remains constant, despite changes in individual speeds.
As a result, the fraction of molecules with a specific speed remains constant. As they were the first to formulate it, it is known as the distribution of speeds as well as the Maxwell-Boltzmann distribution law or Maxwell law. Maxwell and Boltzmann plotted the fraction of molecules that move at different speeds (along the y-axis), against the speeds of the molecules (along the x-axis). The resulting curve is known as ‘Maxwell's distribution curve’.
Maxwell Distribution of Velocities
The following are the key characteristics of the Maxwell distribution of velocities:
(i) The fraction of molecules with extremely low or extremely high velocities is extremely small.
(ii) The fraction of molecules with higher velocities increases until it reaches a plateau, at which point it begins to decline.
(iii) The maximum fraction of molecules has a velocity, which corresponds to the curve's peak. This is referred to as the most likely velocity.
Thus, the most likely speed of a gas is the speed of the greatest fraction of gas molecules at a given temperature.
The Effect of Temperature on Speed Distribution
The increase in molecular motion occurs as the temperature of the gas rises. As the temperature rises, so does the value of the most likely speed (up). In fact, as the temperature rises, the entire distribution curve shifts to the right. In other words, as temperatures rise, the curve broadens. It should be noted, however, that if the temperature remains constant, the distribution of speeds among molecules does not change.
The speed distribution at a given temperature is also affected by the mass of the molecules. At the same temperature, heavier gas molecules move slower than lighter gas molecules. Lighter nitrogen molecules, for example, move faster than heavier chlorine molecules. As a result, at any given temperature, nitrogen molecules are more likely to move than chlorine molecules. Image 2 shows the molecular speed distribution curves for chlorine and nitrogen.
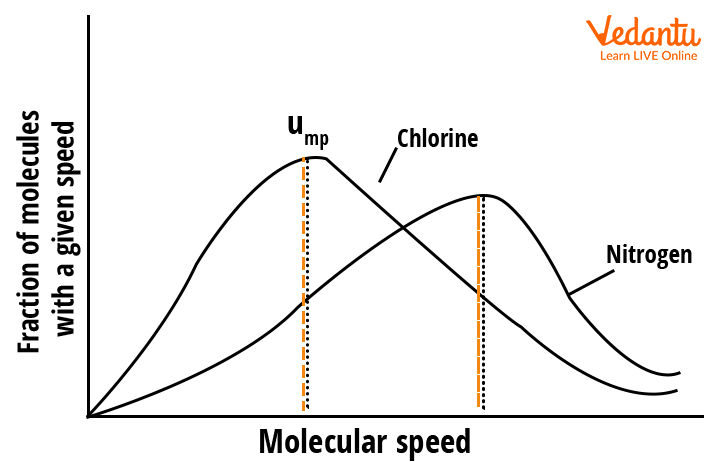
The Molecular Speed Distribution Curves for Chlorine and Nitrogen.
Maxwell Distribution of Molecular Velocities Derivation
The Most Probable Speed
The most probable speed of a gas's molecules is the speed possessed by the greatest fraction of the total number of molecules in the gas.
For example, if the speeds of ten molecules of a gas are 1, 2, 2, 3, 3, 3, 4, 5, 6, 6, km/s, the most likely speed is 3 km/s, because the maximum fraction of total molecules poses this speed, i.e. most probable speed , $C_{mp}=3~\dfrac{km}{s}$ . It should be noted that the subscript maximum refers to the maximum fraction of molecules, not the maximum speed.
It can be shown that,
$C_{m p}=\sqrt{\dfrac{2 k_{B} T}{m}}$
Where m is the molecule's mass, kB is the Boltzmann constant and T is the gas's temperature. For a given gas, the value of most likely speed vmax decreases as temperature rises.
Mean Speed or Average Speed (Cav)
Average speed is the average speed of a gas molecule. It equals the sum of the individual molecule speeds divided by the number of molecules. If C1+C2+C3+......Cn are the individual molecule speeds, their mean or average speed is
$C_{a v}=\dfrac{C_{1}+C_{2}+\ldots+C_{n}}{n}$
Using Maxwellian speed distribution law, we can show that,
$C_{a v}=\sqrt{\dfrac{8 k_{B} T}{m \pi}}$
Where m is the mass of each molecule,
kB is the Boltzmann constant and T is the temperature.
Root Mean Square Speed Cmax
The square root of the mean of the squares of the random velocities of individual gas molecules is defined as the root mean square speed of gas molecules. If C1,C2,...,Cn are random velocities of n molecules of a gas, then the RMS speed of molecules is:
$C_{r m s}=\sqrt{\dfrac{C_{1}^{2}+C_{2}^{2}+\ldots C_{n}^{2}}{n}}$
We can deduce from the Maxwellian speed distribution law that
$C_{r m s}=\sqrt{\dfrac{{ }^{3 k_{B} T}}{m}}$
where the symbols have their usual meaning.
Relationship between different types of Speeds
The root mean square speed $(\bar{u_{rms}})$, most probable speed, ump and average speed, uav are given by the expressions:
The root mean square speed is a common measurement that can be calculated using the following relationships:
$u_{r m s}=\sqrt{\dfrac{3 R T}{M}} \text { or } \sqrt{\dfrac{3 p V}{M}} \text { or } \sqrt{\dfrac{3 p}{\rho}}$
Application of Distribution Law
The Maxwell-Boltzmann equation, which serves as the foundation of gas kinetic theory, defines the distribution of speeds for gas at a given temperature. This distribution function can calculate the most likely speed, average speed, and root-mean-square speed.
The Maxwell–Boltzmann distribution is a probability distribution used in physics and chemistry. The field of statistical mechanics is the most common application. The temperature of any (massive) physical system is determined by the motions of its molecules and atoms.
Applications of Maxwell-Boltzmann Distribution
It explains how molecular speeds are distributed in a gas at a given temperature, providing insights into gas behaviour under different conditions.
Maxwell-Boltzmann distribution forms the basis of the kinetic theory of gases, which helps in understanding pressure, temperature, and energy relationships in gases.
The distribution is crucial for determining the fraction of molecules with sufficient energy to overcome the activation energy barrier in chemical reactions.
It aids in calculating properties like diffusion, viscosity, and thermal conductivity by analysing the motion of gas molecules.
In astrophysics, it is used to study the velocities of particles in stars and interstellar gases, providing insights into cosmic phenomena.
Maxwells Law Of Distribution Of Velocities shows how molecular speeds increase with temperature, helping in understanding processes like evaporation and gas expansion.
Conclusion
From the above discussion, we understand the Maxwell distribution and distribution of velocities of various molecules and distribution of molecular velocities derivation and different types of speed. There are some characteristics of Maxwell distribution, like the most likely velocity is the velocity that the maximum fraction of molecules has, which corresponds to the curve's peak. We also learned the effect of temperature and that the distribution of velocities stays constant if the temperature is unchanged. An increase in temperature increased the molecular speed, hence shifting the curve towards the right.
JEE Main 2025 Subject-Wise Important Chapters
The JEE Main 2025 subject-wise important chapters provide a focused strategy for Chemistry, Physics, and Maths. These chapters help students prioritise their preparation, ensuring they cover high-weightage topics for better performance in the exam.
Check Other Important Links for JEE Main 2025
JEE 2025 needs well-structured study materials. Here are some valuable resources to help you plan your preparation and practice efficiently.
FAQs on JEE Main 2025 Physics Maxwells Distribution of Velocities
1. What are the four assumptions of gas kinetic theory and which of the following matter states has the greatest kinetic energy?
The kinetic-molecular theory of gases assumes that ideal gas molecules (1) are constantly moving, (2) have negligible volume, (3) have negligible intermolecular forces, and (4) collide perfectly elastically. When heat is supplied, the temperature of a substance rises in proportion to an increase in either the average kinetic energy of the particles, the average potential energy of separation (as in fusion) or both.
A pure substance in the gaseous state has more energy than a pure substance in the liquid state, which in turn has more energy than a pure substance in the solid-state. When particles are gaseous, they have the greatest kinetic energy.
2. In Maxwell's equations, what two fundamental forces are described, and what influences gas molecules' molecular velocity?
In the Maxwell equation, two fundamental forces are explained. These are fundamental laws of electricity and magnetism. Maxwell Distribution equations describe how electric and magnetic fields interact with one another as well as charges and currents.
The speed of molecules in a gas is related to temperature but inversely proportional to the gas's molar mass. In other words, as the temperature of a gas sample rises, the molecules speed up, increasing the root mean square molecular speed. if the temperature remains constant, then the distribution of speeds among molecules also remains constant.
3. What is the distinction between an average and an RMS value?
The most probable speed is the one that indicates the maximum number of molecules in the gas. The maximum value on Maxwell's distribution plot represents the most likely speed. The average speed is calculated by adding the speeds of all molecules and dividing the total number of molecules by the number of molecules. The square root of the average velocity squared of the molecules in a gas is used to calculate the speed of particles in a gas. This is the root mean square speed.
4. What is Maxwell's Distribution of Velocities?
Maxwell's Distribution of Velocities describes the statistical distribution of speeds among molecules in a gas. It explains that not all molecules move at the same speed, but their speeds are distributed over a range at a given temperature.
5. How does Maxwell's Distribution of Molecular Velocities depend on temperature?
As temperature increases, the distribution curve shifts to the right, indicating that the molecules have higher speeds. The most probable speed, average speed, and root mean square speed all increase with temperature.
6. What is the significance of Maxwell's Law of Distribution of Velocities?
Maxwell's law explains how molecular speeds in a gas are distributed, helping predict the behaviour of gases under different conditions, such as diffusion, effusion, and energy transfer.
7. How is the most probable speed derived from Maxwell's Distribution of Molecular Velocities?
The most probable speed is derived from the Maxwell-Boltzmann distribution formula and is given by:
$C_{mp} = \sqrt{\frac{2k_B T}{m}}$
where$k_B$ is the Boltzmann constant, T is temperature, and mmm is the molecule's mass.
8. What is the difference between Maxwell's Distribution of Velocities and Molecular Velocities?
Maxwell's Distribution of Velocities refers to the statistical representation of speeds in a gas, while molecular velocities focus on the actual individual speeds of molecules within that distribution.
9. How does molar mass affect Maxwell's Distribution of Velocities?
Heavier molecules (higher molar mass) move slower than lighter molecules at the same temperature, resulting in a narrower and steeper distribution curve for heavier gases.
10. Why is Maxwell's Law of Distribution of Velocities important in thermodynamics?
It provides a foundation for understanding gas behaviour, energy distribution, and properties like pressure, temperature, and heat capacity in thermodynamics.
