




How Does Centripetal Force Work in Real Life?
Centripetal force is a fundamental concept in classical mechanics that describes the force required to keep an object moving in a circular path. It always acts towards the centre of the circle and is perpendicular to the object's instantaneous displacement. Understanding centripetal force is essential for solving problems involving circular motion in physics, especially in examinations like JEE Main.
Centripetal Force: Definition and Meaning
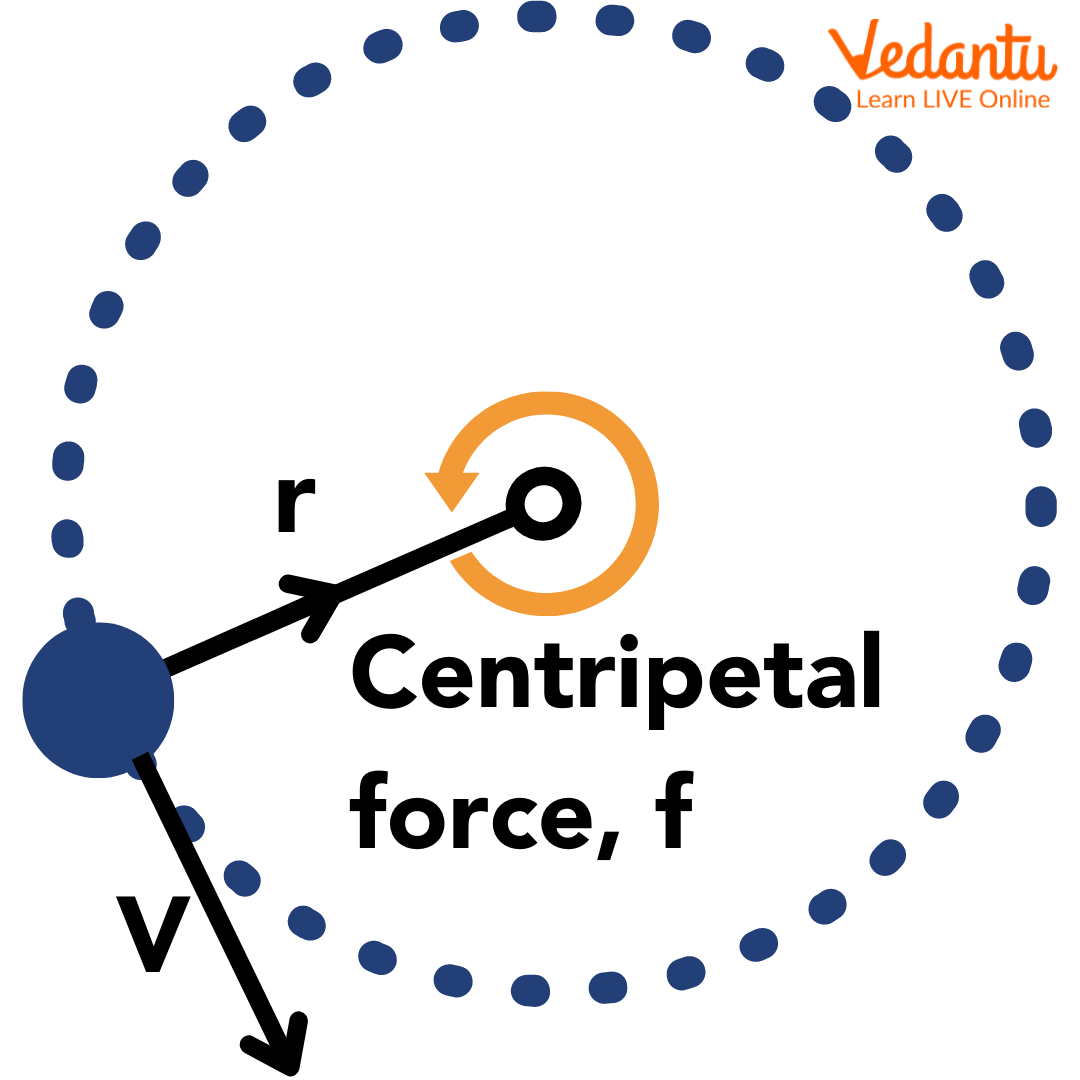
Centripetal force is defined as the net force acting on an object that moves along a circular path, directed toward the centre of the circle. This force ensures that the object remains in its curved trajectory and does not move in a straight line due to inertia.
The direction of the centripetal force is always towards the centre of the circular path, making it perpendicular to the velocity of the object at every point on the trajectory.
Centripetal Force Formula
For an object of mass $m$ moving with velocity $v$ in a circle of radius $r$, the centripetal force $F$ is given by the equation:
$F = \dfrac{mv^{2}}{r}$
This relation shows that the required centripetal force increases with the object's mass and the square of its velocity but decreases with the radius of the circle. The SI unit of centripetal force is Newton (N).
Dimensional Formula of Centripetal Force
The dimensional formula helps verify the correctness of the equation and analyze the physical quantity in terms of fundamental dimensions. For centripetal force, the dimensional analysis is as follows:
| Physical Quantity | Dimensional Formula |
|---|---|
| Mass (m) | M |
| Velocity (v) | LT^{-1} |
| Radius (r) | L |
| Centripetal Force (F) | MLT^{-2} |
The dimensional formula for centripetal force, $MLT^{-2}$, is identical to that of any force, confirming the equation's consistency. For more insight on related force concepts, refer to Force on a Current-Carrying Conductor.
Characteristics of Centripetal Force
Centripetal force has distinct characteristics that are important in the study of circular motion. It is not a unique type of force but is provided by different real forces depending on the situation, such as gravitational, frictional, or tension forces.
- Always directed towards the circle's centre
- Responsible for changing the direction of velocity
- Magnitude is proportional to mass and velocity squared
- Inversely proportional to radius
The physical nature of the centripetal force depends on the system, and it does not depend on the direction of rotation of the object.
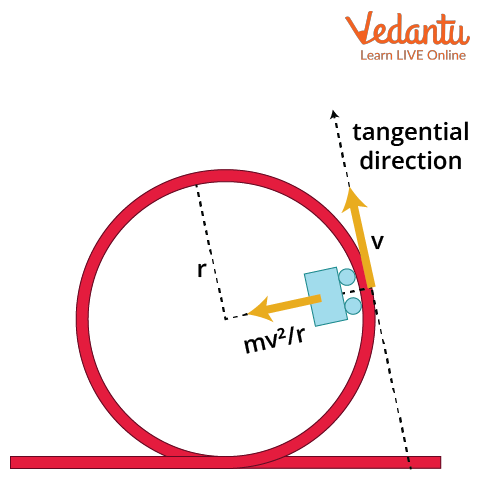
Work Done by Centripetal Force
Work done is given by the product of the force and displacement in the direction of the force. In circular motion, the centripetal force and the instantaneous displacement of the object are perpendicular to each other.
Since the angle between the force and displacement at every instant is $90^\circ$, the work done by the centripetal force over any displacement is zero: $W = F \cdot S \cos 90^\circ = 0$.
Centripetal Acceleration
Centripetal acceleration is the acceleration experienced by an object moving in a circular path, always directed toward the centre. It is given by:
$a = \dfrac{v^2}{r}$
Even for constant speed, this acceleration is present due to the continuous change in direction of velocity. To understand more about acceleration concepts, refer to Acceleration Due to Gravity.
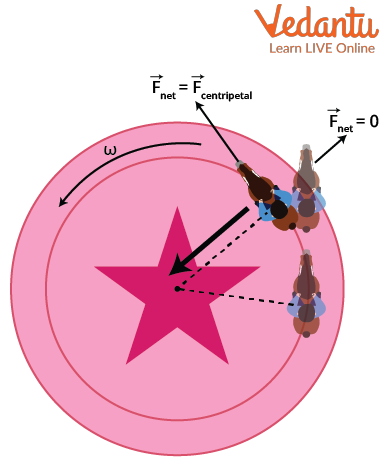
Examples of Centripetal Force in Daily Life
Centripetal force is observed in various systems and devices designed to maintain circular motion. The actual force providing the necessary centripetal force can be tension, gravity, friction, or the normal reaction.
- Roller coaster: normal force from the track provides centripetal force
- Merry-go-round: frictional force acts as the centripetal force
- Centrifuge machine: tension and reaction forces maintain circular path
- Washing machine dryer: clothes experience normal contact force


In planetary motion, the gravitational pull acts as the centripetal force, keeping planets in their orbits. For more details about the comparison of forces in circular motion, see Understanding Circular Motion.
Solved Example on Centripetal Acceleration
A ball attached to a string of length $1.5\,\mathrm{m}$ completes two full rotations every second. The frequency $f = 2\,\mathrm{Hz}$, so the circumference $C = 2\pi r = 3\pi\,\mathrm{m}$. The velocity $v = C \cdot f = 6\pi\,\mathrm{m/s}$.
Centripetal acceleration $a$ is calculated as:
$a = \dfrac{v^2}{r} = \dfrac{(6\pi)^2}{1.5} = \dfrac{36\pi^2}{1.5} = 24\pi^2\,\mathrm{m/s^2}$
This example demonstrates the application of centripetal force concepts to a circular motion problem.
Factors Affecting Centripetal Force
Several parameters impact the magnitude of the required centripetal force for a given circular motion. The factors involved are:
- Greater mass increases required force
- Higher velocity greatly raises the force (depends on $v^2$)
- Larger radius reduces required force
These relationships are indicated in the centripetal force equation. To expand on the differences between work, energy, and power in such contexts, review Difference Between Work and Energy.
Distinction: Centripetal Force vs. Centrifugal Force
Centripetal force is the actual force required to maintain circular motion, acting towards the centre. In contrast, centrifugal force appears as a pseudo-force perceived by an observer in a rotating reference frame, directed away from the centre.
For an in-depth distinction, refer to Centrifugal Force Explained.
Summary of Centripetal Force Concepts
Centripetal force is essential for understanding motion in a circle. It always acts toward the centre and depends on mass, velocity, and radius. The force may arise due to tension, gravity, friction, or normal contact depending on the context.
Mastery of centripetal force and related circular motion topics is necessary for clear understanding in mechanics and JEE-level problem solving. For a broader view of energy considerations, see Work, Energy and Power Overview.
FAQs on Understanding Centripetal Force in Physics
1. What is centripetal force?
Centripetal force is the required force that keeps an object moving in a circular path by constantly pulling it towards the center of the circle.
Key points:
- Centripetal force acts perpendicular to the object's velocity and towards the center.
- It does not do work as it does not change the object's speed, only its direction.
- Examples include tension in a string, friction on a car’s tires, or gravitational pull in planetary orbits.
2. What provides the centripetal force in different circular motions?
The source of centripetal force depends on the context of the circular motion.
- Tension in a string for a swinging object.
- Friction between car tires and the road for vehicles turning.
- Gravitational force for planets in orbit.
- Normal reaction for a vehicle going over a hill.
3. What is the mathematical formula for centripetal force?
The formula for centripetal force is:
F = (mv²) / r
- F = Centripetal force
- m = Mass of the object (kg)
- v = Speed of the object (m/s)
- r = Radius of the circular path (m)
4. What is the difference between centripetal and centrifugal force?
Centripetal force is a real force directed towards the center of a circle, keeping an object in circular motion, whereas centrifugal force is a fictitious force perceived in a rotating frame, appearing to act outward.
Differences:
- Centripetal force is experienced in an inertial (real) frame; centrifugal force arises in a non-inertial (rotating) frame.
- Centripetal is required for actual motion, centrifugal is apparent to the rotating observer.
5. How does centripetal force affect motion on a banked road?
On a banked road, the normal reaction and friction together provide the required centripetal force, so vehicles can turn safely without skidding.
- Banking reduces reliance on friction alone.
- At the correct banking angle, cars can make turns even on slippery surfaces.
- Formula for banking angle: tanθ = v²/rg.
6. What are some real-life examples of centripetal force?
Real-life examples of centripetal force include:
- Planets revolving around the Sun due to gravitational pull.
- A car taking a circular turn, where friction acts as the centripetal force.
- A stone tied to a string and whirled in a circle (tension provides centripetal force).
- Cyclists turning on curved tracks.
7. Why is centripetal force called a necessary force for circular motion?
Centripetal force is necessary because, without it, an object would move in a straight line due to inertia (Newton's first law).
- It ensures the object changes direction continuously, maintaining circular motion.
- No centripetal force = no circular path.
8. How do you calculate the centripetal force acting on a car moving in a circle of radius r at speed v?
To calculate centripetal force on a car in a circle:
- Use the formula: F = (mv²) / r
- Where m = mass of the car, v = speed, and r = radius of circle.
9. What happens if the required centripetal force is not available?
If the required centripetal force is absent, the object will move off in a straight line tangential to the circular path due to inertia.
- Vehicles may skid outward when turning at high speed.
- Planets would leave their orbits if the force vanished.
10. Is centripetal force a type of new force?
Centripetal force is not a new or separate force but is the name given to whatever physical force provides the required inward acceleration in circular motion.
- It can be tension, friction, gravity, or normal reaction, depending on the situation.
11. What is the direction of centripetal force at any point on the circular path?
At every instant, the centripetal force acts perpendicular to the velocity of the object and is always directed towards the center of the circular path.
12. Name some forces that can act as centripetal force during different types of circular motion.
Some forces that can act as centripetal force are:
- Gravitational force (e.g., satellite orbiting Earth)
- Tension force (e.g., swinging a ball attached to a string)
- Frictional force (e.g., bicycle taking a turn)
- Electrostatic force (in electrons revolving around the nucleus)


































