Important Questions for CBSE Class 10 Maths Chapter 12 - Surface Areas and Volumes 2024-25

Problems Based on Conversion of Solids

1. A solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is $3.5$ cm and the height of the cone is $4$ cm. The solid is placed in a cylindrical tub, full of water, in such a way that the whole solid is submerged in water. If the radius of the cylindrical tub is $5$ cm and its height is $10.5$ cm, find the volume of water left in the cylindrical tub. Use $\pi =\dfrac{22}{7}$. 

Ans: Given, the radius of the cylinder is $5cm$ and its height is $10.5cm$.

Volume of cylinder is $\pi {{\left( 5 \right)}^{2}}\times 10.5=262.5\pi $ 

Given, radius of hemisphere is $3.5cm$.

Volume of hemisphere is $\dfrac{2}{3}\pi {{\left( 3.5 \right)}^{3}}=28.6\pi $ 

Volume of cone is $\dfrac{1}{3}\pi {{\left( 3.5 \right)}^{2}}4=16.34\pi $ 

Volume of water left in the cylinder is

$\Rightarrow 262.5\pi -28.6\pi -16.34\pi $ 

$\Rightarrow 217.56\pi $

$\Rightarrow 217.56\times \dfrac{22}{7}c{{m}^{3}}$

$\Rightarrow 683.8c{{m}^{3}}$

Therefore, the volume of water to left in a cylindrical tub is $683.8c{{m}^{3}}$.

2. A bucket of height $8$ cm and made up of copper sheet is in the form of a frustum of a right circular cone with radii of its lower and upper ends as $3$ cm and $9$ cm respectively. Calculate

(i). The height of the cone of which the bucket is a part

Ans: Given the radii of the lower and upper ends of a frustum cone are $3$ cm and $9$ cm.

${{r}_{1}}=9cm$ and ${{r}_{2}}=3cm$ 

Height $=8cm$

Let ${{h}_{1}}$ be the height of the cone of which the bucket is the part.

We get

$\Rightarrow {{h}_{1}}=\dfrac{h{{r}_{1}}}{{{r}_{1}}-{{r}_{2}}}$ 

$\Rightarrow {{h}_{1}}=\dfrac{8\times 9}{9-3}$

$\Rightarrow {{h}_{1}}=\dfrac{72}{6}$

$\therefore {{h}_{1}}=12cm$

(ii). The volume of water which can be filled in the bucket

Ans: Given the radii of the lower and upper ends of a frustum cone are $3$ cm and $9$ cm.

${{r}_{1}}=9cm$ and ${{r}_{2}}=3cm$ 

Height $=8cm$ 

Now, volume of water which can be filled in the bucket is 

\[\Rightarrow \dfrac{1}{3}\pi h\left[ r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right]\] 

\[\Rightarrow \dfrac{1}{3}\pi \times 8\left[ {{9}^{2}}+{{3}^{2}}+9\times 3 \right]\]

\[\Rightarrow \dfrac{1}{3}\pi \times 8\left[ 81+9+27 \right]\]

\[\Rightarrow \dfrac{1}{3}\pi \times 8\times 117\]

\[\Rightarrow 312\pi \text{ }c{{m}^{3}}\] 

Therefore, volume of water which can be filled in the bucket is \[312\pi \text{ }c{{m}^{3}}\]. 

(iii). The area of the copper sheet required to make the bucket (Leave the answer in terms of $\pi $. 

Ans: Given the radii of the lower and upper ends of a frustum cone are $3$ cm and $9$ cm.

${{r}_{1}}=9cm$ and ${{r}_{2}}=3cm$ 

Height $=8cm$ 

Area of copper sheet required to make the bucket is equal to the surface area of bucket.

Surface area of bucket $=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l+\pi r_{2}^{2}$ 

$\Rightarrow \text{Surface area}=\pi \left( {{r}_{1}}+{{r}_{2}} \right)\sqrt{{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}+{{h}^{2}}}+\pi r_{2}^{2}$

$\Rightarrow \text{Surface area}=\pi \left( 9+3 \right)\sqrt{{{\left( 9-3 \right)}^{2}}+{{8}^{2}}}+\pi {{\left( 3 \right)}^{2}}$

\[\Rightarrow \text{Surface area}=\pi \times 12\sqrt{36+64}+\pi \times 9\]

\[\Rightarrow \text{Surface area}=120\pi +9\pi \]

$\therefore \text{Surface area}=129\pi \text{ }c{{m}^{2}}$

3. A sphere and a cube have equal surface areas. Show that the ratio of the volume of the sphere to that of the cube is $\sqrt{6}:\sqrt{\pi }$.

Ans: Given that a sphere and cube have equal surface areas.

We get

$\Rightarrow 4\pi {{r}^{2}}=6{{a}^{2}}$

$\Rightarrow r=\sqrt{\dfrac{6{{a}^{2}}}{4\pi }}$ 

Now, ratio of the volumes is

$\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{\dfrac{4}{3}\pi {{r}^{3}}}{{{a}^{3}}}$ 

$\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{\dfrac{4}{3}\pi {{\left( \sqrt{\dfrac{6{{a}^{2}}}{4\pi }} \right)}^{3}}}{{{a}^{3}}}$

$\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{\dfrac{4}{3}\pi \times {{a}^{3}}{{\left( \sqrt{\dfrac{6}{4\pi }} \right)}^{3}}}{{{a}^{3}}}$

$\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{4}{3}\pi {{\left( \sqrt{\dfrac{6}{4\pi }} \right)}^{3}}$

\[\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{4}{3\times {{2}^{3}}}\pi {{\left( \sqrt{\dfrac{6}{\pi }} \right)}^{3}}\]

\[\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{1}{3\times 2}\pi {{\left( \sqrt{\dfrac{6}{\pi }} \right)}^{3}}\]

\[\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{\pi }{6}{{\left( \dfrac{6}{\pi } \right)}^{\dfrac{3}{2}}}\]

\[\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\sqrt{\dfrac{6}{\pi }}\]

Therefore, the volume of the sphere to that of the cube is $\sqrt{6}:\sqrt{\pi }$.

4. A right triangle, whose sides are $15$ cm and $20$ cm is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. 

Ans: Given the sides of a triangle are $15$ cm and $20$ cm. 

Hypotenuse of triangle is $BC=\sqrt{{{15}^{2}}+{{20}^{2}}}=25cm$ 

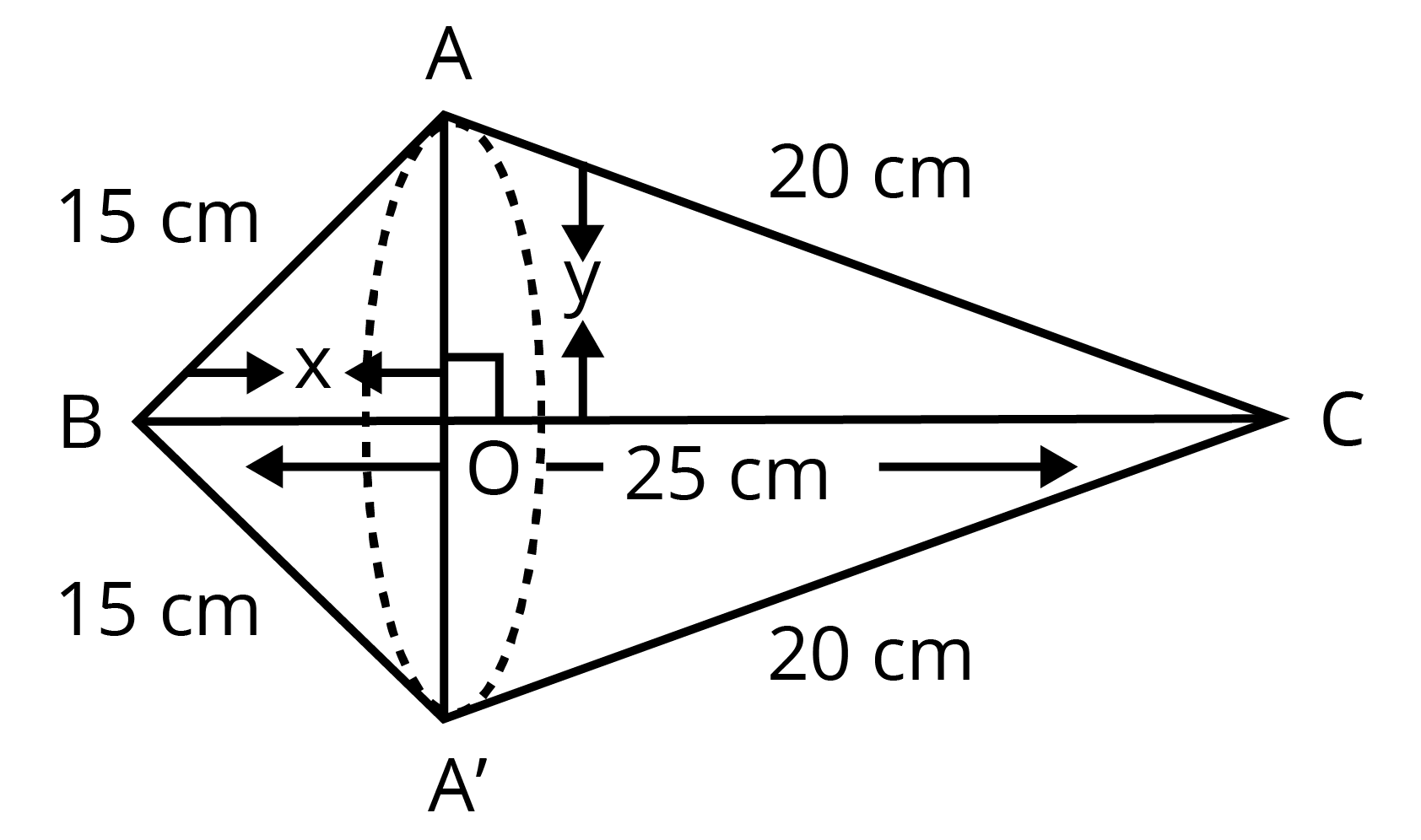
From figure,

By Pythagoras theorem, in $\Delta OAB$,

We get

${{\left( 15 \right)}^{2}}={{\left( OB \right)}^{2}}+{{\left( OA \right)}^{2}}$ 

\[\Rightarrow {{\left( OA \right)}^{2}}=225-{{\left( OB \right)}^{2}}\]…….(1)

By Pythagoras theorem, in $\Delta OAC$,

We get

${{\left( OA \right)}^{2}}=400-{{\left( 25-OB \right)}^{2}}$….(2)

From eq. (1) and (2), we get

\[\Rightarrow 225-{{\left( OB \right)}^{2}}=400-{{\left( 25-OB \right)}^{2}}\]

\[\Rightarrow 225-{{\left( OB \right)}^{2}}=400-625-{{\left( OB \right)}^{2}}+50\times OB\]

\[\Rightarrow 225=400-625+50\times OB\]

\[\Rightarrow 225+225=50\times OB\]

\[\Rightarrow OB=\dfrac{450}{50}\]

\[\therefore OB=9cm\] height of cone

 Now, from eq. (1), We get

\[\Rightarrow {{\left( OA \right)}^{2}}=225-81\]

\[\Rightarrow {{\left( OA \right)}^{2}}=144\]

\[\therefore OA=12cm\] radius of cone

Now, volume of double cone is given as

$\Rightarrow \dfrac{1}{3}\pi {{\left( 12 \right)}^{2}}\left( 16 \right)+\dfrac{1}{3}\pi {{\left( 12 \right)}^{2}}\left( 9 \right)$ 

$\Rightarrow \dfrac{1}{3}\times 3.14\times 144\times 16+\dfrac{1}{3}\times 3.14\times 144\times 9$

$\Rightarrow \dfrac{1}{3}\times 3.14\times 144\left[ 16+9 \right]$

$\Rightarrow \dfrac{1}{3}\times 3.14\times 144\times 25$

$\therefore Volume=3768c{{m}^{3}}$

Surface area of double cone is given as

$\Rightarrow \pi \times 12\times 15+\pi \times 12\times 20$

$\Rightarrow 12\pi \left( 15+20 \right)$

$\Rightarrow 3.14\times 12\times 35$

$\therefore \text{surface area}=1318.8c{{m}^{2}}$

5. Water in a canal $30dm$ wide and $12dm$ deep is flowing with a velocity of $10km/h$. How much area will it irrigate in $30$ minutes if $8cm$ of standing water is required for irrigation?

Ans: Given the width of canal is $30dm=3m$ and

Depth of canal is $12dm=1.2m$

Velocity of water is $10km/h=10000m/h$.

Length of water column formed in $30$ minutes is $10000\times \dfrac{1}{2}=5000m$ 

Let $x$ be the area to be irrigated.

We get

$\Rightarrow x\times \dfrac{8}{100}=5000\times 1.2\times 3$ 

$\Rightarrow x\times \dfrac{8}{100}=18000$

$\Rightarrow x=\dfrac{18000\times 100}{8}$

$\therefore x=225000{{m}^{2}}$

Therefore, $225000{{m}^{2}}$ area will be irrigated.

6. A cylindrical vessel of diameter $14cm$ and height $42cm$ is fixed symmetrically inside a similar vessel of diameter $16cm$ and height $42cm$. The total space between the two vessels is filled with cork dust for heat insulation purposes. How many cubic centimeters of cork dust will be required?

Ans: Given the diameter of the cylindrical vessel is $14cm$ and height $42cm$.

So the radius is $r=7cm$ 

Also given the diameter of another vessel is $16cm$ and height $42cm$. 

So the radius is $R=8cm$ 

Volume of cork dust required is 

$\Rightarrow \pi {{R}^{2}}h-\pi {{r}^{2}}h$ 

$\Rightarrow \pi h\left( {{R}^{2}}-{{r}^{2}} \right)$

$\Rightarrow 42\pi \left( {{8}^{2}}-{{7}^{2}} \right)$

$\Rightarrow 42\times \dfrac{22}{7}\left( 64-49 \right)$

$\Rightarrow 42\times \dfrac{22}{7}\times 15$

$\Rightarrow 1980c{{m}^{3}}$

Therefore, the volume of cork dust required is $1980c{{m}^{3}}$.

7. A building is in the form of a cylinder surrounded by a hemispherical vaulted dome and contains $41\dfrac{19}{21}$ cu m of air. If the internal diameter of the building is equal to its total height above the floor, find the height of the building.the 

Ans: Given the volume of building is $41\dfrac{19}{21}{{m}^{3}}$.

We get

$\Rightarrow \pi {{r}^{2}}\times r+\dfrac{2}{3}\pi {{r}^{3}}=41\dfrac{19}{21}$ 

$\Rightarrow \pi {{r}^{3}}+\dfrac{2}{3}\pi {{r}^{3}}=\dfrac{880}{21}$

$\Rightarrow \dfrac{5}{3}\pi {{r}^{3}}=\dfrac{880}{21}$

$\Rightarrow {{r}^{3}}=\dfrac{880}{21}\times \dfrac{7}{22}\times \dfrac{3}{5}$

$\Rightarrow {{r}^{3}}=8$

$\Rightarrow r=2cm$

Since the internal diameter of the building is equal to its total height above the floor.

Therefore, the height of a building is $4cm$. 

8. The height of the Cone is $30$ cm. A small cone is cut of $f$ at the top by a plane parallel to its base if its volume is $\dfrac{1}{27}$ of the volume of the given cone at what height above the base is the section cut.

Ans: 

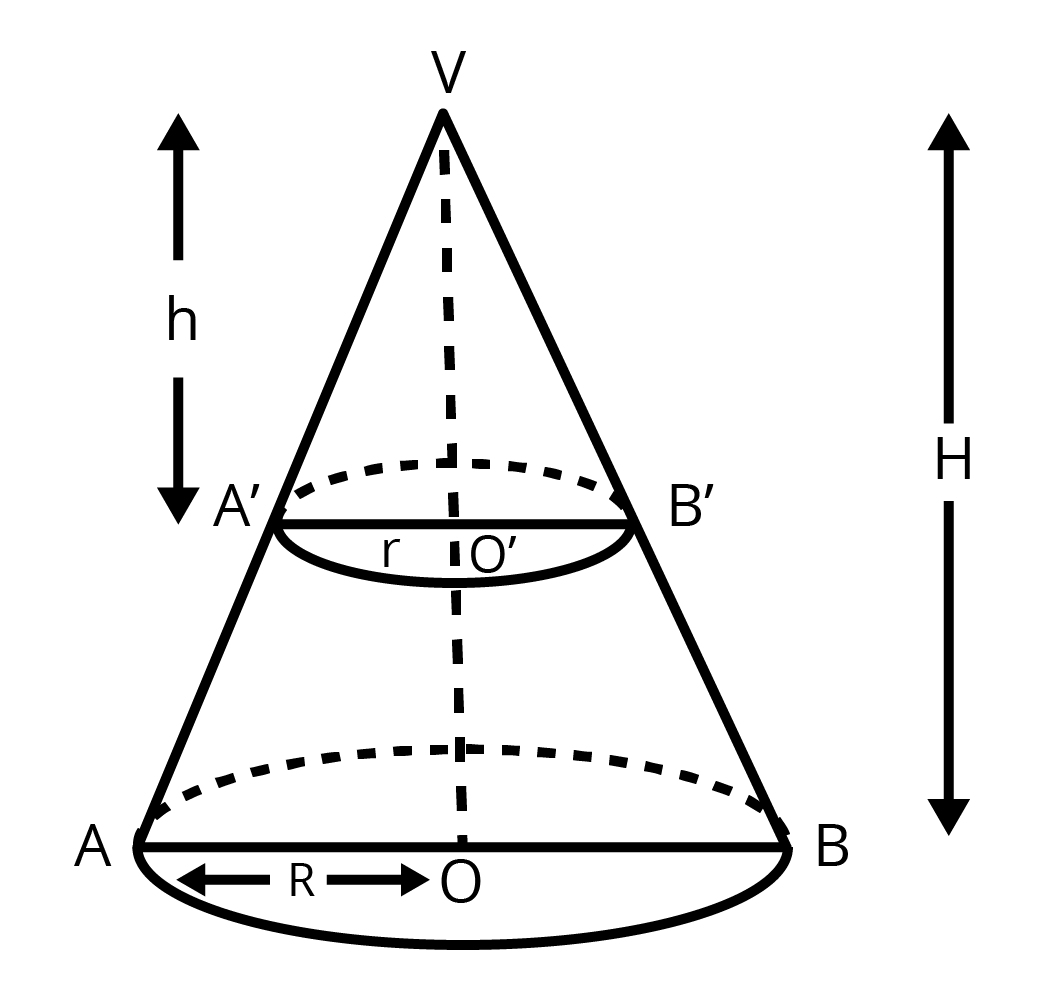
From the figure, 

$\Delta V{{O}^{'}}B\sim \Delta VOB$ 

We get

$\Rightarrow \dfrac{H}{h}=\dfrac{R}{r}$ 

$\Rightarrow \dfrac{30}{h}=\dfrac{R}{r}$ ….. (1)

$Volume\text{ }of\text{ }cone\text{ }V{{A}^{'}}{{B}^{'}}=\dfrac{1}{27}\left( \text{Volume of VAB} \right)$  

$\Rightarrow \dfrac{1}{3}\pi {{r}^{2}}h=\dfrac{1}{27}\left( \dfrac{1}{3}\pi {{R}^{2}}H \right)$

$\Rightarrow {{h}^{3}}=1000$

$\Rightarrow h=10cm$

Therefore, height at which section is made $\left( 30-10 \right)=20cm$. 

9. A hollow cone is cut by a plane parallel to the base and the upper portion is removed. If the curved surface of the remainder is $\dfrac{8}{9}th$ of the curved surface of the whole cone, find the ratio of the line segments into which the cone’s altitude is divided by the plane.

Ans: From the figure, 

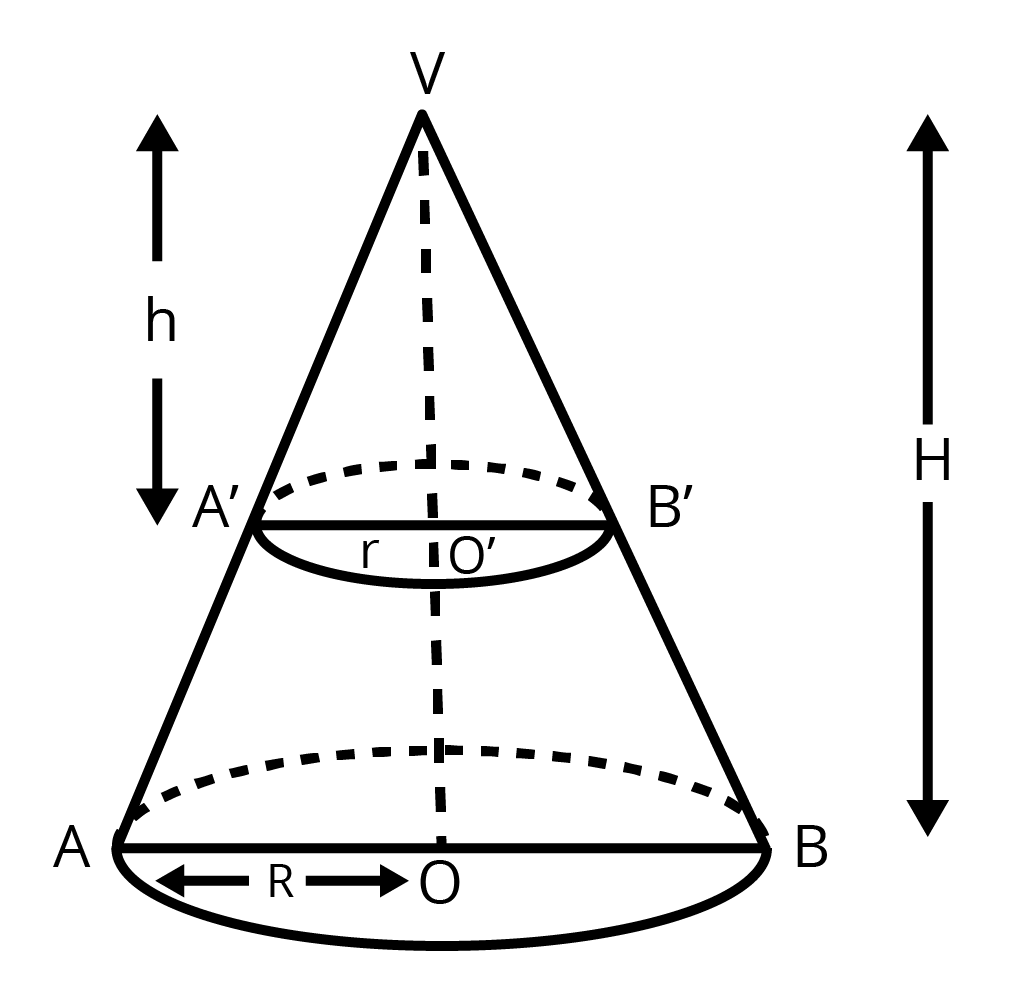
$\Delta V{{O}^{'}}B\sim \Delta VOB$ 

We get

$\Rightarrow \dfrac{H}{h}=\dfrac{R}{r}=\dfrac{l}{L}$ 

We get

\[\text{CSA of frustum}=\dfrac{8}{9}\left( \text{CSA of cone} \right)\] 

$\Rightarrow \left( \dfrac{R+r}{R} \right)\left( \dfrac{L-l}{L} \right)=\dfrac{8}{9}$ 

$\Rightarrow \left( 1+\dfrac{r}{R} \right)\left( 1-\dfrac{l}{L} \right)=\dfrac{8}{9}$

$\Rightarrow \left( 1+\dfrac{h}{H} \right)\left( 1-\dfrac{h}{H} \right)=\dfrac{8}{9}$

On simplifying we get

\[\Rightarrow {{1}^{2}}-{{\left( \dfrac{h}{H} \right)}^{2}}=\dfrac{8}{9}\]

\[\Rightarrow \dfrac{{{h}^{2}}}{{{H}^{2}}}=1-\dfrac{8}{9}\]

\[\Rightarrow \dfrac{{{h}^{2}}}{{{H}^{2}}}=\dfrac{1}{9}\]

\[\Rightarrow \dfrac{h}{H}=\dfrac{1}{3}\]

\[\Rightarrow H=3h\]

Therefore, required ratio will be $\dfrac{h}{H-h}=\dfrac{1}{2}$. 

10. Two right circular cones $X$ and $Y$ are made $X$ having $3$ times the radius of $Y$ and $Y$ having half the Volume of $X$. Calculate the ratio of heights of $X$ and $Y$.

Ans: Let the radius of cone one is $X=r$ 

Radius of second cone is $Y=3r$ 

Volume of $Y$ having half the Volume of $X$.

We get

$\Rightarrow \text{Volume of Y}=\text{ Volume of X}$ 

$\Rightarrow \dfrac{1}{3}\pi {{r}_{1}}^{2}{{h}_{2}}=\dfrac{1}{2}\left( \dfrac{1}{3}\pi {{r}_{2}}^{2}{{h}_{1}} \right)$ 

$\Rightarrow {{r}^{2}}{{h}_{2}}=\dfrac{1}{2}\left( 9{{r}^{2}}{{h}_{1}} \right)$

$\Rightarrow {{h}_{2}}=\dfrac{1}{2}\left( 9{{h}_{1}} \right)$

\[\Rightarrow \dfrac{{{h}_{1}}}{{{h}_{2}}}=\dfrac{2}{9}\]

Therefore, the ratio of heights of $X$ and $Y$ is $2:9$. 

11. If the areas of three adjacent faces of cuboid are $x,y,z$ respectively, Find the volume of the cuboids.

Ans: Given the areas of faces of cuboid are $x,y,z$.

Let $lb=x,bh=y,hl=z$ 

Volume of cuboid is $lbh$.

We get

$\Rightarrow {{V}^{2}}={{l}^{2}}{{b}^{2}}{{h}^{2}}$  

$\Rightarrow {{V}^{2}}=xyz$

$\therefore V=\sqrt{xyz}$

Therefore, volume of cuboids is $\sqrt{xyz}$. 

12. A shuttlecock used for playing badminton has the shape of a frustum of a cone mounted on a hemisphere. The external diameter of the frustum is $5$ cm and $2$ cm. The height of the entire shuttlecock is $7$ cm. Find the external surface area.

Ans: Given the diameters of a frustum of the cone are $5$ cm and $2$ cm.

So, radiuses are  ${{r}_{1}}=1cm$ and ${{r}_{2}}=2.5cm$ 

And the height of the shuttlecock is $7cm$. So the height of the cone is $h=7-1=6cm$ 

The external surface area of the shuttlecock is equal to the sum of the curved surface area of the cone and the surface area of the hemisphere.

We get

External surface area $=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l+2\pi r_{1}^{2}$ 

$\Rightarrow \pi \left( 2.5+1 \right)\sqrt{{{h}^{2}}+{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}}+2\pi \times 1$ 

\[\Rightarrow \pi \left( 3.5 \right)\sqrt{{{6}^{2}}+{{\left( 1-2.5 \right)}^{2}}}+2\pi \]

\[\Rightarrow \pi \left( 3.5 \right)\sqrt{36+2.25}+2\pi \]

\[\Rightarrow \pi \left( 3.5 \right)\sqrt{38.5}+2\pi \]

\[\Rightarrow \pi \left( 3.5 \right)6.18+2\pi \]

\[\Rightarrow 21.63\pi +2\pi \]

\[\Rightarrow 23.63\pi \]

\[\Rightarrow 23.63\times \dfrac{22}{7}\]

\[\Rightarrow 74.26c{{m}^{2}}\]

External surface area of shuttle cock is \[74.26c{{m}^{2}}\].

13. A conical vessel of radius $6cm$ and height $8cm$ is completely filled with water. A sphere is lowered into the water and its size is such that when it touches the sides, it is just immersed as shown in the figure. What fraction of water flows out?

Ans: let $r$ be the radius of the sphere.

By similarity property of triangles, we get

$\Rightarrow \dfrac{8-r}{10}=\dfrac{r}{6}$ 

$\Rightarrow 48-6r=10r$

$\Rightarrow 48=10r+6r$

$\Rightarrow 16r=48$

$\therefore r=3cm$

Now, fraction of water flows out will be

$\Rightarrow \text{Fraction of water overflows}=\dfrac{\text{Volume of sphere}}{\text{Volume of cone}}$ 

$\Rightarrow \text{Fraction of water overflows}=\dfrac{\dfrac{4}{3}\pi {{r}^{3}}}{\dfrac{1}{3}\pi {{r}^{2}}h}$

\[\Rightarrow \text{Fraction of water overflows}=\dfrac{\dfrac{4}{3}\pi {{\left( 3 \right)}^{3}}}{\dfrac{1}{3}\pi {{\left( 6 \right)}^{2}}8}\]

\[\Rightarrow \text{Fraction of water overflows}=\dfrac{4\pi {{\left( 3 \right)}^{3}}}{\pi {{\left( 6 \right)}^{2}}8}\]

\[\Rightarrow \text{Fraction of water overflows}=\dfrac{4\times 3\times 3\times 3\pi }{6\times 6\times 8\pi }\]

\[\Rightarrow \text{Fraction of water overflows}=\dfrac{3}{8}\]

Therefore, \[\dfrac{3}{8}\] fraction of water flows out.

14. A golf ball has a diameter equal to $4.1$ cm. Its surface has $150$ dimples each of radius $2$ mm. Calculate the total surface area which is exposed to the surroundings assuming that the dimples are hemispherical.

Ans: given the diameter of a golf ball is $4.1cm$ 

So the radius of golf ball is $\left( \dfrac{4.1}{2} \right)cm$ 

Surface area of ball is $4\pi {{r}^{2}}$.

We get

 $\Rightarrow 4\pi {{\left( \dfrac{4.1}{2} \right)}^{2}}=16.8\pi \text{ c}{{\text{m}}^{2}}$ 

Total surface area which is exposed to the surrounding will be

$\Rightarrow SA\text{ of ball}-150\times \pi {{r}^{2}}+150\times 2\pi {{r}^{2}}$ 

$\Rightarrow 16.8\pi -150\times \pi {{r}^{2}}+150\times 2\pi {{r}^{2}}$

$\Rightarrow 16.8\times 3.14+150\times 3.14{{\left( \dfrac{4.1}{2} \right)}^{2}}$

$\Rightarrow 71.68c{{m}^{2}}$

Therefore, the total surface area exposed to the surrounding is $71.68c{{m}^{2}}$.

15. A solid metallic circular cone $20cm$ height with a vertical angle of $60$ is cut into two parts at the middle point of its height by a plane parallel to the base. If the frustum, so obtained be drawn into a wire of diameter $\dfrac{1}{16}$ cm. Find the length of the wire.

Ans: Let ${{r}_{1}}$ and ${{r}_{2}}$ be the radii of lower and upper ends of a frustum cone.

We get

\[\Rightarrow \dfrac{{{r}_{1}}}{20}=\tan 30{}^\circ \] 

Then,

${{r}_{1}}=\dfrac{20}{\sqrt{3}}cm$ and ${{r}_{2}}=\dfrac{10}{\sqrt{3}}cm$ 

Height $=20cm$ 

Now, volume of frustum is

\[\Rightarrow \dfrac{1}{3}\pi \times 10\left[ {{\left( \dfrac{20}{\sqrt{3}} \right)}^{2}}+{{\left( \dfrac{10}{\sqrt{3}} \right)}^{2}}+\dfrac{20}{\sqrt{3}}\times \dfrac{10}{\sqrt{3}} \right]\] 

\[\Rightarrow \dfrac{1}{3}\pi \times 10\left[ \dfrac{400}{3}+\dfrac{100}{3}+\dfrac{200}{3} \right]\]

Since the frustum is drawn in to wire so the volumes of both are equal.

Let $l$ be the length of wire.

We get

\[\Rightarrow \dfrac{1}{3}\pi \times 10\left[ \dfrac{400}{3}+\dfrac{100}{3}+\dfrac{200}{3} \right]=\pi {{\left( \dfrac{1}{32} \right)}^{2}}\times l\]

\[\Rightarrow \dfrac{1}{3}\times 10\times \dfrac{700}{3}=\dfrac{1}{1024}\times l\]

\[\Rightarrow l=\dfrac{10\times 1024\times 700}{9}\]

\[\Rightarrow l=\dfrac{7168000}{9}\]

\[\therefore l=796444.4cm=7964.4m\]

Therefore, the length of wire is \[7964.4m\].

16. The lower portion of a haystack is an inverted cone frustum and the upper part is a cone that finds the total volume of the haystack.

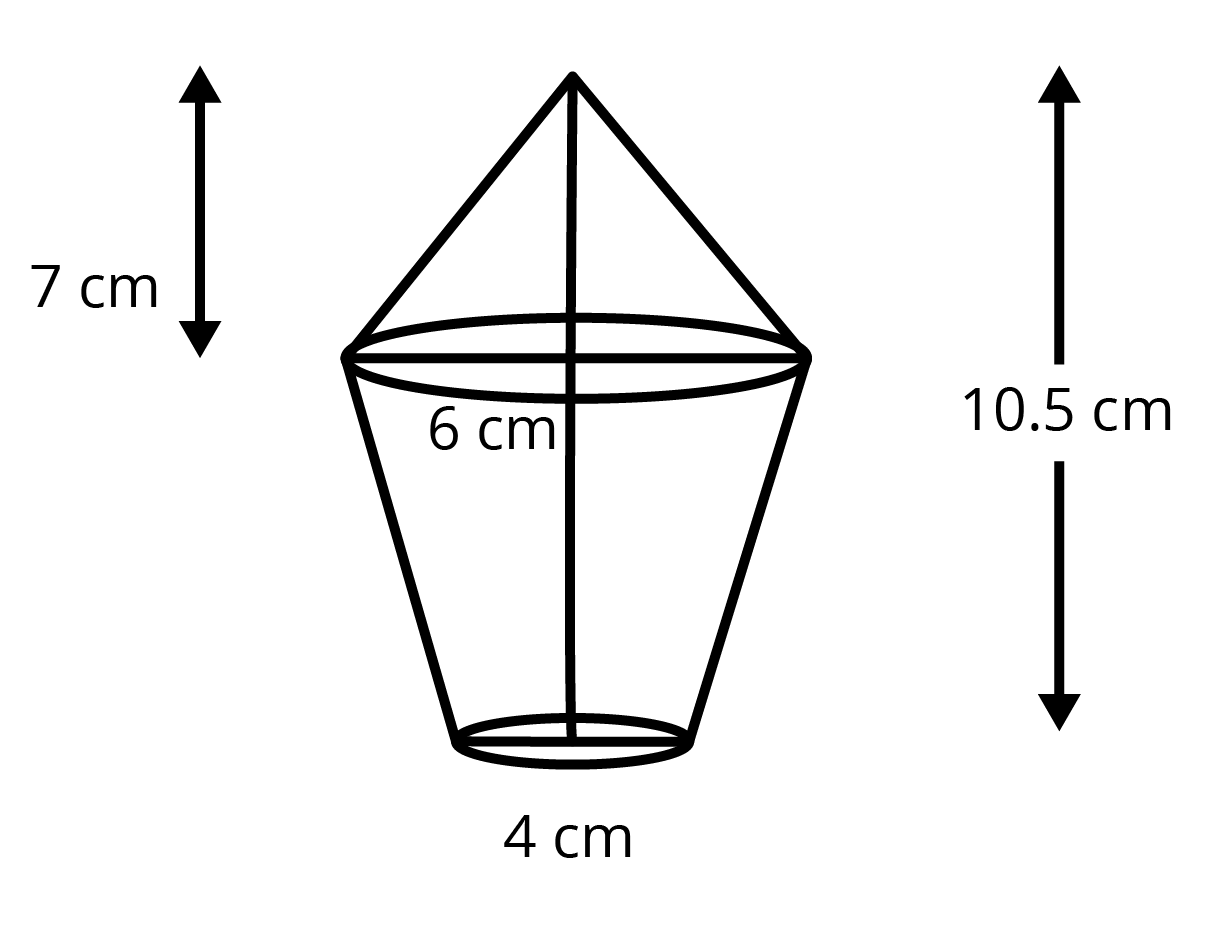
Ans: Let ${{r}_{1}}$ and ${{r}_{2}}$ be the radii of lower and upper ends of a frustum cone.

We get

${{r}_{1}}=3cm$ and ${{r}_{2}}=2cm$ 

Height $=\dfrac{7}{2}cm$ 

Now, volume of frustum is 

\[\Rightarrow \dfrac{1}{3}\pi \times \dfrac{7}{2}\left[ {{3}^{2}}+{{2}^{2}}+3\times 2 \right]\] 

\[\Rightarrow \dfrac{1}{3}\pi \times \dfrac{7}{2}\left[ 9+4+6 \right]\]

\[\Rightarrow \dfrac{1}{3}\pi \times \dfrac{7}{2}\times 19\]

\[\Rightarrow 22.16\pi \text{ c}{{m}^{3}}\]

Volume of cone is $\dfrac{1}{3}\pi {{\left( 3 \right)}^{2}}\times 7=21\pi \text{ c}{{\text{m}}^{3}}$ 

Now, volume of haystack is equal to the sum of volumes of cone and frustum.

We get

$\Rightarrow Total\text{ volume}=21\pi +22.16\pi $ 

$\Rightarrow Total\text{ volume}=43.16\times \dfrac{22}{7}$

$\therefore Total\text{ volume}=135.67c{{m}^{3}}$

Therefore, the volume of haystack is $135.67c{{m}^{3}}$.

17. A vessel in the shape of an inverted cone is surmounted by a cylinder that has a common radius of $7cm$ this was filled with liquid till it covered one third the height of the cylinder. If the height of each part is $9cm$ and the vessel is turned upside down. Find the volume of the liquid and to what height will it reach in the cylindrical part.

Ans: Given the radius of cone and cylinder are equal.

So, $r=7cm$ (for both cylinder and cone)

And $h=9cm$ (for both cylinder and cone)

Liquid is filled one third height of the cylinder.

Height of liquid in cylinder is $\dfrac{9}{3}=3cm$ 

Now, volume of liquid is equal to the sum of volume of cone and volume of cylinder from where liquid is filled.

We get

$\Rightarrow {{V}_{\left( l \right)}}=\dfrac{1}{3}\pi {{\left( 7 \right)}^{2}}\times 9+\pi {{\left( 7 \right)}^{2}}\times 3$ 

$\Rightarrow {{V}_{\left( l \right)}}=\dfrac{1}{3}\pi \times 49\times 9+\pi \times 49\times 3$

$\Rightarrow {{V}_{\left( l \right)}}=147\pi +147\pi $

$\therefore {{V}_{\left( l \right)}}=294\pi \text{ c}{{\text{m}}^{3}}$

Since the vessel turned upside down

The height of cylindrical part is

$\Rightarrow \dfrac{294\pi }{49\pi }=6cm$ 

Therefore, the liquid reaches $6cm$high in the cylindrical part.

1 Marks Questions

1. A metallic sphere of radius $10.5cm$ is melted and then recast into small cones each of radius $3.5cm$ and height $3cm$, the number of such cones is

(a)  $63$

(b)  $126$

(c)  $21$ 

(d)  $130$

Ans: Given metallic sphere is melted and recast into small cones.

$\therefore \text{Number of cones}=\dfrac{\text{Volume of sphere}}{\text{Volume of cone}}$

$\Rightarrow \text{Number of cones}=\dfrac{\dfrac{4}{3}\pi {{r}^{3}}}{\dfrac{1}{3}\pi {{R}^{2}}h}$

$\Rightarrow \text{Number of cones}=\dfrac{4{{\left( 10.5 \right)}^{3}}}{{{\left( 3.5 \right)}^{2}}\times 3}$

$\Rightarrow \text{Number of cones}=\dfrac{4630.5}{36.75}$

$\therefore \text{Number of cones}=126$

Therefore, option (b) is correct answer.

2. A solid sphere of radius $r$ is melted and cast into the shape of a solid cone of height $r$, the radius of the base of the cone is

(a)  $2r$

(b)  $3r$

(c)   $r$

(d)  $4r$

Ans: Let $R$ be the radius of the base of the cone.

The solid sphere is melted and recast into the shape of a solid cone.

So volumes of both are equal.

We get

$\Rightarrow \dfrac{1}{3}\pi {{R}^{2}}h=\dfrac{4}{3}\pi {{r}^{3}}$

$\Rightarrow \dfrac{1}{3}\pi {{R}^{2}}\times r=\dfrac{4}{3}\pi {{r}^{3}}$

\[\Rightarrow {{R}^{2}}=4{{r}^{2}}\]

\[\therefore R=2r\]

Therefore, option (a) is the correct answer.

3. During the conversion of a solid from one shape to another, the volume of the new shape will

(a)  Increase

(b)  Decrease

(c)   Remain unaltered

(d)  Be doubled

Ans: (c) Remain unaltered

4. A right circular cylinder of radius $r$ cm and height $h$ cm $\left( h>2r \right)$ just encloses a sphere of diameter

(a)  $r$ cm

(b)  $2r$ cm

(c)   $h$ cm

(d)  $2h$ cm

Ans: The diameter of the sphere is equal to the diameter of the base of the cylinder.

Given that the radius of cylinder is $r$ so the diameter of sphere will be $2r\text{ }cm$.

Therefore, option (b) is the correct answer.

5. A solid sphere of radius $r$ is melted and cast into the shape of a solid cone of height $r$, the radius of the base of the cone is

(a)  $2r$

(b)  $3r$

(c)   $r$

(d)  $4r$

Ans: Let $R$ be the radius of the base of the cone.

The solid sphere is melted and recast into the shape of a solid cone.

So volumes of both are equal.

We get

$\Rightarrow \dfrac{1}{3}\pi {{R}^{2}}h=\dfrac{4}{3}\pi {{r}^{3}}$

$\Rightarrow \dfrac{1}{3}\pi {{R}^{2}}\times r=\dfrac{4}{3}\pi {{r}^{3}}$

\[\Rightarrow {{R}^{2}}=4{{r}^{2}}\]

\[\therefore R=2r\]

Therefore, option (a) is the correct answer.

6. A reservoir is in the shape of a frustum of a right circular cone. It is $8$ m across at the top and $4$ m across at the bottom. If it is $6$ m deep, then its capacity is

(a)  $176{{m}^{3}}$

(b)  $196{{m}^{3}}$

(c)   $200{{m}^{3}}$

(d)  $110{{m}^{3}}$

Ans: Given a reservoir is in the shape of a frustum of a cone.

So the volume of reservoir is \[\dfrac{1}{3}\pi h\left[ r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right]\]

\[\Rightarrow \dfrac{1}{3}\times \dfrac{22}{7}\times 6\left[ {{4}^{2}}+{{2}^{2}}+4\times 2 \right]\]

\[\Rightarrow \dfrac{1}{3}\times \dfrac{22}{7}\times 6\left[ 16+4+8 \right]\]

\[\Rightarrow \dfrac{1}{3}\times \dfrac{22}{7}\times 6\times 28\]

\[\Rightarrow 22\times 2\times 4\]

$\Rightarrow 176{{m}^{3}}$

Therefore, option (a) is the correct answer.

7. A cone of height $24$ cm and radius of base $6$ cm is made up of modelling clay. A child reshapes it in the form of a sphere, the radius of the sphere is

(a)  $5$ cm

(b)  $6$ cm

(c)   $8$ cm

(d)  $12$ cm

Ans: Let $R$ be the radius of the sphere.

Cone is moulded and recast into the shape of a sphere.

So volumes of both are equal.

We get

$\Rightarrow \dfrac{1}{3}\pi {{r}^{2}}h=\dfrac{4}{3}\pi {{R}^{3}}$

$\Rightarrow \dfrac{1}{3}\pi {{\left( 6 \right)}^{2}}\times 24=\dfrac{4}{3}\pi {{R}^{3}}$

$\Rightarrow 36\times 24=4{{R}^{3}}$

$\Rightarrow 9\times 24={{R}^{3}}$

$\Rightarrow {{R}^{3}}=216$

\[\therefore R=6\]

Therefore, option (b) is the correct answer.

8. A circular tent is cylindrical to a height of $4$ m and conical above it. If its diameter is $210$ m and its slant height is $40$ m. The total area of the canvas required in ${{m}^{2}}$ is

(a)  $1760$

(b)  $15840$

(c)   $3960$

(d)  $7960$

Ans: Total surface area of the canvas required is the sum of curved surface area of the cylindrical part and curved surface area of the conical cap.

We get,

$TSA=2\pi rh+\pi rl$

$\Rightarrow TSA=2\pi \times 105\times 4+\pi \times 105\times 40$

$\Rightarrow TSA=840\pi +4200\pi $

$\Rightarrow TSA=5040\pi $

$\Rightarrow TSA=5040\times \dfrac{22}{7}$

$\therefore TSA=15840{{m}^{2}}$

Therefore, option (b) is the correct answer.

9. The radii of the ends of a bucket $30$ cm high are $21$ cm and $7$ cm. then its capacity in litres is

(a)  $19.02$

(b)  $20.02$

(c)   $21.02$

(d)  $19.08$

Ans: Capacity of bucket is equal to the volume of bucket, we get

\[\Rightarrow \dfrac{1}{3}\pi h\left[ r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right]\]

\[\Rightarrow \dfrac{1}{3}\pi \times 30\left[ {{21}^{2}}+{{7}^{2}}+21\times 7 \right]\]

\[\Rightarrow \dfrac{1}{3}\pi \times 30\left[ 441+49+147 \right]\]

\[\Rightarrow \dfrac{1}{3}\pi \times 30\times 637\]

\[\Rightarrow \dfrac{22}{7}\times 6370c{{m}^{3}}\]

\[\Rightarrow 20020c{{m}^{3}}=~20.02liters\]

Therefore, option (b) is the correct answer.

10. A solid is hemispherical at the bottom and conical above it. The surface areas of the two parts are equal, then the ratio of its radius and the height of its conical part is

(a)  $1:3$

(b)  $1:\sqrt{3}$

(c)   $1:1$

(d)  $\sqrt{3}:1$

Ans: Given that surface areas of hemispherical part and conical part are equal.

We get

$\Rightarrow 2\pi {{r}^{2}}=\pi rl$

$\Rightarrow 2r=l$

$\Rightarrow 2r=\sqrt{{{r}^{2}}+{{h}^{2}}}$

$\Rightarrow 4{{r}^{2}}={{r}^{2}}+{{h}^{2}}$

$\Rightarrow 3{{r}^{2}}={{h}^{2}}$

$\Rightarrow \dfrac{{{r}^{2}}}{{{h}^{2}}}=\dfrac{1}{3}$

$\therefore \dfrac{r}{h}=\dfrac{1}{\sqrt{3}}$

$\therefore r:h=1:\sqrt{3}$

Therefore, (b) is the correct answer.

11. The diameter of a sphere is $6$ cm. It is melted and drawn into a wire of diameter $2$ cm. The length of the wire is

(a)  $12$ cm

(b)  $18$ cm

(c)   $36$ cm

(d)  $66$ cm

Ans: Given the diameter of a sphere is $6$ cm.

So, radius of sphere $r=\dfrac{6}{2}=3cm$

Since volume of sphere is equal to the volume of wire.

We get

 $\Rightarrow \dfrac{4}{3}\pi {{r}^{3}}=\pi {{r}^{2}}h$

$\Rightarrow \dfrac{4}{3}{{\left( 3 \right)}^{3}}={{\left( 1 \right)}^{2}}h$

$\Rightarrow \dfrac{4}{3}\times 3\times 3\times 3=h$

$\Rightarrow h=36cm$

Therefore, option (c) is the correct answer.

12. If the radii of the circular ends of a bucket of height $40$ cm are $35$ cm and $14$ cm. Then volume of the bucket in cubic centimeters is

(a)  $60060$

(b)  $80080$

(c)   $70040$

(d)  $80760$

Ans: The volume of bucket is

\[\Rightarrow \dfrac{1}{3}\pi h\left[ r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right]\]

\[\Rightarrow \dfrac{1}{3}\pi \times 40\left[ {{35}^{2}}+{{14}^{2}}+35\times 14 \right]\]

\[\Rightarrow \dfrac{1}{3}\pi \times 40\left[ 1225+196+490 \right]\]

\[\Rightarrow \dfrac{1}{3}\pi \times 40\times 1911\]

\[\Rightarrow \dfrac{22}{7}\times 40\times 637c{{m}^{3}}\]

\[\Rightarrow 80080c{{m}^{3}}\]

Therefore, option (b) is the correct answer.

13. The diameter of a metallic sphere is $6$ cm. It is melted and drawn into a wire of diameter of the cross-section $0.2$ cm, then the length of wire is

(a)  $12m$

(b)  $18m$

(c)   $36m$

(d)  $66m$

Ans: Given the diameter of a sphere is $6$ cm.

So, radius of sphere $r=\dfrac{6}{2}=3cm$

Since volume of sphere is equal to the volume of wire.

We get

 $\Rightarrow \dfrac{4}{3}\pi {{r}^{3}}=\pi {{r}^{2}}h$

$\Rightarrow \dfrac{4}{3}{{\left( 3 \right)}^{3}}={{\left( 0.1 \right)}^{2}}h$

$\Rightarrow \dfrac{4}{3}\times 3\times 3\times 3=0.01h$

$\Rightarrow h=3600cm=36m$

Therefore, option (c) is the correct answer.

14. The ratio between the volumes of two spheres is $8:27$. What is the ratio between their surface areas?

(a)  $2:3$

(b)  $4:5$

(c)   $5:6$

(d)  $4:9$

Ans: Given that

$\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{8}{27}$

$\Rightarrow \dfrac{\dfrac{4}{3}\pi {{r}_{1}}^{3}}{\dfrac{4}{3}\pi {{r}_{2}}^{3}}=\dfrac{8}{27}$

$\Rightarrow \dfrac{{{r}_{1}}}{{{r}_{2}}}=\dfrac{2}{3}$

Thus, $\dfrac{{{S}_{1}}}{{{S}_{2}}}=\dfrac{4\pi {{r}_{1}}^{2}}{4\pi {{r}_{1}}^{2}}$

$\Rightarrow \dfrac{{{S}_{1}}}{{{S}_{2}}}=\dfrac{{{r}_{1}}^{2}}{{{r}_{1}}^{2}}$

$\Rightarrow \dfrac{{{S}_{1}}}{{{S}_{2}}}=\dfrac{4}{9}$

Therefore, option (d) is the correct answer.

15. A hollow cube of internal edge $22$ cm is filled with spherical marbles of diameter $0.5$ cm and it is assumed that $\dfrac{1}{8}$ space of the cube remains unfilled. Then the number of marbles that the cube can accommodate is

(a)  $142296$

(b)  $142396$

(c)   $142496$

(d)  $142596$

Ans: $\therefore \text{Number of marbles}=\dfrac{\text{space of cube occupied by marbles}}{\text{Volume of each marble}}$

\[\Rightarrow \text{Number of marbles}=\dfrac{{{l}^{3}}-\dfrac{1}{8}{{l}^{3}}}{\dfrac{4}{3}\pi {{r}^{3}}}\]

\[\Rightarrow \text{Number of marbles}=\dfrac{{{\left( 22 \right)}^{3}}-\dfrac{1}{8}{{\left( 22 \right)}^{3}}}{\dfrac{4}{3}\pi {{\left( \dfrac{0.5}{2} \right)}^{3}}}\]

\[\Rightarrow \text{Number of marbles}=\dfrac{10648-\dfrac{1}{8}\times 10648}{\dfrac{4}{3}\pi {{\left( \dfrac{1}{4} \right)}^{3}}}\]

\[\Rightarrow \text{Number of marbles}=\dfrac{10648-1331}{\dfrac{4}{3}\times \dfrac{22}{7}\times \dfrac{1}{4}\times \dfrac{1}{4}\times \dfrac{1}{4}}\]

\[\Rightarrow \text{Number of marbles}=\dfrac{9317}{\dfrac{22}{336}}\]

\[\Rightarrow \text{Number of marbles}=\dfrac{336}{22}\times 9317\]

\[\therefore \text{Number of marbles}=142296\]

Therefore, option (a) is the correct answer.

2 Marks Questions

Unless stated otherwise, take $\pi =\dfrac{22}{7}$. 

1. $2$ cubes each of volume $64c{{m}^{3}}$ are joined end to end. Find the surface area of the resulting cuboid.

Ans: Abbreviation: CSA = Curved Surface Area TSA = Total Surface Area

V = Volume

We know that the volume of cube is given by ${{\left( side \right)}^{3}}$ 

Now, as given in the question, ${{\left( side \right)}^{3}}=64$

We can write

$\Rightarrow {{\left( side \right)}^{3}}={{4}^{3}}$

$\Rightarrow side=4cm$

So, for the resulting cuboid,

$length\left( l \right)=4+4=8cm$ 

$breadth\left( b \right)=4cm$

$height\left( h \right)=4cm$

Now, surface area of resulting cuboid $=2\left( lb+bh+hl \right)$ 

Substituting values, we get

$\Rightarrow \text{surface area }=2\left( 8\times 4+4\times 4+4\times 8 \right)$ 

$\Rightarrow \text{surface area }=2\left( 32+16+32 \right)$

$\Rightarrow \text{surface area }=2\times 80$

$\therefore \text{surface area }=160c{{m}^{2}}$

2. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to $1$ cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of $\pi $. 

Ans: Abbreviation: CSA = Curved Surface Area, TSA = Total Surface Area,

V = Volume

For hemisphere, Radius $r=1cm$ 

Volume$=\dfrac{2}{3}\pi {{r}^{3}}$ 

\[\Rightarrow Volume=\dfrac{2}{3}\pi {{\left( 1 \right)}^{3}}\] 

\[\Rightarrow Volume=\dfrac{2}{3}\pi \text{ }c{{m}^{3}}\]

For cone, Radius of the base $r=1cm$ and height$r=1cm$

So, Volume $=\dfrac{1}{3}\pi {{r}^{2}}h$

\[\Rightarrow Volume=\dfrac{1}{3}\pi {{\left( 1 \right)}^{2}}\times 1\] 

\[\Rightarrow Volume=\dfrac{1}{3}\pi \text{ }c{{m}^{3}}\]

$\therefore Volume\text{ }of\text{ }the\text{ }solid=Volume\text{ }of\text{ }hemisphere+Volume\text{ }of\text{ }cone$ 

\[\Rightarrow Volume\text{ of the solid}=\dfrac{2}{3}\pi +\dfrac{1}{3}\pi \]

\[\therefore Volume\text{ of the solid}=\pi c{{m}^{3}}\]

3. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are $15$ cm by $10$ cm by $3.5$ cm. The radius of each of the depressions is $0.5$ cm and the depth is $1.4$ cm. Find the volume of wood in the entire stand (see figure).

Ans: We know that volume of the cuboid $=l\times b\times h$ 

Given dimensions of the cuboid are $15cm\times 10cm\times 3.5cm$ 

So the volume of cuboid is

$\Rightarrow 15\times 10\times 3.5$ 

$\Rightarrow 525c{{m}^{3}}$

Now, volume of conical depression $=\dfrac{1}{3}\pi {{r}^{2}}h$

\[\Rightarrow Volume=\dfrac{1}{3}\times \dfrac{22}{7}\times 0.5\times 0.5\times 1.4\] 

\[\Rightarrow Volume=\dfrac{11}{30}c{{m}^{3}}\]

Now, volume of four conical depressions \[=4\times \dfrac{11}{30}=1.47c{{m}^{3}}\]

$\therefore $ Volume of the wood in the entire stand $=525-1.47=523.53c{{m}^{3}}$ 

4. A metallic sphere of radius $4.2$ cm is melted and recast into the shape of a cylinder of radius $6$ cm. Find the height of the cylinder.

Ans: Abbreviation: CSA = Curved Surface Area TSA = Total Surface Area

V = Volume

For sphere, Radius $r=4.2cm$ 

So, Volume$=\dfrac{4}{3}\pi {{r}^{3}}$ 

\[\Rightarrow Volume=\dfrac{4}{3}\pi {{\left( 4.2 \right)}^{3}}c{{m}^{3}}\] 

For cylinder, Radius $R=6cm$

Let the height of the cylinder be $H$ cm.

Then, Volume of cylinder is $\pi {{R}^{2}}H$ 

\[\Rightarrow Volume=\pi {{\left( 6 \right)}^{2}}H\text{ }c{{m}^{3}}\]

Now, as given in the question, Volume of sphere =Volume of cylinder

So, we get

$\Rightarrow \dfrac{4}{3}\pi {{r}^{3}}=\pi {{R}^{2}}H$

$\Rightarrow \dfrac{4}{3}\pi {{\left( 4.2 \right)}^{3}}=\pi {{\left( 6 \right)}^{2}}H$

$\Rightarrow H=\dfrac{4{{\left( 4.2 \right)}^{3}}}{3{{\left( 6 \right)}^{2}}}$

$\therefore H=2.74cm$

Therefore, the height of cylinder is $2.74cm$.

5. Metallic spheres of radii $6$ cm, $8$ cm and $10$ cm respectively are melted to form a single solid sphere. Find the radius of the resulting sphere.

Ans: Let the radius of resulting sphere be $r\text{ }cm$.

As given in the question three metallic spheres melted and formed a single solid sphere.

So volume of resulting sphere is equal to the sum of volume of three spheres.

We get

$\Rightarrow \dfrac{4}{3}\pi {{r}^{3}}=\dfrac{4}{3}\pi {{\left( 6 \right)}^{3}}+\dfrac{4}{3}\pi {{\left( 8 \right)}^{3}}+\dfrac{4}{3}\pi {{\left( 10 \right)}^{3}}$ 

$\Rightarrow {{r}^{3}}={{\left( 6 \right)}^{3}}+{{\left( 8 \right)}^{3}}+{{\left( 10 \right)}^{3}}$

$\Rightarrow {{r}^{3}}=216+512+1000$

$\Rightarrow {{r}^{3}}=1728$

$\therefore r=12cm$

Therefore, radius of resulting sphere is $12cm$.

6. A $20$ m deep well with a diameter of $7$m is dug and the earth from digging is evenly spread out to form a platform of $22$ m by $14$ m. Find the height of the platform.

Ans: Given, Diameter of well $=7m$ 

So, the radius of well $r=\dfrac{7}{2}m$

And Depth of earth dug $h=20m$ 

Given, the earth from digging is evenly spread out.

So, Length of platform $l=22m$, and Breadth of platform $b=14m$ 

Let height of the platform be $h$ 

So, according to question,

Volume of earth dug =Volume of platform

We get,

$\Rightarrow \pi {{r}^{2}}h=l\times b\times h$ 

$\Rightarrow \dfrac{22}{7}\times \dfrac{7}{2}\times \dfrac{7}{2} \times 20 =22\times 14\times h$

$\Rightarrow h=\dfrac{22\times 7\times 7 \times 20}{7\times 2\times 2\times 22\times 14}$

$\therefore h=2.5 m$

Therefore, the height of platform is $2.5 m$.

7. A well of diameter $3$ m is dug $14$ m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width $4$ m to form an embankment. Find the height of the embankment.

Ans: Given, Diameter of well $=3m$ 

So, the radius of well $r=\dfrac{3}{2}m$

And Depth of earth dug $h=14m$ 

Given, the earth from digging is evenly spread out.

Radius of the embankment $r=\dfrac{3}{2}+4$ =$\dfrac{11}{2} m$

Let height of the embankment be $h$ 

So, according to question,

Volume of earth embankment  =Volume of earth dug

We get,

$\Rightarrow \pi {({{r_1}}^2- {r_2}^{2}  )}h= \pi r^2 h$

$\Rightarrow  {[ {(\dfrac{11}{2})}^2- {(\dfrac{3}{2})}^{2} ]}h^\prime=  ({\dfrac{3}{2})}^2 \times 14$

$[\dfrac{121}{4}-\dfrac{9}{4}] h^\prime=\dfrac{9}{4} \times 14$

$\dfrac{112}{4} h^\prime=\dfrac{9}{4} \times 14$

$h^\prime= \dfrac{9 \times 14 \times 4}{112\times 4}$

$\therefore h^\prime = 1.125cm$

Therefore, the height of embankment is $1.125cm$.

8. A container shaped like a right circular cylinder having a diameter of $12$ cm and a height of $15$ cm is full of ice cream. The ice cream is to be filled into cones of height $12$ cm and diameter $6$ cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.

Ans: For right circular cylinder, given the diameter $=12cm$ 

So, radius $=6cm$ and height $=15cm$ 

For cone, given the diameter $=6cm$ 

So, radius $=3cm$ and height $=15cm$ 

Let $n$ cones be filled with ice cream.

Then, according to the question,

$n$ (Volume of cones + volume of hemisphere) =Volume of right circular cylinder

We get

$\Rightarrow n(\dfrac{1}{3}\pi {{r}^{2}}h + \dfrac{2}{3}\pi {{r}^{3}}) =\pi {{r}^{2}}h$ 

\[\Rightarrow n(\dfrac{1}{3}\times \dfrac{22}{7}\times {{\left( 3 \right)}^{2}}\times 12 + \dfrac{2}{3}\times\pi\times {{3}^{3}})=\dfrac{22}{7}\times {{\left( 6 \right)}^{2}}\times 15\]

\[\Rightarrow n=\dfrac{6\times 6\times 15}{3\times 12 + 18}\]

\[\Rightarrow n=10\]

Therefore, $10$ cones will be filled with ice cream.

9. How many silver coins, $1.75$ cm in diameter and of thickness $2$ mm, must be melted to form a cuboid of dimensions \[\mathbf{5}.\mathbf{5cm}\times \mathbf{10cm}\times \mathbf{3}.\mathbf{5cm}\]?

Ans: Given, 

For silver coin, diameter is $1.75cm$ so radius is $\dfrac{1.75}{2}cm$ 

Thickness/height $=2mm=\dfrac{1}{5}cm$ 

For cuboid, dimensions are $5.5cm\times 10cm\times 3.5cm$ 

As given in the question silver coins are melted and formed a cuboid.

So the volume of coins is equal to the volume of cuboids.

Let the number of silver coins is $n$.

We get

$\Rightarrow n\times \pi {{r}^{2}}h=l\times b\times h$ 

$\Rightarrow n\times \dfrac{22}{7}{{\left( \dfrac{7}{8} \right)}^{2}}\times \dfrac{1}{5}=5.5\times 10\times 3.5$

$\Rightarrow n\times \dfrac{22}{7}\times \dfrac{49}{64}\times \dfrac{1}{5}=5.5\times 10\times 3.5$

$\Rightarrow n=\dfrac{5.5\times 10\times 3.5\times 7\times 64\times 5}{22\times 49}$

$\therefore n=400$

Therefore, $400$ silver coins must be melted.

10. A drinking glass is in the shape of a frustum of a cone of height $14$ cm. The diameters of its two circular ends are $4$ cm and $2$ cm. Find the capacity of the glass.

Ans: Abbreviation: CSA = Curved Surface Area

TSA = Total Surface Area

V = Volume

Given the diameter of two ends of a frustum cone are $4$ cm and $2$ cm.

So the radiuses are

${{r}_{1}}=1cm$ and ${{r}_{2}}=2cm$ 

Height $=14cm$ 

Now, capacity of glass is

\[\Rightarrow \dfrac{\pi h}{3}\left[ r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right]\] 

\[\Rightarrow \dfrac{22}{7}\times \dfrac{14}{3}\left[ {{1}^{2}}+{{2}^{2}}+2 \right]\]

\[\Rightarrow \dfrac{44}{3}\left[ 1+4+2 \right]\]

\[\Rightarrow \dfrac{44}{3}\times 7\]

\[\Rightarrow \dfrac{308}{3}\] 

\[\therefore \text{Capacity of glass}=102\dfrac{2}{3}\]

11. The slant height of a frustum of a cone is $4$ cm and the perimeters (circumference) of its circular ends are $18$ cm and $6$ cm. Find the curved surface area of the frustum.

Ans: Let ${{r}_{1}}$ and ${{r}_{2}}$ be the radii of the ends of the frustum of the cone.

Slant height of cone is $l=4cm$ 

Given the circumference of circular ends are $18cm$ and $6cm$.

We get

$\Rightarrow 2\pi {{r}_{1}}=18cm$ 

$\Rightarrow \pi {{r}_{1}}=9cm$ and

$\Rightarrow 2\pi {{r}_{2}}=6cm$ 

$\Rightarrow \pi {{r}_{2}}=3cm$

Curved surface area of frustum is $=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l$

$\Rightarrow \text{Curved surface area}=\left( \pi {{r}_{1}}+\pi {{r}_{2}} \right)l$ 

$\Rightarrow \text{Curved surface area}=\left( 9+3 \right)4$

$\therefore \text{Curved surface area}=48c{{m}^{2}}$

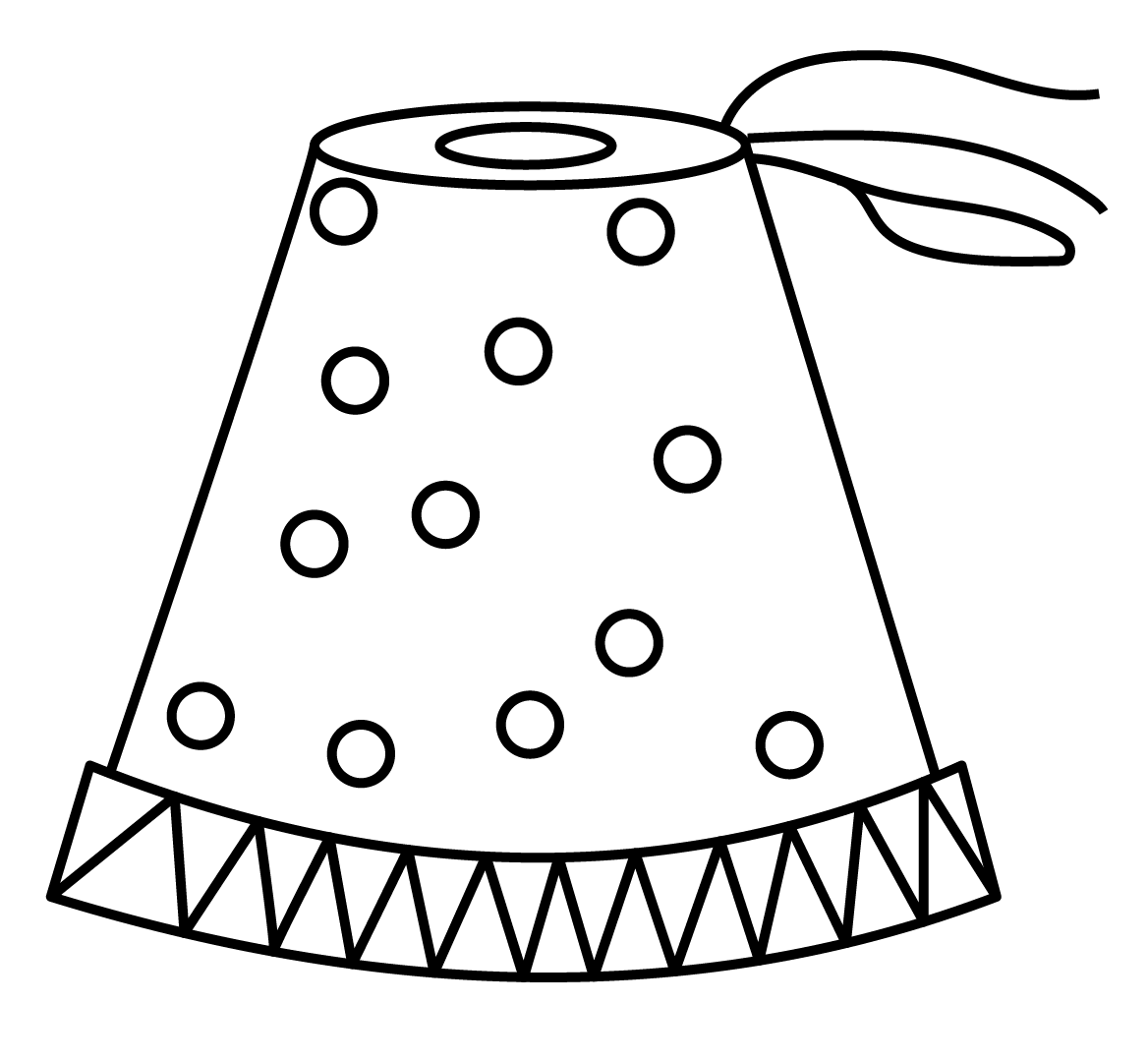
12. A fez, the cap used by the Turks, is shaped like the frustum of a cone (see figure). If its radius on the open side is $10$ cm, the radius at the upper base is $4$ cm and its slant height is $15$ cm, find the area of material used for making it.

Ans: Given the radiuses of two ends of a frustum cone are $10$ cm and $4$ cm.

So the radiuses are

${{r}_{1}}=10cm$ and ${{r}_{2}}=4cm$ 

Height $l=15cm$ 

Surface area $=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l+\pi r_{2}^{2}$ 

\[\Rightarrow \text{Surface area}=\dfrac{22}{7}\times \left( 10+4 \right)\times 15+\dfrac{22}{7}\times {{\left( 4 \right)}^{2}}\]

$\Rightarrow \text{Surface area}=660+\dfrac{352}{7}$

$\Rightarrow \text{Surface area}=\dfrac{4972}{7}$

$\therefore \text{Surface area}=710\dfrac{2}{7}c{{m}^{2}}$

13. A container opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height $16$ cm with radii of its lower and upper ends as $8$ cm and $20$ cm respectively. Find the total cost of milk which can completely fill the container at the rate of Rs. $20$ per litre. Also find the cost of the metal sheet used to make the container, if it costs Rs. $8\text{ per }100c{{m}^{2}}$.

Ans: Given the radiuses of two ends of a frustum cone are $8$ cm and $20$ cm.

So the radiuses are

${{r}_{1}}=20cm$ and ${{r}_{2}}=8cm$ 

Height $=16cm$ 

Now, volume of container is 

\[\Rightarrow \dfrac{1}{3}\pi h\left[ r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right]\] 

\[\Rightarrow \dfrac{1}{3}\times 3.14\times 16\left[ {{20}^{2}}+{{8}^{2}}+20\times 8 \right]\]

\[\Rightarrow \dfrac{1}{3}\times 3.14\times 16\left[ 400+64+160 \right]\]

\[\Rightarrow \dfrac{1}{3}\times 3.14\times 16\times 624\]

\[\Rightarrow 10449.92c{{m}^{2}}=10.44992liters\] 

The total cost of milk is $10.44992\times 20=208.8894$ 

The cost of milk is $Rs.209$ 

Surface area $=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l+\pi r_{2}^{2}$ 

$\Rightarrow \text{Surface area}=\pi \left( {{r}_{1}}+{{r}_{2}} \right)\sqrt{{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}+{{h}^{2}}}+\pi r_{2}^{2}$

$\Rightarrow \text{Surface area}=3.14\left( 20+8 \right)\sqrt{{{\left( 20-8 \right)}^{2}}+{{16}^{2}}}+3.14{{\left( 8 \right)}^{2}}$

$\Rightarrow \text{Surface area}=3.14\times 28\sqrt{144+256}+3.14\times 64$

$\Rightarrow \text{Surface area}=1158+200.96$

$\therefore \text{Surface area}=1959.36c{{m}^{2}}$

Cost of metal sheet is $8\text{ per }100c{{m}^{2}}$.

Total cost of metal sheet is $1959.36\times \dfrac{8}{100}=156.7488$ 

Therefore, cost of metal sheet is $Rs.156.75$. 

14. A copper wire, $3$ mm in diameter is wound about a cylinder whose length is $12$ cm and diameter $10$ cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be $8.88\text{ }g\text{ }per\text{ }c{{m}^{3}}$.

Ans: Abbreviation: CSA = Curved Surface Area

TSA = Total Surface Area

V = Volume

Given the length of cylinder is $12cm$, i.e. $120mm$.

Number of rounds to cover $120mm$ is $\dfrac{120}{3}=40$ 

Length of wire in completing one round is $2\pi r=10\pi cm$ 

So, length of the wire in completing $40$ rounds is $10\pi \times 40=400\pi cm$

Radius of copper wire is $\dfrac{3}{2}mm=\dfrac{3}{20}cm$ 

Volume of wire is $\pi {{\left( \dfrac{3}{20} \right)}^{2}}\left( 400\pi  \right)$ .

$\therefore Volume=9\pi \text{ }c{{m}^{3}}$ 

Given the density of copper is $8.88\text{ }g\text{ }per\text{ }c{{m}^{3}}$.

Mass of wire is $9\times {{\left( 3.14 \right)}^{2}}\times 8.88$ 

$\therefore Mass=787.98g$. 

15. A right triangle, whose sides are $3$ cm and $4$ cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose a value of $\pi $ as found appropriate)

Ans: Given the sides of triangle are $3$ cm and $4$ cm. 

Hypotenuse of triangle is $\sqrt{{{3}^{2}}+{{4}^{2}}}=5cm$ 

From figure,

$\Rightarrow \Delta ADB\sim \Delta CAB$ [ by AA similarity]

We get

$\Rightarrow \dfrac{AD}{CA}=\dfrac{AB}{CB}$ 

$\Rightarrow \dfrac{AD}{4}=\dfrac{3}{5}$

$\Rightarrow AD=\dfrac{12}{5}cm$

Also, 

$\Rightarrow \dfrac{DB}{AB}=\dfrac{AB}{CB}$ 

$\Rightarrow \dfrac{DB}{3}=\dfrac{3}{5}$

$\Rightarrow DB=\dfrac{9}{5}cm$

From figure,

$CD=BC-DB$ 

$\Rightarrow CD=5-\dfrac{9}{5}$

$\Rightarrow CD=\dfrac{16}{5}cm$

Now, volume of double cone is given as

$\Rightarrow \dfrac{1}{3}\pi {{\left( \dfrac{12}{5} \right)}^{2}}\left( \dfrac{9}{5} \right)+\dfrac{1}{3}\pi {{\left( \dfrac{12}{5} \right)}^{2}}\left( \dfrac{16}{5} \right)$ 

$\Rightarrow \dfrac{1}{3}\times 3.14{{\left( \dfrac{12}{5} \right)}^{2}}\left( \dfrac{9}{5} \right)+\dfrac{1}{3}\times 3.14{{\left( \dfrac{12}{5} \right)}^{2}}\left( \dfrac{16}{5} \right)$

$\Rightarrow \dfrac{1}{3}\times 3.14{{\left( \dfrac{12}{5} \right)}^{2}}\left[ \dfrac{16+9}{5} \right]$

$\Rightarrow \dfrac{1}{3}\times 3.14\times \dfrac{144}{5}$

$\therefore Volume=30.14c{{m}^{3}}$

Surface area of double cone is given as

$\Rightarrow \pi \dfrac{12}{5}\times 3+\pi \dfrac{12}{5}\times 4$

$\Rightarrow \pi \dfrac{12}{5}\left( 3+4 \right)$

$\Rightarrow 3.14\times \dfrac{12}{5}\times 7$

$\therefore \text{surface area}=52.75c{{m}^{2}}$

16. A cistern, internally measuring $150cm\times 120cm\times 110cm$ has $129600c{{m}^{3}}$ of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being $22.5cm\times 7.5cm\times 6.5cm$?

Ans: Given, volume of water is $129600c{{m}^{3}}$.

Volume of cistern is $150\times 120\times 110=1980000c{{m}^{3}}$

Now, volume of cistern to be filled is $1980000-129600=1850400c{{m}^{3}}$ 

Given the dimensions of a brick $22.5cm\times 7.5cm\times 6.5cm$.

Volume of a brick is $22.5\times 7.5\times 6.5=1096.875c{{m}^{3}}$

Let $n$ bricks absorbed water.

Water absorbed by $n$ bricks is $n\times \dfrac{1096.875}{17}c{{m}^{3}}$ 

$\Rightarrow n=\dfrac{1850400\times 17}{16\times 1096.875}$ 

$\therefore n=1792$

Therefore, $1792$ bricks absorbed the water.

17. In one fortnight of a given month, there was a rainfall of $10$ cm in a river valley. If the area of the valley is $97280k{{m}^{2}}$, show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each $1072km$ long, $75m$ wide and $3m$ deep.

Ans: Given the area of valley is $97280k{{m}^{2}}$.

Volume of rainfall is $97280\times \dfrac{10}{100\times 1000}$ 

Volume of rainfall is $9.728k{{m}^{3}}$.

Volume of three rivers is $3\times 1072\times \dfrac{75}{1000}\times \dfrac{3}{1000}$ 

So the volume of three rivers is $0.7236k{{m}^{3}}$.

Thus, $9.728k{{m}^{3}}=0.7236k{{m}^{3}}$

Therefore, the two are not approximately equivalent.

18. An oil funnel made of the tin sheet consists of a $10$ cm long cylindrical portion attached to a frustum of a cone. If the total height is $22$ cm, the diameter of the cylindrical portion is $8$ cm and the diameter of the top of the funnel is $18$ cm, find the area of the tin sheet required to make the funnel.

Ans: Slant height of the frustum of the cone is $l=\sqrt{{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}+{{h}^{2}}}$.

We get,

$\Rightarrow l=\sqrt{{{\left( 22-10 \right)}^{2}}+{{\left( \dfrac{18}{2}-\dfrac{8}{2} \right)}^{2}}}$

$\Rightarrow l=\sqrt{{{12}^{2}}+{{5}^{2}}}$

$\Rightarrow l=\sqrt{169}$

$\Rightarrow l=13cm$

Then, area of tin sheet is equal to the sum of curved surface area of cylinder and frustum.

We get

$\Rightarrow 2\pi \left( 4 \right)\left( 10 \right)+\pi \left( 4+9 \right)13$ 

$\Rightarrow 80\pi +169\pi $ 

$\Rightarrow 249\pi $

$\Rightarrow 249\times \dfrac{22}{7}$

$\Rightarrow 782\dfrac{4}{7}c{{m}^{2}}$

Therefore, area of tin shade is $782\dfrac{4}{7}c{{m}^{2}}$.

19. Determine the ratio of the volume of a cube to that of a sphere that exactly fit inside the cube.

Ans: Let the radius of the sphere which fits exactly into a cube be $r$ units. Then the length of each edge of a cube is $2r$ units.

Let ${{V}_{1}}$ and ${{V}_{2}}$ be the volumes of the cube and sphere

Then,

$\Rightarrow {{V}_{1}}={{\left( 2r \right)}^{3}}$ 

$\Rightarrow {{V}_{2}}=\dfrac{4}{3}\pi {{r}^{3}}$ 

Then,

$\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{8{{r}^{3}}}{\dfrac{4}{3}\pi {{r}^{3}}}$

$\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{6}{\pi }$

Therefore, the ratio of volume of cube to that of sphere is ${{V}_{1}}:{{V}_{2}}=6:\pi $. 

20. Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius $r$.

Ans: As cone is carved from a hemisphere 

So, the radius of the cone is equal to the radius of the hemisphere.

Also, the height of the cone is equal to the radius of the hemisphere.

So, volume of cone $=\dfrac{1}{3}\pi {{r}^{2}}\times r$ 

Therefore, volume of cone is $\dfrac{1}{3}\pi {{r}^{3}}$.

21. The height of a right circular cone is $12$ cm and the radius of its base is $4.5$ cm. Find its slant height.

Ans: We know that slant height of cone is $l=\sqrt{{{r}^{2}}+{{h}^{2}}}$ 

Given, $r=4.5cm$ and $h=12cm$ 

Substitute values, we get

$\Rightarrow l=\sqrt{{{\left( 4.5 \right)}^{2}}+{{12}^{2}}}$ 

$\Rightarrow l=\sqrt{20.25+144}$

$\Rightarrow l=\sqrt{164.25}$

$\Rightarrow l=12.816\text{ }approx$

Therefore, the slant height is approximately $12.816$cm.

22. How many balls, each of radius $1$ cm, can be made from a solid sphere of lead of radius $8$ cm.

Ans: We know that 

$\Rightarrow \text{Number of balls}=\dfrac{\text{Volume of sphere of radius 8 cm}}{\text{Volume of sphere of radius 1 cm}}$

$\Rightarrow \text{Number of balls}=\dfrac{\dfrac{4}{3}\pi {{\left( 8 \right)}^{3}}}{\dfrac{4}{3}\pi {{\left( 1 \right)}^{3}}}$

$\therefore \text{Number of balls}=512$

Therefore, 512 balls can be made.

23. A drinking glass is in the shape of a frustum of a cone of height $14$ cm. The diameter of its two circular ends is $4$ cm and $2$ cm. Find the capacity of the glass. $\left( \pi =\dfrac{22}{7} \right)$.

Ans: Given the diameter of two ends of a frustum cone are $4$ cm and $2$ cm.

So the radiuses are

${{r}_{1}}=1cm$ and ${{r}_{2}}=2cm$ 

Height $=14cm$ 

Now, capacity of glass is

\[\Rightarrow \dfrac{\pi h}{3}\left[ r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right]\] 

\[\Rightarrow \dfrac{22}{7}\times \dfrac{14}{3}\left[ {{1}^{2}}+{{2}^{2}}+2 \right]\]

\[\Rightarrow \dfrac{44}{3}\left[ 1+4+2 \right]\]

\[\Rightarrow \dfrac{44}{3}\times 7\]

\[\Rightarrow \dfrac{308}{3}\] 

\[\therefore \text{Capacity of glass}=102\dfrac{2}{3}\]

24. The diameter of a sphere is $6$ cm. It is melted and drawn into a wire of diameter $2$ cm. What is the length of the wire?

Ans: Given the diameter of a sphere is $6$ cm.

So, radius of sphere $r=\dfrac{6}{2}=3cm$ 

We know that volume of sphere is $\dfrac{4}{3}\pi {{r}^{3}}$.

Substitute values, we get

$\Rightarrow Volume=\dfrac{4}{3}\pi {{\left( 3 \right)}^{3}}$ 

$\Rightarrow Volume=36\pi \text{ }c{{m}^{3}}$

Let length of the wire is $l\text{ cm}$ 

Given the diameter of wire is $2cm$ 

So, radius of the wire $R=1cm$ 

Now, Volume of wire $=\pi {{R}^{2}}h$ 

$\Rightarrow Volume=\pi {{\left( 0.1 \right)}^{2}}\times l$ 

$\Rightarrow 36\pi =\pi \times l$

$\therefore l=3600 cm$

Therefore, length of wire is $36m$.

25. An iron pipe $20$ cm long has an exterior diameter equal to $25$ cm. If the thickness of the pipe is $1$ cm. Find the whole surface area of the pipe.

Ans: Given exterior diameter of a pipe is $25$ cm.

So exterior radius is $R=\dfrac{25}{2}=12.5cm$ 

Interior radius is $r=12.5-1=11.5cm$ 

Height $h=20cm$ 

So,

Total surface area of pipe is

\[\Rightarrow 2\pi \left( R+r \right)\left( h+R-r \right)\] 

Substitute values, we get

\[\Rightarrow 2\times \dfrac{22}{7}\left( 12.5+11.5 \right)\left( 20+12.5-11.5 \right)\]

\[\Rightarrow 2\times \dfrac{22}{7}\times 24\times 21\]

$\therefore \text{Total surface area}=3168c{{m}^{2}}$ 

Therefore, whole surface area of pipe is $3168c{{m}^{2}}$.

26. Find the ratio of the volumes of two circular cones. If ${{r}_{1}}:{{r}_{2}}=3:5$ and ${{h}_{1}}:{{h}_{2}}=2:1$. 

Ans: Ratio of volumes of two cones is given by

$\Rightarrow \dfrac{\dfrac{1}{3}\pi r_{1}^{2}{{h}_{1}}}{\dfrac{1}{3}\pi r_{2}^{2}{{h}_{2}}}$ 

\[\Rightarrow {{\left( \dfrac{{{r}_{1}}}{{{r}_{1}}} \right)}^{2}}\times \dfrac{{{h}_{1}}}{{{h}_{2}}}\]

Substituting values, we get

\[\Rightarrow {{\left( \dfrac{3}{5} \right)}^{2}}\times \dfrac{2}{1}\]

\[\Rightarrow \dfrac{9}{25}\times \dfrac{2}{1}\]

\[\Rightarrow \dfrac{18}{25}\]

Therefore, the ratio of volumes of two circular cones is $18:25$.  

27. A solid iron pole consists of a cylinder of height $110$ cm and of base diameter $24$ cm which is surmounted by a cone $9$ cm high, find the mass of the pole. Given that $1c{{m}^{3}}$ of iron has $8g$ mass approx. $\left[ \pi =\dfrac{355}{113} \right]$. 

Ans: For cylinder radius $r=\dfrac{12}{2}=6cm$ and height $h=110cm$ 

For cone radius $r=\dfrac{12}{2}=6cm$ and height $h=9cm$

\[\therefore Volume\text{ }of\text{ }pipe=volume\text{ }of\text{ }cylindrical\text{ }portion+volume\text{ }of\text{ }cone\] 

We get,

$\Rightarrow \pi {{r}^{2}}h+\dfrac{\pi {{r}^{2}}h}{3}$ 

\[\Rightarrow \pi {{\left( 6 \right)}^{2}}\times 110+\dfrac{\pi {{\left( 6 \right)}^{2}}\times 9}{3}\]

\[\Rightarrow 36\pi \left( 110+3 \right)\]

\[\Rightarrow 36\times \dfrac{355}{113}\times 113\]

\[\Rightarrow 36\times 355\]

\[\therefore \text{volume of pipe}=12780c{{m}^{3}}\]

Given that $1c{{m}^{3}}$ of iron has $8g$ mass approx.

Mass of \[12780c{{m}^{3}}\] iron is \[12780\times 8=102240gm\] 

Therefore, mass of pole is \[102240gm\].

28. $2$ cubes each of volume $64c{{m}^{3}}$ are joined end to end. Find the surface area of the resulting cuboid.

Ans: Abbreviation: CSA = Curved Surface Area TSA = Total Surface Area

V = Volume

We know that the volume of cube is given by ${{\left( side \right)}^{3}}$ 

Now, as given in the question, ${{\left( side \right)}^{3}}=64$

We can write

$\Rightarrow {{\left( side \right)}^{3}}={{4}^{3}}$

$\Rightarrow side=4cm$

So, for the resulting cuboid,

$length\left( l \right)=4+4=8cm$ 

$breadth\left( b \right)=4cm$

$height\left( h \right)=4cm$

Now, surface area of resulting cuboid $=2\left( lb+bh+hl \right)$ 

Substituting values, we get

$\Rightarrow \text{surface area }=2\left( 8\times 4+4\times 4+4\times 8 \right)$ 

$\Rightarrow \text{surface area }=2\left( 32+16+32 \right)$

$\Rightarrow \text{surface area }=2\times 80$

$\therefore \text{surface area }=160c{{m}^{2}}$

Therefore, surface area of resultant cuboid is $160c{{m}^{2}}$. 

29. Kuldeep made a birdbath for his garden in the shape of a cylinder with a hemispherical depression at one end. The height of the cylinder is $1.45$ cm and its radius is $30$ cm. Find the total surface area of the bird-bath. $\left( \pi =\dfrac{22}{7} \right)$.

Ans: Let $h$ be the height of cylinder and $r$ be the common radius of the cylinder and hemisphere.

We know that \[Total\text{ }surface\text{ }area\text{ }of\text{ }bird\text{ }bath=C.S.A.\text{ }of\text{ }cylinder+C.S.A.\text{ }of\text{ }hemisphere\] 

Substituting values, we get

$\Rightarrow 2\pi rh+2\pi {{r}^{2}}$ 

$\Rightarrow 2\pi r\left( r+h \right)$

$\Rightarrow 2\times \dfrac{22}{7}\times 30\left( 145+30 \right)c{{m}^{2}}$

$\Rightarrow 33000c{{m}^{2}}$

$\therefore \text{Total surface area}=3.3{{m}^{2}}$

30. A vessel is in the form of an inverted cone. Its height is $8$ cm and the radius of its top, which is open, is $5$ cm it is filled with water up to the brim. When lead shots each of which is a sphere of radius $0.5$ cm, are dropped into the vessel. One-fourth of the water flows out. Find the number of lead shots dropped.

Ans: Given, radius of lead shot $=0.5cm$ 

Radius of cone $=5cm$

Let $x$ be numbers of lead shots dropped.

$\therefore x\times \text{volume of one lead shot}=\dfrac{1}{4}\times \text{volume of cone}$ 

$\Rightarrow x\times \dfrac{4}{3}\pi {{\left( 0.5 \right)}^{3}}=\dfrac{1}{4}\times \dfrac{1}{3}\pi {{\left( 5 \right)}^{2}}\times 8$

$\Rightarrow x=\dfrac{25\times 8}{16{{\left( 0.5 \right)}^{3}}}$

$\therefore x=100$

Therefore, $100$ lead shots are dropped.

31. A cone of height $24$ cm and radius of base $6$ cm is made up of modelling clay. Find the volume of the cone.

Ans: Given,

Height of cone $h=24cm$ 

Radius of cone $r=6cm$ 

We know that volume of cone is $\dfrac{1}{3}\pi {{r}^{2}}h$.

$\Rightarrow Volume=\dfrac{1}{3}\pi {{\left( 6 \right)}^{2}}\times 24$ 

$\Rightarrow Volume=\dfrac{1}{3}\pi \times 36\times 24$

$\Rightarrow Volume=288\pi \text{ }c{{m}^{3}}$

Therefore, the volume of cone is $288\pi \text{ }c{{m}^{3}}$.

32. $2$ cubes each of volume $216c{{m}^{3}}$ are joined end to end. Find the surface area of the resulting cuboid.

Ans: Abbreviation: CSA = Curved Surface Area TSA = Total Surface Area

V = Volume

We know that the volume of cube is given by ${{\left( side \right)}^{3}}$ 

Now, as given in the question, ${{\left( side \right)}^{3}}=216$

We can write

$\Rightarrow {{\left( side \right)}^{3}}={{6}^{3}}$

$\Rightarrow side=6cm$

So, for the resulting cuboid,

$length\left( l \right)=6+6=12cm$ 

$breadth\left( b \right)=6cm$

$height\left( h \right)=6cm$

Now, surface area of resulting cuboid $=2\left( lb+bh+hl \right)$ 

Substituting values, we get

$\Rightarrow \text{surface area }=2\left( 12\times 6+6\times 6+6\times 12 \right)$ 

$\Rightarrow \text{surface area }=2\left( 72+36+72 \right)$

$\Rightarrow \text{surface area }=2\times 180$

$\therefore \text{surface area }=360c{{m}^{2}}$

Therefore, surface area of resulting cuboid is $360c{{m}^{2}}$.

33. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is $14$ cm and the total height of the Vessel is $13$ cm. Find inner surface area.

Ans: We know that inner surface area $=2\pi rh+2\pi {{r}^{2}}$ 

Radius of base of the cylinder is equal to the radius of hemisphere.

We get,

\[\Rightarrow Inner\text{ }surface\text{ }area~=2\pi r\left( r+h \right)\] 

\[\Rightarrow Inner\text{ }surface\text{ }area~=2\times \dfrac{22}{7}\times 7\left( 6+7 \right)\]

\[\Rightarrow Inner\text{ }surface\text{ }area~=44\times 13\]

\[\Rightarrow Inner\text{ }surface\text{ }area~=572c{{m}^{2}}\]

Therefore, inner surface area is $572c{{m}^{2}}$. 

34. A spherical ball of diameter $21$ cm is melted and recast into cubes each of side $1$ cm. Find the number of cubes thus formed. $\left( \pi =\dfrac{22}{7} \right)$. 

Ans: We know that volume of spherical ball $=\dfrac{4}{3}\pi {{r}^{3}}$

We get,

$\Rightarrow Volume=\dfrac{4}{3}\pi \times \dfrac{1}{21}\times \dfrac{1}{21}\times \dfrac{1}{21}c{{m}^{3}}$ 

Given each side of cube is $1$ cm.

Then, volume of each cube $=1\times 1\times 1c{{m}^{3}}$ 

$\therefore \text{Number of cubes}=\dfrac{\text{Volume of ball}}{\text{Volume of cube}}$ 

Substituting values, we get

$\Rightarrow \text{Number of cubes}=\dfrac{\dfrac{4}{3}\times \dfrac{22}{7}\times \dfrac{1}{21}\times \dfrac{1}{21}\times \dfrac{1}{21}c{{m}^{3}}}{1}$

$\therefore \text{Number of cubes}=4851$

Therefore, the number of cubes formed are $4851$.

3 Marks Questions

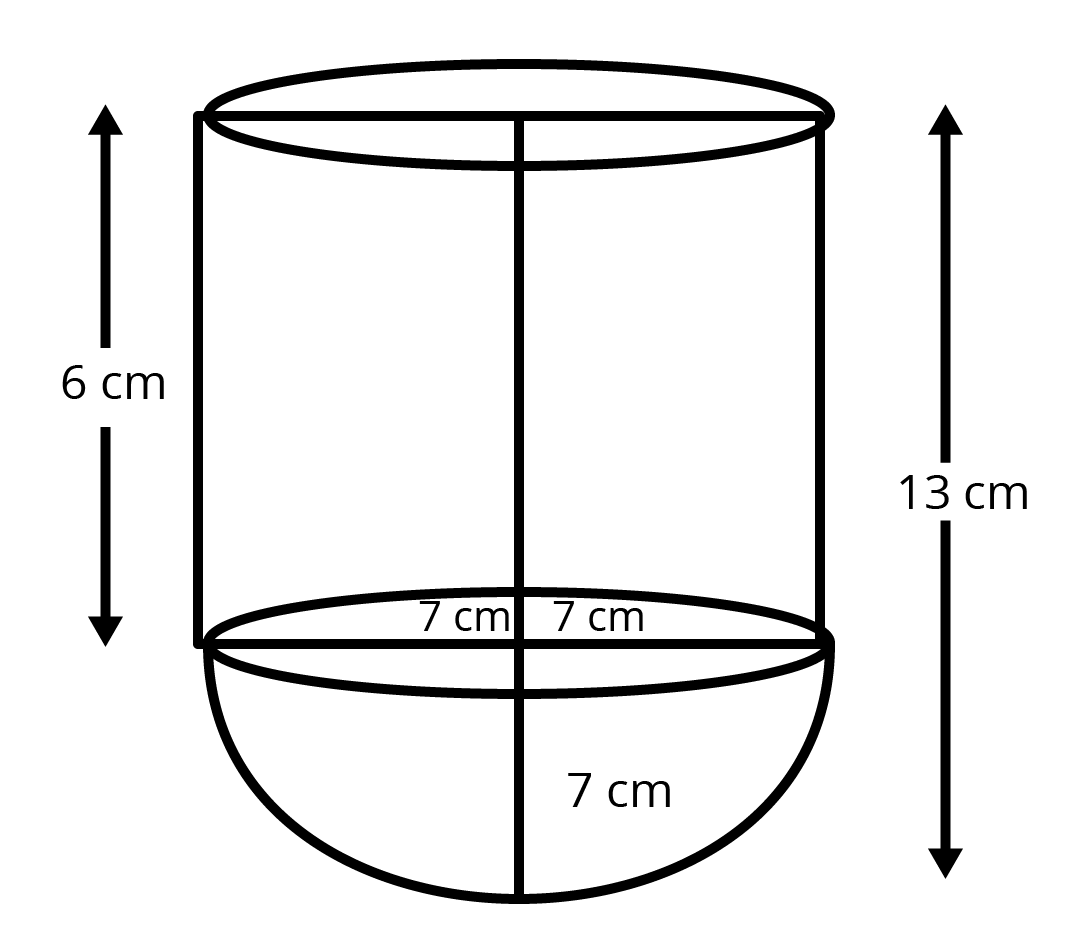
1. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is $14$ cm and the total height of the Vessel is $13$ cm. Find the inner surface area of the vessel.

Ans: Given, the diameter of hemisphere is $14$ cm.

So, the radius of hemisphere is $r=\dfrac{14}{2}=7cm$ 

Height of vessel is $13$ cm and height of hollow cylinder will be $13-7=6cm$ 

We know that inner surface area $=2\pi rh+2\pi {{r}^{2}}$ 

Radius of base of the cylinder is equal to the radius of hemisphere.

We get,

\[\Rightarrow Inner\text{ }surface\text{ }area~=2\pi r\left( r+h \right)\] 

\[\Rightarrow Inner\text{ }surface\text{ }area~=2\times \dfrac{22}{7}\times 7\left( 6+7 \right)\]

\[\Rightarrow Inner\text{ }surface\text{ }area~=44\times 13\]

\[\Rightarrow Inner\text{ }surface\text{ }area~=572c{{m}^{2}}\]

Therefore, inner surface area is $572c{{m}^{2}}$. 

2. A toy is in the form of a cone of radius $3.5$ cm mounted on a hemisphere of the same radius. The total height of the toy is $15.5$ cm. Find the total surface area of the toy.

Ans: Given the radius of a cone is $3.5$cm.

The radius of the hemisphere and cone are the same, so the radius of the hemisphere is $3.5$cm.

Total height of the toy is $15.5$ cm.

The height of the cone will be $15.5-3.5=12cm$ 

Slant height of the cone $l=\sqrt{{{r}^{2}}+{{h}^{2}}}$

$\Rightarrow l=\sqrt{{{\left( 3.5 \right)}^{2}}+{{12}^{2}}}$

$\Rightarrow l=\sqrt{12.25+144}$

$\Rightarrow l=\sqrt{156.25}$

$\Rightarrow l=12.5cm$

Now, the total surface area of the toy is equal to the sum of the curved surface area of the hemisphere and the curved surface area of the cone.

We get

$\Rightarrow TSA=2\pi {{r}^{2}}+\pi rl$ 

$\Rightarrow TSA=2\pi {{\left( 3.5 \right)}^{2}}+\pi \left( 3.5 \right)\left( 12.5 \right)$

$\Rightarrow TSA=24.5\pi +43.75\pi $

$\Rightarrow TSA=68.25\pi $

$\Rightarrow TSA=68.25\times \dfrac{22}{7}$

$\therefore TSA=214.5c{{m}^{2}}$

Therefore, total surface area of toy is $214.5c{{m}^{2}}$.

3. A cubical block of side $7$ cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.

Ans: Given the side of the cubical block is $7cm$.

The greatest diameter of the hemisphere will be $7cm$.

The total surface area of solid will be equal to the sum of the external surface area of the cubical block and curved surface area of the hemisphere.

We get

$\Rightarrow TSA=\left\{ 6{{\left( 7 \right)}^{2}}+\pi {{\left( \dfrac{7}{2} \right)}^{2}} \right\}+2\pi {{\left( \dfrac{7}{2} \right)}^{2}}$ 

$\Rightarrow TSA=\left\{ 294+\dfrac{49}{4}\pi  \right\}+\dfrac{49}{4}\pi $

$\Rightarrow TSA=294+\dfrac{49}{4}\pi $

$\Rightarrow TSA=294+\dfrac{49}{4}\times \dfrac{22}{7}$

$\Rightarrow TSA=294+\dfrac{77}{2}$

$\Rightarrow TSA=294+38.5$

$\Rightarrow TSA=332.5c{{m}^{2}}$

Therefore, total surface area of solid is $332.5c{{m}^{2}}$.

4. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter $l$ of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid

Ans: Given that the diameter of hemisphere is equal to the edge of cube.

Diameter of hemisphere is $l$ so length of edge of the cube is $l$.

Surface area of remaining solid is

$\Rightarrow 2\pi {{\left( \dfrac{l}{2} \right)}^{2}}+6\times {{l}^{2}}-\pi {{\left( \dfrac{l}{2} \right)}^{2}}$ 

$\Rightarrow \pi {{\left( \dfrac{l}{2} \right)}^{2}}+6\times {{l}^{2}}$

$\Rightarrow \dfrac{1}{4}{{l}^{2}}\left( \pi +24 \right)$

Therefore, surface area of the remaining solid is $\dfrac{1}{4}{{l}^{2}}\left( \pi +24 \right)$.

5. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is $3$ cm and its length is $12$ cm. If each cone has a height of $2$ cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)

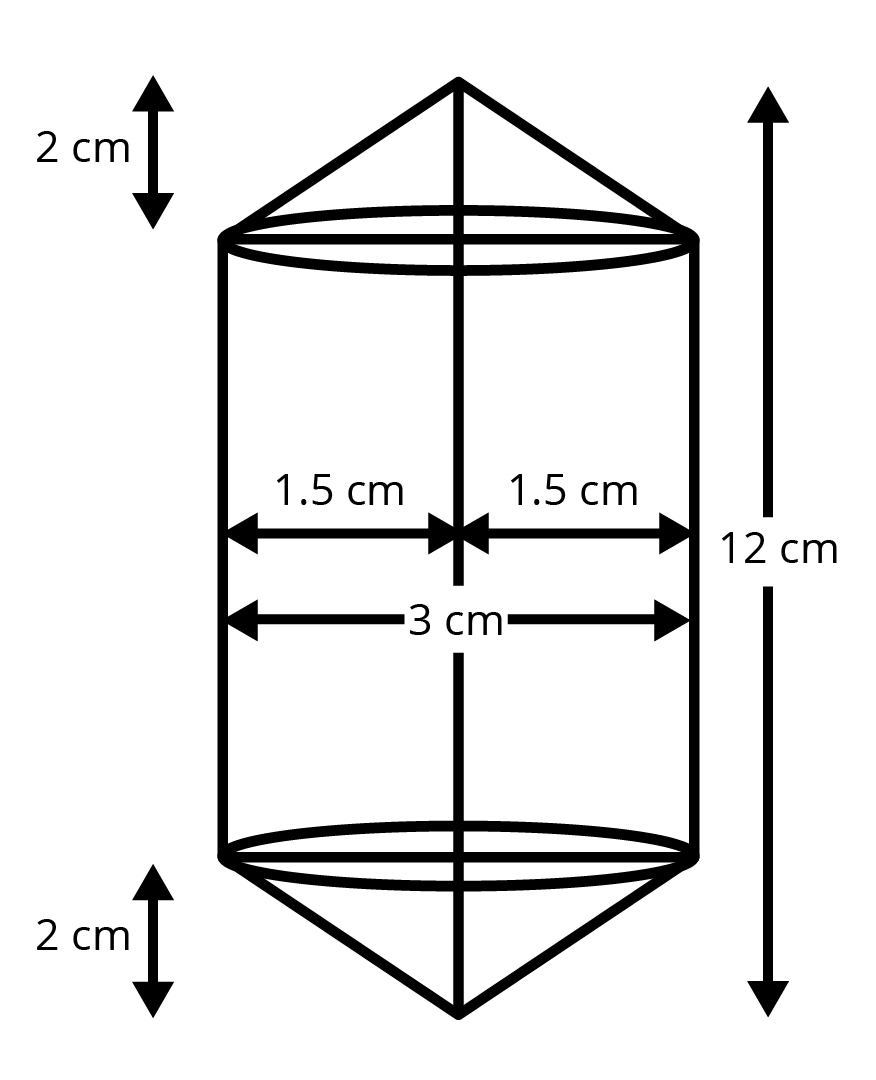
Ans: For upper conical portion, radius of the base is $1.5cm$ and height $=2cm$  

Then, volume is $\dfrac{1}{3}\pi {{r}^{2}}h=\dfrac{1}{3}\pi {{\left( 1.5 \right)}^{2}}\times 2=1.5\pi \text{ }c{{m}^{3}}$ 

Similarly for lower portion, radius of the base is $1.5cm$ and height $=2cm$  

Then, volume is $\dfrac{1}{3}\pi {{r}^{2}}h=\dfrac{1}{3}\pi {{\left( 1.5 \right)}^{2}}\times 2=1.5\pi \text{ }c{{m}^{3}}$

For middle portion radius of the base is $1.5cm$ and height $=12-2-2=8cm$

Then, volume of middle portion is $\pi {{r}^{2}}h=\pi {{\left( 1.5 \right)}^{2}}\times 8=18\pi \text{ }c{{m}^{3}}$

Now, volume of model is 

$\Rightarrow V=1.5\pi +1.5\pi +18\pi $

$\Rightarrow V=21\pi $ 

$\Rightarrow V=21\times \dfrac{22}{7}$

$\Rightarrow V=66c{{m}^{3}}$

Therefore, volume of model is $66c{{m}^{3}}$.

6. A Gulab Jamun contains sugar syrup up to about $30%$ of its volume. Find approximately how much syrup would be found in $45$ Gulab Jamun, each shaped like a cylinder with two hemispherical ends, with length $5$ cm and diameter $2.8$ cm (see figure).

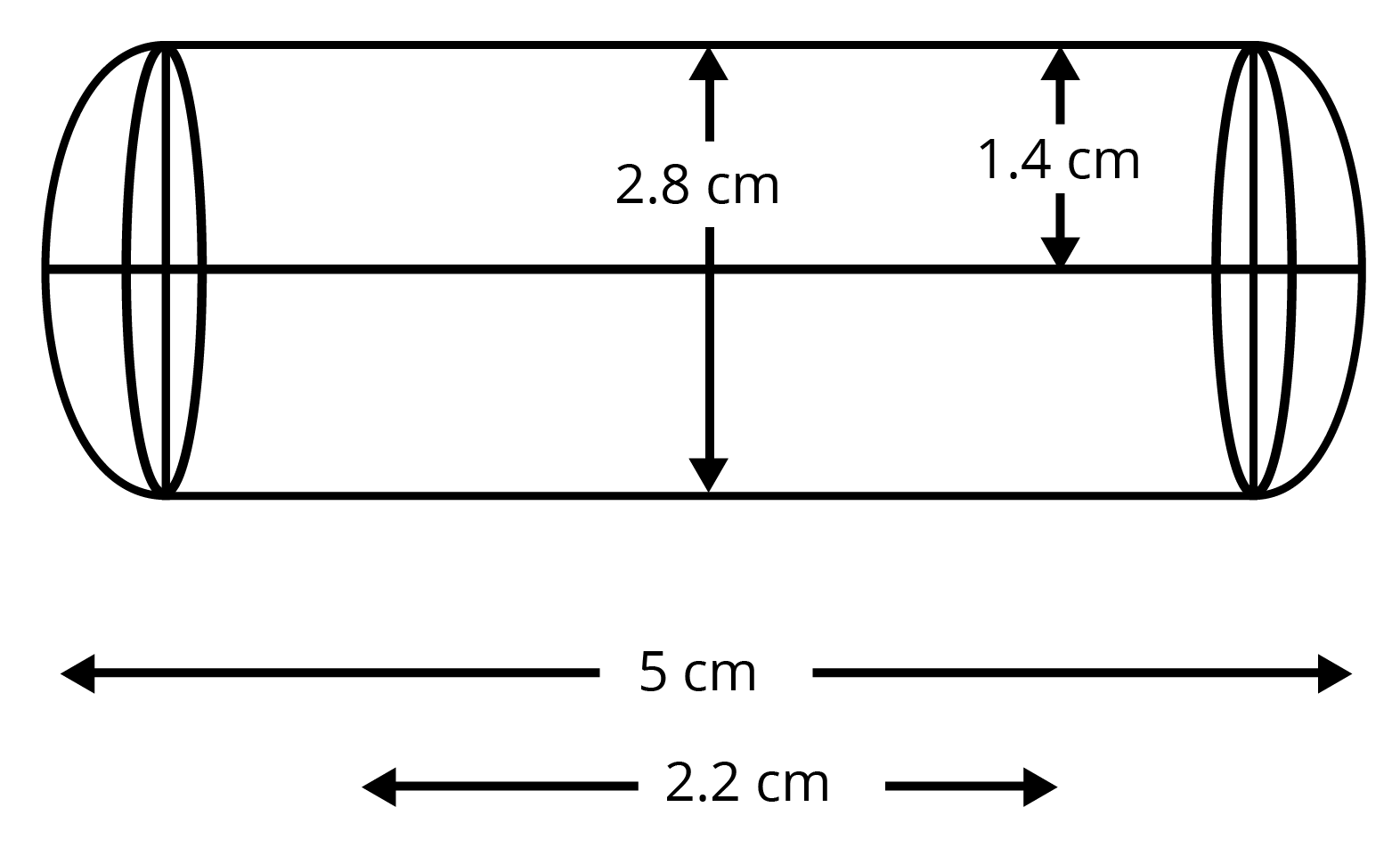
Ans: Given the diameter of gulabjamun is $2.8$ cm and height $5$ cm.

Volume of gulabjamun is equal to the sum of volumes of two hemispherical ends and a cylinder.

We get

$\Rightarrow V=\dfrac{2}{3}\pi {{r}^{3}}+\pi {{r}^{2}}h+\dfrac{2}{3}\pi {{r}^{3}}$

$\Rightarrow V=\dfrac{2}{3}\pi {{\left( 1.4 \right)}^{3}}+\pi {{\left( 1.4 \right)}^{2}}2.2+\dfrac{2}{3}\pi {{\left( 1.4 \right)}^{3}}$

$\Rightarrow V=\dfrac{4}{3}\pi {{\left( 1.4 \right)}^{3}}+\pi {{\left( 1.4 \right)}^{2}}2.2$

$\Rightarrow V=\pi {{\left( 1.4 \right)}^{2}}\left[ \dfrac{4\times 1.4}{3}+2.2 \right]$

$\Rightarrow V=\pi {{\left( 1.4 \right)}^{2}}\left[ \dfrac{5.6+6.6}{3} \right]$

$\Rightarrow V=\dfrac{1.96\times 12.2}{3}\pi \text{ c}{{\text{m}}^{3}}$

Now, volume of $45$ gulabjamuns will be

$\Rightarrow V=45\times \dfrac{1.96\times 12.2}{3}\pi \text{ c}{{\text{m}}^{3}}$

$\Rightarrow V=15\times 1.96\times 12.2\times \dfrac{22}{7}\text{ c}{{\text{m}}^{3}}$

$\therefore V=1127.28\text{ c}{{\text{m}}^{3}}$

Since gulabjamun contains $30%$ sugar syrup

So volume of sugar syrup is $\dfrac{30}{100}\times 1127.28=338.184\text{ c}{{\text{m}}^{3}}$

Therefore, volume of sugar syrup is $338\text{c}{{\text{m}}^{3}}$ (approx.).

7. A vessel is in the form of an inverted cone. Its height is $8$ cm and the radius of its top, which is open, is $5$ cm it is filled with water up to the brim. When lead shots each of which is a sphere of radius $0.5$ cm, are dropped into the vessel. One-fourth of the water flows out. Find the number of lead shots dropped.

Ans: Given, radius of lead shot $=0.5cm$ 

Radius of cone $=5cm$

Let $x$ be numbers of lead shots dropped.

$\therefore x\times \text{volume of one lead shot}=\dfrac{1}{4}\times \text{volume of cone}$ 

$\Rightarrow x\times \dfrac{4}{3}\pi {{\left( 0.5 \right)}^{3}}=\dfrac{1}{4}\times \dfrac{1}{3}\pi {{\left( 5 \right)}^{2}}\times 8$

$\Rightarrow x=\dfrac{25\times 8}{16{{\left( 0.5 \right)}^{3}}}$

$\therefore x=100$

Therefore, $100$ lead shots are dropped.

8. A solid iron pole consists of a cylinder of height $220$ cm and of base diameter $24$ cm which is surrounded by another cylinder of height $60$ cm and radius $8cm$. Find the mass of the pole, given that $1c{{m}^{3}}$ of iron has $8g$ mass approx. $\left[ \pi =3.14 \right]$. 

Ans: For lower cylinder radius $r=\dfrac{24}{2}=12cm$ and height $h=220cm$ 

For upper cylinder radius $R=8cm$ and height $H=60cm$

\[\therefore Volume\text{ }of\text{ pole}=volume\text{ }of\text{ lower }cylinder+volume\text{ }of\text{ upper }cylinder\] 

We get,

$\Rightarrow \pi {{r}^{2}}h+\pi {{R}^{2}}H$ 

\[\Rightarrow \pi {{\left( 12 \right)}^{2}}\times 220+\pi {{\left( 8 \right)}^{2}}\times 60\]

\[\Rightarrow \pi \left( 31680+3840 \right)\]

\[\Rightarrow 35520\times 3.14\]

\[\therefore \text{volume of pipe}=111532.8c{{m}^{3}}\]

Given that $1c{{m}^{3}}$ of iron has $8g$ mass approx.

Mass of \[111532.8c{{m}^{3}}\] iron is \[11532.8\times 8=92262.4gm\] 

Therefore, mass of pole is \[92262.4gm\].

9. A solid consisting of a right circular cone of height $120cm$ and radius $60cm$ standing on a hemisphere of radius $60cm$ is placed upright in a right circular cylinder, full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is $60cm$ and its height is $180cm$. 

Ans: Given, the radius of the cylinder is $60cm$ and its height is $180cm$.

Volume of cylinder is $\pi {{\left( 60 \right)}^{2}}\times 180=648000\pi \text{ c}{{\text{m}}^{3}}$ 

Given, the radius of the hemisphere is $60cm$.

Volume of hemisphere is $\dfrac{2}{3}\pi {{\left( 60 \right)}^{3}}=144000\pi \text{ c}{{\text{m}}^{3}}$ 

Volume of cone is $\dfrac{1}{3}\pi {{\left( 60 \right)}^{2}}\times 120=144000\pi \text{ c}{{\text{m}}^{3}}$ 

Volume of water left in the cylinder is

$\Rightarrow 648000\pi -144000\pi -144000\pi $ 

$\Rightarrow 360000\pi $

$\Rightarrow \dfrac{360000}{100\times 100\times 100}\pi {{m}^{3}}$

$\Rightarrow 0.36\times \dfrac{22}{7}{{m}^{3}}$

$\Rightarrow 1.131{{m}^{3}}$

Therefore, volume of water left is approximately $1.131{{m}^{3}}$.

10. A spherical glass vessel has a cylindrical neck $8$ cm long, $2$ m in diameter, the diameter of the spherical part is $8.5$ cm. by measuring the amount of water it holds, a child finds its volume to be $345c{{m}^{3}}$, check whether she is correct, taking the above as side measurements. $\left[ \pi =3.14 \right]$. 

Ans: Given that a spherical glass vessel has a cylindrical neck $8$ cm long, $2$ m in diameter, and the diameter of the spherical part is $8.5$ cm.

Now, radius of cylindrical part is $r=1cm$ and height $h=8cm$ 

Radius of spherical part is $R=\dfrac{8.5}{2}=\dfrac{17}{4}cm$ 

Now, volume of glass solid is equal to the sum of volume of cylindrical part and volume of spherical part.

We get

$\Rightarrow Volume=\pi {{r}^{2}}h+\dfrac{4}{3}\pi {{R}^{3}}$ 

$\Rightarrow Volume=3.14\times {{\left( 1 \right)}^{2}}\times 8+\dfrac{4}{3}\times 3.14\times {{\left( \dfrac{17}{4} \right)}^{3}}$

$\Rightarrow Volume=3.14\left[ 8+\dfrac{4913}{48} \right]$

$\Rightarrow Volume=3.14\left[ \dfrac{384+4913}{48} \right]$

$\Rightarrow Volume=3.14\times \dfrac{5297}{48}$

$\Rightarrow Volume=3.14\times \dfrac{5297}{48}$

$\therefore Volume=346.51c{{m}^{3}}$

Therefore, the volume finds by the student is not correct.

11. A cylindrical bucket, $32$ cm and high and with a radius of base $18$ cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is $24$ cm, find the radius and slant height of the heap.

Ans: For cylindrical bucket, Radius of the base $r=18cm$  and height $h=32cm$ 

Volume of bucket is $\pi {{r}^{2}}h=\pi {{\left( 18 \right)}^{2}}32=10368\pi \text{ c}{{\text{m}}^{3}}$ 

Height of conical heap is $24cm$ 

Let the radius of heap is ${{r}_{1}}$ 

Then volume of conical heap is

$\Rightarrow \dfrac{1}{3}\pi {{r}_{1}}^{2}\times 24=8\pi {{r}_{1}}^{2}\text{ c}{{\text{m}}^{3}}$ 

Now, bucket is emptied on the ground and conical heap is formed.

So the volumes of bucket and conical heap are equal.

We get

$\Rightarrow 10368\pi =8\pi {{r}_{1}}^{2}$

$\Rightarrow {{r}_{1}}^{2}=\dfrac{10368\pi }{8\pi }$

$\Rightarrow {{r}_{1}}^{2}=1296$

$\therefore {{r}_{1}}=36cm$

Now, slant height of heap is

$\Rightarrow l=\sqrt{{{36}^{2}}+{{24}^{2}}}$ 

$\Rightarrow l=\sqrt{1296+576}$

$\Rightarrow l=\sqrt{1872}$

$\therefore l=12\sqrt{13}cm$

Therefore, slant height of conical heap is $12\sqrt{13}cm$.

12. Water in a canal $6m$ wide and $1.5m$ deep is flowing with a velocity of $10km/h$. How much area will it irrigate in $30$ minutes if $8cm$ of standing water is needed?

Ans: Given the width of canal is $6m$ and

Depth of canal is $1.5m=\dfrac{3}{2}m$

Velocity of water is $10km/h=10000m/h$.

Length of water column formed in $30$ minutes is $10000\times \dfrac{1}{2}=5000m$ 

Volume of water flows in $30$ minutes is $6\times \dfrac{3}{2}\times 5000=45000{{m}^{3}}$

The area irrigated will be $\dfrac{45000}{\dfrac{8}{100}}=\dfrac{4500000}{8}=562500{{m}^{2}}$

Therefore, $562500{{m}^{2}}=56.25hectares$ area will be irrigated.

13. A farmer connects a pipe of internal diameter $20cm$ from a canal into a cylindrical tank in his field which is $10m$ in diameter and $2m$ deep. If water flows through the pipe at the rate of $3km/h$, in how much time will the tank be filled?

Ans: Given, rate of water flowing $=3km/hr=50m/\min $ 

So in one second $\dfrac{5}{6}m$ water flows

Internal diameter of pipe is $20cm$.

So radius is $10cm=0.1m$ 

So volume of water flows through the pipe in one second is

$\Rightarrow \pi {{r}^{2}}h$ 

$\Rightarrow \pi \times {{\left( 0.1 \right)}^{2}}\times 50$

$\Rightarrow \dfrac{\pi }{2}{{m}^{3}}$

Given the diameter of tank is $10m$ and height is $2m$. 

Volume of water in tank is

$\Rightarrow \pi {{r}^{2}}h$ 

$\Rightarrow \pi \times {{\left( \dfrac{10}{2} \right)}^{2}}\times 2$

$\Rightarrow 50\pi \text{ }{{m}^{3}}$

Time taken to fill the tank is $\dfrac{50\pi }{\dfrac{\pi }{2}}$ .

We get

\[\Rightarrow \dfrac{50\pi }{\dfrac{\pi }{2}}=100\text{minutes}\] 

Therefore, time taken to fill the tank is $\text{1 hour 40 minutes}$. 

14. A metallic circular cone $20cm$ height with a vertical angle of $60$ is cut into two parts at the middle point of its height by a plane parallel to the base. If the frustum, so obtained be drawn into a wire of diameter $\dfrac{1}{16}$ cm. Find the length of the wire.

Ans: Let ${{r}_{1}}$ and ${{r}_{2}}$ be the radii of lower and upper ends of a frustum cone.

We get

\[\Rightarrow \dfrac{{{r}_{1}}}{20}=\tan 30{}^\circ \] 

Then,

${{r}_{1}}=\dfrac{20}{\sqrt{3}}cm$ and ${{r}_{2}}=\dfrac{10}{\sqrt{3}}cm$ 

Height $=20cm$ 

Now, volume of frustum is

\[\Rightarrow \dfrac{1}{3}\pi \times 10\left[ {{\left( \dfrac{20}{\sqrt{3}} \right)}^{2}}+{{\left( \dfrac{10}{\sqrt{3}} \right)}^{2}}+\dfrac{20}{\sqrt{3}}\times \dfrac{10}{\sqrt{3}} \right]\] 

\[\Rightarrow \dfrac{1}{3}\pi \times 10\left[ \dfrac{400}{3}+\dfrac{100}{3}+\dfrac{200}{3} \right]\]

Since the frustum is drawn in to wire so the volumes of both are equal.

Let $l$ be the length of wire.

We get

\[\Rightarrow \dfrac{1}{3}\pi \times 10\left[ \dfrac{400}{3}+\dfrac{100}{3}+\dfrac{200}{3} \right]=\pi {{\left( \dfrac{1}{32} \right)}^{2}}\times l\]

\[\Rightarrow \dfrac{1}{3}\times 10\times \dfrac{700}{3}=\dfrac{1}{1024}\times l\]

\[\Rightarrow l=\dfrac{10\times 1024\times 700}{9}\]

\[\Rightarrow l=\dfrac{7168000}{9}\]

\[\therefore l=796444.4cm=7964.4m\]

Therefore, the length of wire is \[7964.4m\].

15. The diameter of a metallic sphere is $6$ cm. The sphere is melted and drawn into a wire of uniform cross-section. If the length of the wire is $36$ cm, find its radius.

Ans: Given the diameter of sphere is $6cm$ 

For sphere, Radius $r=3cm$ 

So, Volume$=\dfrac{4}{3}\pi {{r}^{3}}$ 

\[\Rightarrow Volume=\dfrac{4}{3}\pi {{\left( 3 \right)}^{3}}c{{m}^{3}}\] 

Let radius of wire be $R$.

Then, Volume of wire is $=\dfrac{4}{3}\pi {{R}^{3}}$ 

Sphere is melted and drawn into a wire so the volumes of both are equal.

So, we get

$\Rightarrow 36\pi =36\times \pi {{R}^{2}}$

$\Rightarrow {{R}^{2}}=\dfrac{1}{100}$

$\therefore R=0.1cm$

Therefore, the radius of wire is $0.1cm$.

16. Water flows at the rate of $10$ meter per minute through a cylindrical pipe having its diameter at $5$ mm. How much time will it take to fill a conical vessel where the diameter of the base is 40 cm and the depth is 24 cm?

Ans: Given, rate of water flowing $10m/\min $ 

The internal diameter of the pipe is $5mm$.

So radius is $\dfrac{5}{2}mm=\dfrac{1}{4}cm$  and height $h=1000cm$ 

So volume of cylinder is 

$\Rightarrow \pi {{r}^{2}}h$ 

$\Rightarrow \pi \times {{\left( \dfrac{1}{4} \right)}^{2}}\times 1000c{{m}^{3}}$

Given the diameter of conical vessel is $40m$ and height is $24m$. 

Let conical vessel is filled in $x\text{ minutes}$ 

Volume of conical vessel is

$\Rightarrow \dfrac{1}{3}\pi {{\left( 20 \right)}^{2}}24$ 

Now, volume of water flows is 

$\Rightarrow \pi {{r}^{2}}h\times x$ 

$\Rightarrow \pi \times {{\left( \dfrac{1}{4} \right)}^{2}}\times 100\times x=\dfrac{1}{3}\pi {{\left( 20 \right)}^{2}}24$

$\Rightarrow \dfrac{1}{16}\times 100\times x=\dfrac{1}{3}\times 400\times 24$

$\Rightarrow x=\dfrac{1}{3}\times \dfrac{400\times 24\times 16}{100}$

$\therefore x=\dfrac{512}{10}\text{minutes}$

Therefore, the time taken to fill the tank is $\text{51 minutes 12 seconds}$. 

17. The radius of the base and the height of solid right cylinder are in the ratio $2:3$ and its volume is $1617c{{m}^{3}}$. Find the total surface area of the cylinder. $\left( \pi =\dfrac{22}{7} \right)$.

Ans: Let $r$ be the radius of the base and $h$ be the height of the solid right circular cylinder.

Given the ratio of base and height is $2:3$.

We get

$\Rightarrow \dfrac{r}{h}=\dfrac{2}{3}$ 

$\Rightarrow r=\dfrac{2h}{3}$

Volume of the cylinder is $\pi {{r}^{2}}h$.

We get

$\Rightarrow \pi \times \dfrac{4}{9}{{h}^{2}}\times h=1617$ 

$\Rightarrow {{h}^{3}}=\dfrac{9}{4}\times \dfrac{1617}{22}\times 7$

$\Rightarrow {{h}^{3}}=\dfrac{101871}{88}$

$\Rightarrow h=\dfrac{21}{2}$

Surface area of cylinder is $2\pi rh+2\pi {{r}^{2}}$

We get

$\Rightarrow \text{Surface area}=2\pi \times \dfrac{2h}{3}\times h+\dfrac{8\pi {{h}^{2}}}{9}$ 

$\Rightarrow \text{Surface area}=\dfrac{\pi {{h}^{2}}}{9}\left[ 12+8 \right]$

$\Rightarrow \text{Surface area}=\dfrac{20\pi {{h}^{2}}}{9}$

$\Rightarrow \text{Surface area}=\dfrac{20\pi }{9}\times \dfrac{21}{2}\times \dfrac{21}{2}$

$\Rightarrow \text{Surface area}=5\times 22\times 7$

$\therefore \text{Surface area}=770c{{m}^{2}}$

Therefore, the total surface area of cylinder is $770c{{m}^{2}}$.

18. A toy is in the form of a cone mounted on a hemisphere of a common base radius of $7$ cm. The total height of the toy is $31$ cm. Find the total surface area of the toy.

Ans: Given the radius of a cone is $7$cm.

The radius of the hemisphere and cone are the same, so the radius of the hemisphere is $7$ cm.

The total height of the toy is $31$ cm.

The height of the cone will be $31-7=24cm$ 

Slant height of the cone $l=\sqrt{{{r}^{2}}+{{h}^{2}}}$

$\Rightarrow l=\sqrt{{{7}^{2}}+{{24}^{2}}}$

$\Rightarrow l=\sqrt{49+576}$

$\Rightarrow l=\sqrt{625}$

$\Rightarrow l=25cm$

Now, the total surface area of the toy is equal to the sum of the curved surface area of a hemisphere and the curved surface area of the cone.

We get

$\Rightarrow TSA=2\pi {{r}^{2}}+\pi rl$ 

$\Rightarrow TSA=2\pi {{\left( 7 \right)}^{2}}+\pi \left( 7 \right)\left( 25 \right)$

$\Rightarrow TSA=98\pi +175\pi $

$\Rightarrow TSA=273\pi $

$\Rightarrow TSA=273\times \dfrac{22}{7}$

$\therefore TSA=858c{{m}^{2}}$

Therefore, total surface area of toy is $858c{{m}^{2}}$.

19. A well $3.5$ m in diameter and $20$m deep be dug in a rectangular field $20$ m by $14$ m. The earth taken out is spread evenly on the field. Find the level of the earth raised in the field.

Ans: Given, Diameter of well $=3.5m$ 

So, the radius of well $r=\dfrac{7}{4}m$

And Depth of earth dug $h=20m$ 

Volume of earth taken out is $\pi {{r}^{2}}h$ 

We get

$\Rightarrow \dfrac{22}{7}\times \dfrac{7}{4}\times \dfrac{7}{4}\times 20=\dfrac{385}{2}{{m}^{3}}$ 

Given, the earth from digging is evenly spread out.

So, Length of platform $l=20m$, and Breadth of platform $b=14m$ 

Arear of field is $l\times b=20\times 14=280{{m}^{2}}$

Area of field excluding well is 

$\Rightarrow \left( 280-\dfrac{22}{7}\times \dfrac{7}{4}\times \dfrac{7}{4} \right)=\dfrac{2163}{8}{{m}^{2}}$

$\Rightarrow \text{Level of earth raised}=\dfrac{\text{Volume of earth taken out}}{\text{Area of field}}$ 

$\Rightarrow \text{Level of earth raised}=\dfrac{385}{2}\times \dfrac{8}{2163}$

$\therefore \text{Level of earth raised}=0.7119m$

Therefore, the level of earth raised in the field is $71.19cm$. 

20. A solid sphere of radius $6$ cm is melted into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is $5$ cm and its height is $32$ cm, find the uniform thickness of the cylinder.

Ans: Given the radius of solid sphere is $6cm$ 

So, the volume of sphere is given by

$\Rightarrow Volume=\dfrac{4}{3}\pi {{r}^{3}}$

$\Rightarrow Volume=\dfrac{4}{3}\pi {{\left( 6 \right)}^{3}}$

$\Rightarrow Volume=288\pi \text{ }c{{m}^{3}}$

Given the external radius of the base of the cylinder is $5cm$ and height is $32cm$. 

Let the internal radius of the cylinder be $x$ 

Volume of hollow cylinder and solid sphere must be equal.

We get

$\Rightarrow 32\left( {{5}^{2}}-{{x}^{2}} \right)\pi =288\pi $ 

$\Rightarrow 25-{{x}^{2}}=\dfrac{288}{32}$

$\Rightarrow 25-{{x}^{2}}=9$

$\Rightarrow {{x}^{2}}=25-9$

$\Rightarrow {{x}^{2}}=16$

$\Rightarrow x=4$

Therefore, the uniform thickness of the cylinder is $4cm$.

21. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see figure). The length of the entire capsule is $14mm$ and the diameter of the capsule is $5mm$. Find its surface area.

Ans: Given that the diameter of the capsule is $5mm$.

So the radius of the hemisphere is $r=2.5mm$ 

Height of cylinder is equal to the difference of total height to that of diameter of sphere.

We get

$\Rightarrow h=14-\left( 2.5+2.5 \right)=9mm$ 

Total surface area of the capsule is given by

$\Rightarrow 2\pi rh+2\left( 2\pi {{r}^{2}} \right)$ 

$\Rightarrow 2\pi \left( \dfrac{5}{2} \right)\left( 9 \right)+2\left( 2\pi {{\left( \dfrac{5}{2} \right)}^{2}} \right)$

$\Rightarrow 45\pi +25\pi $

$\Rightarrow 70\pi $

$\Rightarrow 70\times \dfrac{22}{7}$

$\Rightarrow \text{Surface area}=220m{{m}^{2}}$

Therefore, total surface area of capsule is $220m{{m}^{2}}$.

22. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are $15$ cm by $10$ cm by $3.5$ cm. The radius of each of the depressions is $0.5$ cm and the depth is $1.4$ cm. Find the volume of wood in the entire stand.

Ans: We know that volume of the cuboid $=l\times b\times h$ 

Given dimensions of the cuboid are $15cm\times 10cm\times 3.5cm$ 

So the volume of cuboid is

$\Rightarrow 15\times 10\times 3.5$ 

$\Rightarrow 525c{{m}^{3}}$

Now, volume of conical depression $=\dfrac{2}{3}\pi {{r}^{2}}h$

\[\Rightarrow Volume=\dfrac{2}{3}\times \dfrac{22}{7}\times 0.5\times 0.5\times 1.4\] 

\[\Rightarrow Volume=0.734c{{m}^{3}}\]

Now, volume of four conical depressions \[=4\times 0.734=2.93c{{m}^{3}}\]

$\therefore $ Volume of the wood in the entire stand $=525-2.93=522.07c{{m}^{3}}$

23. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see figure). The length of the entire capsule is $14mm$ and the diameter of the capsule is $5mm$. Find its surface area.

Ans: Given that the diameter of the capsule is $5mm$.

So the radius of a hemisphere is $r=2.5mm$ 

Height of cylinder is equal to the difference of total height to that of diameter of sphere.

We get

$\Rightarrow h=14-\left( 2.5+2.5 \right)=9mm$ 

Total surface area of the capsule is given by

$\Rightarrow 2\pi rh+2\left( 2\pi {{r}^{2}} \right)$ 

$\Rightarrow 2\pi \left( \dfrac{5}{2} \right)\left( 9 \right)+2\left( 2\pi {{\left( \dfrac{5}{2} \right)}^{2}} \right)$

$\Rightarrow 45\pi +25\pi $

$\Rightarrow 70\pi $

$\Rightarrow 70\times \dfrac{22}{7}$

$\Rightarrow \text{Surface area}=220m{{m}^{2}}$

Therefore, total surface area of capsule is $220m{{m}^{2}}$.

24. A spherical glass vessel has a cylindrical neck $8$ cm long, $2$ m in diameter, the diameter of the spherical part is $8.5$ cm. by measuring the amount of water it holds, a child finds its volume to be $345c{{m}^{3}}$, check whether she is correct, taking the above as side measurements. $\left[ \pi =3.14 \right]$. 

Ans: Given that a spherical glass vessel has a cylindrical neck $8$ cm long, $2$ m in diameter, and the diameter of the spherical part is $8.5$ cm.

Now, radius of cylindrical part is $r=1cm$ and height $h=8cm$ 

Radius of spherical part is $R=\dfrac{8.5}{2}=\dfrac{17}{4}cm$ 

Now, volume of glass solid is equal to the sum of volume of cylindrical part and volume of spherical part.

We get

$\Rightarrow Volume=\pi {{r}^{2}}h+\dfrac{4}{3}\pi {{R}^{3}}$ 

$\Rightarrow Volume=3.14\times {{\left( 1 \right)}^{2}}\times 8+\dfrac{4}{3}\times 3.14\times {{\left( \dfrac{17}{4} \right)}^{3}}$

$\Rightarrow Volume=3.14\left[ 8+\dfrac{4913}{48} \right]$

$\Rightarrow Volume=3.14\left[ \dfrac{384+4913}{48} \right]$

$\Rightarrow Volume=3.14\times \dfrac{5297}{48}$

$\Rightarrow Volume=3.14\times \dfrac{5297}{48}$

$\therefore Volume=346.51c{{m}^{3}}$

Therefore, the volume finds by the student is not correct.

25. Metallic spheres of radii $6$ cm, $8$ cm and $10$ cm respectively are melted to form a single solid sphere. Find the radius of the resulting sphere.

Ans: Let the radius of resulting sphere be $r\text{ }cm$.

As given in the question three metallic spheres melted and formed a single solid sphere.

So volume of resulting sphere is equal to the sum of volume of three spheres.

We get

$\Rightarrow \dfrac{4}{3}\pi {{r}^{3}}=\dfrac{4}{3}\pi {{\left( 6 \right)}^{3}}+\dfrac{4}{3}\pi {{\left( 8 \right)}^{3}}+\dfrac{4}{3}\pi {{\left( 10 \right)}^{3}}$ 

$\Rightarrow {{r}^{3}}={{\left( 6 \right)}^{3}}+{{\left( 8 \right)}^{3}}+{{\left( 10 \right)}^{3}}$

$\Rightarrow {{r}^{3}}=216+512+1000$

$\Rightarrow {{r}^{3}}=1728$

$\therefore r=12cm$

Therefore, radius of resulting sphere is $12cm$.

26. A shuttlecock used for playing badminton has the shape of a frustum of a cone mounted on a hemisphere. The external diameter of the frustum is $5$ cm and $2$ cm. The height of the entire shuttlecock is $7$ cm. Find the external surface area.

Ans: Given the diameters of a frustum of the cone are $5$ cm and $2$ cm.

So, radiuses are  ${{r}_{1}}=1cm$ and ${{r}_{2}}=2.5cm$ 

And the height of the shuttlecock is $7cm$. So the height of a cone is $h=7-1=6cm$ 

The external surface area of the shuttlecock is equal to the sum of the curved surface area of the cone and the surface area of the hemisphere.

We get

External surface area $=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l+2\pi r_{1}^{2}$ 

$\Rightarrow \pi \left( 2.5+1 \right)\sqrt{{{h}^{2}}+{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}}+2\pi \times 1$ 

\[\Rightarrow \pi \left( 3.5 \right)\sqrt{{{6}^{2}}+{{\left( 1-2.5 \right)}^{2}}}+2\pi \]

\[\Rightarrow \pi \left( 3.5 \right)\sqrt{36+2.25}+2\pi \]

\[\Rightarrow \pi \left( 3.5 \right)\sqrt{38.5}+2\pi \]

\[\Rightarrow \pi \left( 3.5 \right)6.18+2\pi \]

\[\Rightarrow 21.63\pi +2\pi \]

\[\Rightarrow 23.63\pi \]

\[\Rightarrow 23.63\times \dfrac{22}{7}\]

\[\Rightarrow 74.26c{{m}^{2}}\]

External surface area of shuttle cock is \[74.26c{{m}^{2}}\].

27. How many silver coins, $1.75$ cm in diameter and of thickness $2$ mm, must be melted to form a cuboid of dimensions \[\mathbf{5}.\mathbf{5cm}\times \mathbf{10cm}\times \mathbf{3}.\mathbf{5cm}\]?

Ans: Given, 

For silver coin, diameter is $1.75cm$ so radius is $\dfrac{1.75}{2}cm$ 

Thickness/height $=2mm=\dfrac{1}{5}cm$ 

For cuboid, dimensions are $5.5cm\times 10cm\times 3.5cm$ 

As given in the question silver coins are melted and formed a cuboid.

So the volume of coins is equal to the volume of cuboids.

Let the number of silver coins is $n$.

We get

$\Rightarrow n\times \pi {{r}^{2}}h=l\times b\times h$ 

$\Rightarrow n\times \dfrac{22}{7}{{\left( \dfrac{7}{8} \right)}^{2}}\times \dfrac{1}{5}=5.5\times 10\times 3.5$

$\Rightarrow n\times \dfrac{22}{7}\times \dfrac{49}{64}\times \dfrac{1}{5}=5.5\times 10\times 3.5$

$\Rightarrow n=\dfrac{5.5\times 10\times 3.5\times 7\times 64\times 5}{22\times 49}$

$\therefore n=400$

Therefore, $400$ silver coins must be melted.

28. A container like a right circular having a diameter $12$ cm and height $15$ cm is full of ice cream. The ice cream is to be filled in cones of height $12$ cm and diameter $6$ cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.

Ans: Given the diameter of the right circular container is $12$ cm and height $15$ cm.

Volume of cylinder is $\pi {{r}^{2}}h$.

We get

$\Rightarrow \pi {{\left( \dfrac{12}{2} \right)}^{2}}\times 15$ 

$\Rightarrow 540\pi $

Radius of cone is $r=6cm$ 

Volume of ice-cream is equal to the sum of volume of ice-cream cone and volume of hemispherical top of ice-cream.

We get

$\Rightarrow \dfrac{1}{3}\pi {{r}^{2}}h+\dfrac{2}{3}\pi {{r}^{3}}$ 

$\Rightarrow \dfrac{1}{3}\pi {{\left( 3 \right)}^{2}}\left( 12 \right)+\dfrac{2}{3}\pi {{\left( 3 \right)}^{3}}$

$\Rightarrow 36\pi +18\pi $

$\Rightarrow 54\pi $

$\therefore \text{Number of ice-cream}=\dfrac{\text{Volume of cylinder}}{\text{Volume of ice-cream+Volume of hemisphere}}$ 

We get

$\Rightarrow \text{Number of ice-cream}=\dfrac{540\pi }{54\pi }$

$\therefore \text{Number of ice-cream}=10\text{ ice-cream cones}$.

29. Water flowing at the rate of $15$ km per hour through a pipe of diameter $14$ cm into a rectangular tank which is $50$ m long and $44$ m wide. Find the time in which the level of water in the tank will rise by $21$ cm.

Ans: Given the diameter of the cylindrical pipe is $14$ cm.

Radius of pipe is $\dfrac{14}{2}=7cm$. 

So volume of cylinder is $\pi {{r}^{2}}h$ 

Water flows through pipe at the rate of $15$ km per hour.

We get

$\Rightarrow \dfrac{22}{7}\times \dfrac{7}{100}\times \dfrac{7}{100}\times 15000$ 

$\Rightarrow \dfrac{22}{7}\times \dfrac{7}{100}\times \dfrac{7}{100}\times 15000$

$\Rightarrow 231{{m}^{3}}$

Volume of tank is $=l\times b\times h$ 

Required volume of quantity of water in the tank is

$\Rightarrow 50\times 44\times \dfrac{21}{100}$

$\Rightarrow 462{{m}^{3}}$

Thus, $462{{m}^{3}}$ of water falls into tank in one hour.

Therefore, time taken by $462{{m}^{3}}$ of water to falls into tank is $\dfrac{1}{231}\times 462=2hours$. 

30. A solid cylinder of diameter $12$ cm and height $15$ cm is melted and recast into toys with the shape of a right circular cone mounted on a hemisphere of radius $3$ cm. If the height of the toy is $12$ cm, find the number of toys so formed.

Ans: Given, a solid cylinder is melted and recast into right circular cone.

$\Rightarrow \text{Number of toys}=\dfrac{\text{Volume of cylinder}}{\text{Volume of one toy}}$ 

We get

$\Rightarrow \dfrac{\pi {{R}^{2}}H}{\dfrac{2}{3}\pi {{r}^{3}}+\dfrac{1}{3}\pi {{r}^{2}}h}$ 

$\Rightarrow \dfrac{\pi {{R}^{2}}H}{\dfrac{1}{3}\pi {{r}^{2}}\left( 2r+h \right)}$

$\Rightarrow \dfrac{6\times 6\times 15}{\dfrac{1}{3}\times 3\times 3\left( 6+9 \right)}$

$\Rightarrow 12$ 

Therefore, number of toys is $12$. 

4 Marks Questions

1. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see figure). The length of the entire capsule is $14mm$ and the diameter of the capsule is $5mm$. Find its surface area.

Ans: Given that the diameter of the capsule is $5mm$.

So the radius of the hemisphere is $r=2.5mm$ 

Height of cylinder is equal to the difference of total height to that of diameter of sphere.

We get

$\Rightarrow h=14-\left( 2.5+2.5 \right)=9mm$ 

Total surface area of the capsule is given by

$\Rightarrow 2\pi rh+2\left( 2\pi {{r}^{2}} \right)$ 

$\Rightarrow 2\pi \left( \dfrac{5}{2} \right)\left( 9 \right)+2\left( 2\pi {{\left( \dfrac{5}{2} \right)}^{2}} \right)$

$\Rightarrow 45\pi +25\pi $

$\Rightarrow 70\pi $

$\Rightarrow 70\times \dfrac{22}{7}$

$\Rightarrow \text{Surface area}=220m{{m}^{2}}$

Therefore, total surface area of capsule is $220m{{m}^{2}}$.

2. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are $2.1$ m and $4$ m respectively and the slant height of the top is $2.8$ m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs. $500\text{ }per\text{ }{{m}^{2}}$ . (Note that the base of the tent will not be covered with canvas.)

Ans: Given, the diameter of the cylindrical part is $2.1$ m and $4$ m respectively and the slant height of the top is $2.8$ m.

The total surface area of the tent is the sum of the curved surface area of the cylindrical part and the curved surface area of the conical cap.

We get,

$\Rightarrow 2\pi \times 2\times 2.1+\pi \times 2\times 2.8$ 

$\Rightarrow 8.4\pi +5.6\pi $

$\Rightarrow 8.4\pi +5.6\pi $

$\Rightarrow 14\pi $

$\Rightarrow 14\times \dfrac{22}{7}$

$\Rightarrow 44{{m}^{2}}$

Canvas of the tent at the rate of Rs. $500\text{ }per\text{ }{{m}^{2}}$. 

So the total cost of canvas is $44\times 500=22000$ 

So cost of canvas of tent is $Rs.22000$.  

3. From a solid cylinder whose height is $2.4$ cm and diameter $1.4$ cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest $c{{m}^{2}}$.

Ans: Given, the height of solid cylinder is $2.4$ cm and diameter $1.4$ cm.

Radius of solid cylinder is $0.7cm$ and radius of base of conical cavity is $0.7cm$.

Slant height of conical cavity is $\sqrt{{{\left( 0.7 \right)}^{2}}+{{\left( 2.4 \right)}^{2}}}$ 

We get

$\Rightarrow \sqrt{0.49+5.76}$ 

\[\Rightarrow \sqrt{6.25}\]

\[\Rightarrow 2.5cm\]

Total surface area of remaining solid is 

$\Rightarrow 2\pi \left( 0.7 \right)\left( 2.4 \right)+\pi {{\left( 0.7 \right)}^{2}}+\pi \left( 0.7 \right)\left( 2.5 \right)$ 

$\Rightarrow 3.36\pi +0.49\pi +1.75\pi $

$\Rightarrow 5.6\pi $

$\Rightarrow 5.6\times \dfrac{22}{7}$

$\Rightarrow 17.6c{{m}^{2}}$

Therefore, the total surface area of the remaining solid to the nearest centimetre square is $18c{{m}^{2}}$.

4. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder as shown in the figure. If the height of the cylinder is $10cm$ and its base is of radius $3.5$ cm, find the total surface area of the article.

Ans: Given that the height of the cylinder is $10cm$ and its base is of radius $3.5$ cm.

Total surface area of the article is given by

$\Rightarrow 2\pi rH+2\left( 2\pi {{r}^{2}} \right)$ 

$\Rightarrow 2\pi \left( 3.5 \right)\left( 10 \right)+2\left( 2\pi {{\left( 3.5 \right)}^{2}} \right)$

$\Rightarrow 70\pi +49\pi $

$\Rightarrow 119\pi $

$\Rightarrow 119\times \dfrac{22}{7}$

$\therefore TSA=374c{{m}^{2}}$

Therefore, total surface area of article is $374c{{m}^{2}}$. 

5. Derive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.

Ans: According to the question, the frustum is difference of the two cones $OAB$ and $OCD$ (in figure).

Let $h$ be the height, $l$ be the slant height and ${{r}_{1}}$ and ${{r}_{2}}$ be the radii of bases of a frustum.

Then from figure,

$OA=OB=l$ and $OP={{h}_{1}}$ 

$\therefore \text{height of the cone}={{h}_{1}}-h$ 

$\because \Delta OQD\sim \Delta OPB$ [by AA similarity]

We get

$\Rightarrow \dfrac{{{h}_{1}}-h}{{{h}_{1}}}=\dfrac{{{r}_{2}}}{{{r}_{1}}}$

$\Rightarrow 1-\dfrac{h}{{{h}_{1}}}=\dfrac{{{r}_{2}}}{{{r}_{1}}}$

$\Rightarrow 1-\dfrac{{{r}_{2}}}{{{r}_{1}}}=\dfrac{h}{{{h}_{1}}}$

$\Rightarrow {{h}_{1}}=\dfrac{h{{r}_{1}}}{{{r}_{1}}-{{r}_{2}}}$ ……..(1)

$\therefore \text{height of the cone OCD}={{h}_{1}}-h$

We get

$\Rightarrow \dfrac{h{{r}_{1}}}{{{r}_{1}}-{{r}_{2}}}-h=\dfrac{h{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}}$   ……..(2)

Volume of frustum is equal to the difference of volumes of both the cones.

We get

$\Rightarrow \text{Volume of frustum}=\dfrac{1}{3}\pi {{r}_{1}}^{2}{{h}_{1}}-\dfrac{1}{3}\pi {{r}_{2}}^{2}\left( {{h}_{1}}-h \right)$ 

Substitute values from eq.(1) and (2) we get

$\Rightarrow \text{Volume of frustum}=\dfrac{\pi }{3}\left[ {{r}_{1}}^{2}\dfrac{h{{r}_{1}}}{{{r}_{1}}-{{r}_{2}}}-{{r}_{2}}^{2}\dfrac{h{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}} \right]$

$\Rightarrow \text{Volume of frustum}=\dfrac{\pi h}{3}\left[ \dfrac{{{r}_{1}}^{3}}{{{r}_{1}}-{{r}_{2}}}-\dfrac{{{r}_{2}}^{3}}{{{r}_{1}}-{{r}_{2}}} \right]$

$\Rightarrow \text{Volume of frustum}=\dfrac{1}{3}\pi h\left[ {{r}_{1}}^{2}+{{r}_{2}}^{2}+{{r}_{1}}{{r}_{2}} \right]$

Let ${{A}_{1}}$ and ${{A}_{2}}$ be the surface areas of two circular bases.

We get

${{A}_{1}}=\pi {{r}_{1}}^{2}$ and ${{A}_{2}}=\pi {{r}_{2}}^{2}$

$\therefore \text{Volume of frustum}=\dfrac{1}{3}h\left[ \pi {{r}_{1}}^{2}+\pi {{r}_{2}}^{2}+\sqrt{\pi {{r}_{1}}^{2}}\sqrt{\pi {{r}_{2}}^{2}} \right]$

$\therefore \text{Volume of frustum}=\dfrac{h}{3}\left[ {{A}_{1}}+{{A}_{2}}+\sqrt{{{A}_{1}}{{A}_{2}}} \right]$

From figure, in $\Delta DEB$,

$\Rightarrow l=\sqrt{{{h}^{2}}+{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}}$  

$\because \Delta OQD\sim \Delta OPB$ [by AA similarity]

We get

$\Rightarrow \dfrac{{{l}_{1}}-l}{{{l}_{1}}}=\dfrac{{{r}_{2}}}{{{r}_{1}}}$

$\Rightarrow {{l}_{1}}=\dfrac{l{{r}_{1}}}{{{r}_{1}}-{{r}_{2}}}$ ……..(3)

$\therefore length\text{ of the cone OCD}={{l}_{1}}-l$

We get

$\Rightarrow \dfrac{l{{r}_{1}}}{{{r}_{1}}-{{r}_{2}}}-l=\dfrac{l{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}}$   ……..(4)

Now, curved surface area of frustum of cone is 

$\Rightarrow CSA=\pi {{r}_{1}}{{l}_{1}}-\pi {{r}_{2}}\left( {{l}_{1}}-l \right)$ 

Substitute values from eq.(3) and (4) we get

$\Rightarrow CSA=\pi {{r}_{1}}\dfrac{l{{r}_{1}}}{{{r}_{1}}-{{r}_{2}}}-\pi {{r}_{2}}\dfrac{l{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}}$

$\Rightarrow CSA=\pi l\left[ \dfrac{{{r}_{1}}^{2}-{{r}_{2}}^{2}}{{{r}_{1}}-{{r}_{2}}} \right]$

\[\Rightarrow CSA=\pi l\left( {{r}_{1}}+{{r}_{2}} \right)\], where $l=\sqrt{{{h}^{2}}+{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}}$

Therefore, total surface area of frustum of cone is \[\pi l\left( {{r}_{1}}+{{r}_{2}} \right)+\pi {{r}_{1}}^{2}+\pi {{r}_{2}}^{2}\].

6. A bucket made up of a metal sheet is in the form of a frustum of a cone. Its depth is $24cm$ and the diameters of the top and bottom are $30$ cm and $10$ cm respectively. Find the cost of milk which will completely fill the bucket at the rate of Rs. $20$ per litre and cost of metal sheet used if it costs \[Rs.10\text{ per 100 c}{{\text{m}}^{\text{2}}}\].

Ans: Given the diameters of top and bottom of a frustum cone are $30$ cm and $10$ cm.

So radiuses of two ends of a frustum cone are $15$ cm and $5$ cm.

${{r}_{1}}=15cm$ and ${{r}_{2}}=5cm$ 

Height $=24cm$ 

Now, volume of bucket is 

\[\Rightarrow \dfrac{1}{3}\pi h\left[ r_{1}^{2}+r_{2}^{2}+{{r}_{1}}{{r}_{2}} \right]\] 

\[\Rightarrow \dfrac{1}{3}\times 3.14\times 24\left[ {{15}^{2}}+{{5}^{2}}+15\times 5 \right]\]

\[\Rightarrow \dfrac{1}{3}\times 3.14\times 24\left[ 225+25+75 \right]\]

\[\Rightarrow \dfrac{1}{3}\times 3.14\times 24\times 325\]

\[\Rightarrow 8164c{{m}^{3}}=8.164liters\] 

Given cost of one liter of milk is $Rs.20$ 

Total cost of milk is $8.164\times 20=163.28$ 

Cost of milk is $Rs.163.28$ 

Surface area of bucket $=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l+\pi r_{2}^{2}$ 

$\Rightarrow \text{Surface area}=\pi \left( {{r}_{1}}+{{r}_{2}} \right)\sqrt{{{\left( {{r}_{1}}-{{r}_{2}} \right)}^{2}}+{{h}^{2}}}+\pi r_{2}^{2}$

$\Rightarrow \text{Surface area}=3.14\left( 15+5 \right)\sqrt{{{\left( 15-5 \right)}^{2}}+{{24}^{2}}}+3.14{{\left( 5 \right)}^{2}}$

\[\Rightarrow \text{Surface area}=3.14\times 20\sqrt{100+576}+3.14\times 25\]

\[\Rightarrow \text{Surface area}=3.14\times 20\times 26+78.5\]

$\Rightarrow \text{Surface area}=1632.8+78.5$

$\therefore \text{Surface area}=1711.3c{{m}^{2}}$

Cost of metal sheet is \[Rs.10\text{ per 100 c}{{\text{m}}^{\text{2}}}\].

Total cost of metal sheet is $1711.3\times \dfrac{10}{100}=171.13$ 

Therefore, cost of metal sheet is $Rs.171.13$. 

7. A solid consisting of a right circular cone standing on a hemisphere is placed upright in a right circular cylinder, full of water and touches the bottom. Find the volume of water left in the cylinder having given that the radius of the cylinder is $3cm$ and its height is $6cm$. The radius of a hemisphere is $2cm$ and the height of the cone is $4cm$. Give your answer to the nearest cubic centimeters. $\left( \pi =\dfrac{22}{7} \right)$.

Ans: Given, the radius of the cylinder is $3cm$ and its height is $6cm$.

Volume of cylinder is $\pi {{\left( 3 \right)}^{2}}6=54\pi $ 

Given, radius of hemisphere is $2cm$ and height is $4cm$.

Volume of hemisphere is $\dfrac{1}{2}\times \dfrac{4}{3}\pi {{\left( 2 \right)}^{3}}=\dfrac{16}{3}\pi $ 

Volume of cone is $\dfrac{1}{3}\pi {{\left( 2 \right)}^{2}}4=\dfrac{16}{3}\pi $ 

Volume of water left in the cylinder is

$\Rightarrow 54\pi -\dfrac{16}{3}\pi -\dfrac{16}{3}\pi $ 

$\Rightarrow \left( \dfrac{162-16-16}{3} \right)\pi $

$\Rightarrow \dfrac{2860}{21}c{{m}^{3}}$

$\Rightarrow 136\dfrac{4}{21}c{{m}^{3}}$

Therefore, the volume of water to the nearest cubic centimetres is $136c{{m}^{3}}$.

8. A farmer connects a pipe of internal diameter $20cm$ from a canal into a cylindrical tank in his field which is $10m$ in diameter and $2m$ deep. If water flows through the pipe at the rate of $3km/h$, in how much time will the tank be filled?

Ans: Given, rate of water flowing $=3km/hr=\dfrac{5}{6}m/\sec $ 

So in one second $\dfrac{5}{6}m$ water flows

Internal diameter of pipe is $20cm=\dfrac{1}{5}m$.

So volume of water flows through the pipe in one second is

$\Rightarrow \pi {{r}^{2}}h$ 

$\Rightarrow \dfrac{22}{7}\times {{\left( \dfrac{1}{10} \right)}^{2}}\times \dfrac{5}{6}$

$\Rightarrow \dfrac{11}{420}{{m}^{3}}$

Given the diameter of tank is $10m$ and height is $2m$. 

Volume of water in tank is

$\Rightarrow \pi {{r}^{2}}h$ 

$\Rightarrow \dfrac{22}{7}\times {{\left( \dfrac{10}{2} \right)}^{2}}\times 2$

$\Rightarrow \dfrac{1100}{7}{{m}^{3}}$

Time taken to fill the tank is $\dfrac{\dfrac{1100}{7}}{\dfrac{11}{420}}$ .

We get

$\Rightarrow \dfrac{1100\times 420}{7\times 11}=100\text{minute}$ 

Therefore, time taken to fill the tank is $\text{1 hour 40 minutes}$. 

9. A cone of radius $10cm$ is divided into two parts by drawing a plane through the midpoint of its axis, parallel to its base. Compare the volume of the two parts.

Ans: Let $OAB$ be the cone and $OQ$ be its axis and $P$ be the mid-point of $OQ$. 

Let $OQ=h\text{ }cm$ 

Then, $OP=PQ=\dfrac{h}{2}cm$ 

And radius of cone $QB=10cm$ 

Also $\Delta OPD\sim \Delta OQB$ 

$\therefore \dfrac{OP}{OQ}=\dfrac{PD}{QB}$ 

$\Rightarrow \dfrac{{h}/{2}\;}{h}=\dfrac{PD}{10}$ 

$\Rightarrow PD=5cm$

For smaller cone radius $r=5cm$ and height $h=\dfrac{h}{2}cm$ 

Volume of smaller cone is $\dfrac{1}{3}\pi \times {{\left( 5 \right)}^{2}}\dfrac{h}{2}=\dfrac{25\pi h}{6}c{{m}^{3}}$  

Now, for frustum of cone radius $R=10cm$, $r=5cm$ and height $h=\dfrac{h}{2}cm$ 

Volume of frustum of cone is  

$\Rightarrow \dfrac{1}{3}\pi \dfrac{h}{2}\left[ {{\left( 10 \right)}^{2}}+{{\left( 5 \right)}^{2}}+10\times 5 \right]$ 

$\Rightarrow \dfrac{1}{3}\pi \dfrac{h}{2}\left[ 100+25+50 \right]$

$\Rightarrow \dfrac{1}{3}\pi \dfrac{175h}{2}$

\[\Rightarrow Volume=\dfrac{175\pi h}{6}c{{m}^{3}}\]

Required ratio of volumes is

$\Rightarrow \dfrac{25\pi h}{6}:\dfrac{175\pi h}{6}$ 

$\Rightarrow 25:175$

$\therefore Ratio=1:7$

CBSE Class 10 Maths Important Questions Chapter 12 - Free PDF Download

Chapter 12 will help the students understand the concepts of surface areas and volumes of different shapes like sphere, cone, cylinder, etc. The surface area and volume class 10 important questions will help the students practice the concepts they have learned in this chapter. Maths is a subject that requires not only the understanding of the concept but also a revision of these concepts through practice questions. Solving these important questions will help the students to cover all the important topics from the chapter.

The surface area and volume questions have been compiled along with their detailed step by step answers. Students can check their answers and can also understand what necessary steps are required to be provided in the answers. Surface area and volume class 10 CBSE important questions pdf can be easily downloaded by the students for referring while they are preparing for their exams. Sometimes a concept in maths becomes clear only after the student has solved practical questions based on it. The important questions of chapter 12 will clear all the doubts of the students and help strengthen their basics about the topic surface area and volumes.

These important questions will not only help the students in the class 10 board exams but also in their class tests. When students are trying to solve maths questions, they can derive the answer but do not provide all the necessary steps that must be written in the exam to score good marks. With the help of the solutions to these important questions, students will not miss out on any steps while solving the questions. 

Topics Covered by the Surface Area and Volume Class 10 CBSE Important Questions

Chapter 12 class 10 Maths helps the students understand concepts related to the topic surface area and volumes of different shapes. It also covers the conversion of a solid from one shape to another and finding the surface area and volume of this new shape. The important questions compiled by Vedantu cover:

• Introduction to surface area and volumes

• Surface area of a combination of solids

• Volume of a combination of solids

• Conversion of a solid from one shape to another shape

• Frustum of a cone

Sometimes a complex solid figure is made up of a combination of two or more basic solid figures. Such a complex figure can be broken down into simpler figures and area can be calculated for these simple figures. Students will learn how to find the volume of solids and the volume of solids that have been formed by joining two simple or basic solids. The important questions help the students understand how to find the radius and the volume when one shape is converted to another shape, or when a liquid from one container of a particular shape is transferred to another container of a different shape. When a cone is cut with a plane parallel to its base, and the cone formed on the other side of this plane is removed, the part left is called the frustum of the cone. The questions help understand how to find the volume of a cone’s frustum.

Practice Questions of Chapter 12

Mentioned below are some of the practice questions that can help students in their preparations for the upcoming board examinations.

Question 1

The hemisphere's radius is 3.5 cm, while the cone's height is 4 cm. The solid is placed in a cylindrical tub filled with water such that it is completely submerged in water. Find the volume of water left in the cylindrical tub if the radius of the tub is 5 cm and the height is 10.5 cm.

Answer: 683.8 cm3 

Question 2

The dimensions of a canal is given as 300 cm wide and 120 cm deep. The speed of water moving through it is 20 km/h. Calculate the area irrigated in 20 minutes if 8 cm of standing water is desired? 

Answer: 30 hectares

Question 3

Calculate how many solid spheres with a diameter of 6 cm may be formed by melting a solid metal cylinder with a height of 45 cm and a diameter of 4 cm.

Answer: 5

Question 4

A solid hemisphere's volume and surface area are Mathematically equal. What is the hemisphere's diameter?

Answer: 6 cm 

Question 5

The curved surface area of a right circular cone with a radius of 3 cm is 47.1 cm2. Calculate the cone's volume.

Answer: 37.68 cm3

Benefits of the Important Questions for Class 10 Maths Chapter 12

1. Expert Compilation: The questions are meticulously compiled by experts after thorough research on previous years' papers.

2. CBSE Guideline Adherence: Solved in alignment with CBSE guidelines, the questions serve as valuable guides, illustrating the proper methods for solving specific question types.

3. Concept Mastery: These important questions aid students in becoming proficient in tackling various question formats related to the surface area and volume concepts.

There can be trick questions based on a topic in the exam. By practising these important questions students will be prepared for all kinds of questions.

Important Related Links for CBSE Class 10 Maths