NCERT Exemplar for Class 10 Maths - Surface Areas and Volumes - Free PDF Download
Download free PDF of NCERT Exemplar for Class 10 Maths Chapter 12 - Surface Areas and Volumes solved by expert Maths teachers from Vedantu.com. These solutions are designed as per NCERT (CBSE) Book guidelines. All Chapter 12 - Surface Areas and Volumes exercise questions with solutions will help you to revise and complete the syllabus and score more marks in your examinations.
Vedantu is a platform that provides free CBSE Solutions and other study materials for students. You can download NCERT Solutions for Class 10 Maths to help you to revise the complete Syllabus and score more marks in your examinations. Subjects like Science, Maths, Engish will become easy to study if you have access to NCERT Solution for Class 10 Science, Maths solutions, and solutions of other subjects that are available on Vedantu only.
Access NCERT Exemplar Solutions for class 10 Mathematics Chapter 12 - Surface Areas And Volumes
Multiple Choice Questions :
Choose the correct answer from the given four options:
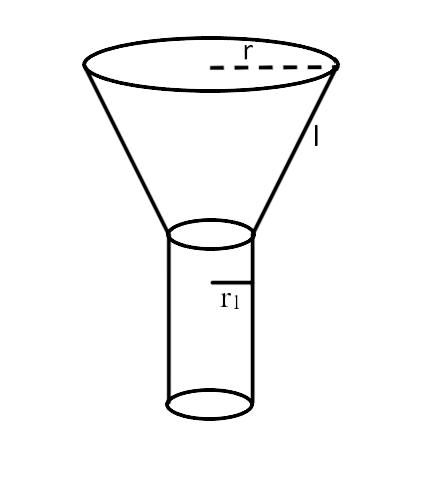
Sample Question 1: A funnel is the combination of
(a) a cone and a cylinder
(b) frustum of a cone and a cylinder
(c) a hemisphere and a cylinder
(d) a hemisphere and a cone
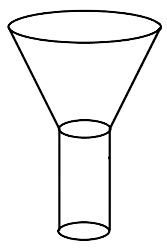
Ans: The correct answer is option (b) frustum of a cone and a cylinder.
On observing the given figure the funnel is a combination of frustum of a cone and a cylinder.
Sample Question 2: If a marble of radius 2.1 cm is put into a cylindrical cup full of water of radius 5 cm and height 6 cm, then how much water flows out of the cylindrical cup?
(a) $$38.8\,\,c{m^3}$$
(b) $$55.4\,\,c{m^3}$$
(c) $$19.4\,\,c{m^3}$$
(d) $$471.4\,\,c{m^3}$$
Ans: The correction option is (a) $$38.8\,\,c{m^3}$$.
By using the volume of a sphere formula we get
$$V = \dfrac{4}{3}\pi {r^3}$$
$$ = \dfrac{4}{3} \times 3.14 \times {(2.1)^2}$$
$$ = 38.8\,c{m^3}$$
Sample Question 3: A cubical ice cream brick of edge 22 cm is to be distributed among some children by filling ice cream cones of radius 2 cm and height 7 cm upto its brim. How many children will get the ice cream cones?
(a) 163
(b) 263
(c) 363
(d) 463
Ans: The correct option is (c) 363.
$$\text{Number of ice-cream cones} = \dfrac{\text{Volume of cubical ice cream brick}}{\text{Volume of each ice-cream cone}}$$
$$ = \dfrac{{{a^3}}}{{\dfrac{1}{3}\pi {r^2}h}}$$
$$ = \dfrac{{22 \times 22 \times 22}}{{\dfrac{1}{3} \times \dfrac{{22}}{7} \times 7 \times 2 \times 2}}$$
$$ = \dfrac{{22 \times 22 \times 22 \times 7 \times 3}}{{22 \times 7 \times 2 \times 2}}$$
$$ = 363$$
Sample Question 4: The radii of the ends of a frustum of a cone of height h cm are $${r_1}$$ cm and $${r_2}$$ cm. The volume in $$c{m^3}$$ of the frustum of the cone is
(a) $$\dfrac{1}{3}\pi h[r_1^2 + r_2^2 + {r_1}{r_2}]$$
(b) $$\dfrac{1}{3}\pi h[r_1^2 + r_2^2 - {r_1}{r_2}]$$
(c) $$\dfrac{1}{3}\pi h[r_1^2 - r_2^2 + {r_1}{r_2}]$$
(d) $$\dfrac{1}{3}\pi h[r_1^2 - r_2^2 - {r_1}{r_2}]$$
Ans: The correct answer is option (a) $$\dfrac{1}{3}\pi h[r_1^2 + r_2^2 + {r_1}{r_2}]$$.
We know that, the volume of the frustum cone is $$ = \dfrac{1}{3}\pi h[r_1^2 + r_2^2 + {r_1}{r_2}]\,\,c{m^3}$$
Sample Question 5: The volume of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
(a) $$9.7\,\,c{m^3}$$
(b) $$77.6\,\,c{m^3}$$
(c) $$58.2\,\,c{m^3}$$
(d) $$19.4\,\,c{m^3}$$
Ans: The correct option is (d) $$19.4\,\,c{m^3}$$.
Radius of cone is 2.1 cm and height of cone is 4.2 cm
$$\text{Volume of cone} = \dfrac{1}{3}\pi {r^2}h$$
$$ = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 2.1 \times 2.1 \times 4.2$$
$$ = 19.4\,\,c{m^3}$$
Exercise - 12.1
Choose the correct answer from the given four options in the following questions:
1. A cylindrical pencil sharpened at one edge is the combinations of
(a) a cone and a cylinder
(b) frustum of a cone and a cylinder
(c) a hemisphere and a cylinder
(d) two cylinders.
Ans: The correct option is (a) a cone and a cylinder.
A one edge sharped cylindrical pencil is the combination of the shapes at the sharpened part is cone and unsharpened part is cylinder.

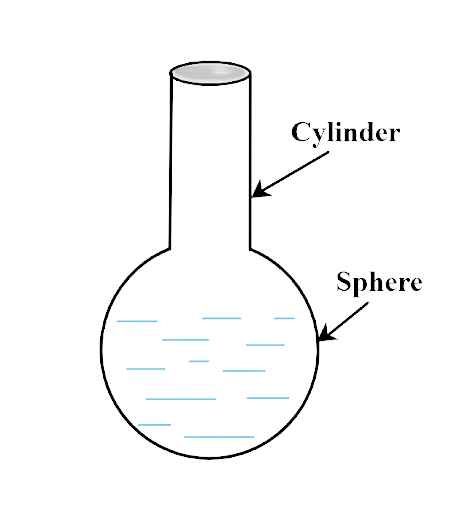
2. A surahi is the combination of
(a) a sphere and a cylinder
(b) a hemisphere and a cylinder
(c) two hemispheres
(d) a cylinder and a cone
Ans: The correct option is (a) a sphere and a cylinder.
Surahi is an Indian clay pot with a long cylindrical shaped neck and sphere at the bottom used for storing water.
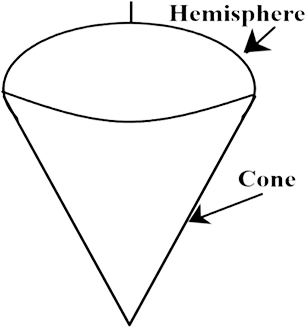
3. A plumbline (Sahul) is the combination of
(a) a cone and a cylinder
(b) a hemisphere and a cone
(c) frustum of a cone and a cylinder
(d) sphere and cylinder
Ans: The correct option is (b) a hemisphere and a cone.
A plumbline is a line with a plumb attached to it, used as an instrument for finding the depth of water or verticality of an object. It seems like a combination of hemisphere shape on top and a cone shape on bottom.
4.The shape of a glass (tumbler) (see figure) is usually in the form of a
(a) Cone
(b) Frustum of a cone
(c) Cylinder
(d) Sphere
Ans: The correct option is (b) Frustum of a cone.
The given figure seems like a cone but if cut by a plane horizontally, parallel to the base, The upper part of the cone remains the same in its shape but the bottom part makes a frustum.
5. The shape of a gilli, in the gilli - danda game (see in figure) is a combination of

(a) two cylinders
(b) a cone and a cylinder
(c) two cones and a cylinder
(d) two cylinders and a cone
Ans: The correct option is (c) two cones and a cylinder.
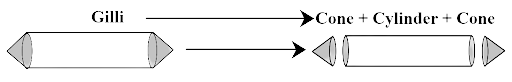
In the given figure gilli had two sharped edges that are like cone shapes and between the two edges cylinder shape is there. So, the shape of a gilli, in the gilli - danda game is a combination of two cones and a cylinder.
6. A shuttle cock used for playing badminton has the shape of the combination of
(a) a cylinder and a sphere
(b) a cylinder and a hemisphere
(c) a sphere and a cone
(d) frustum of a cone and a hemisphere
Ans: The correct option is (d) frustum of a cone and a hemisphere.
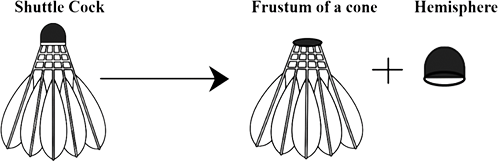
A shuttle cock used for playing badminton. If we cut it parallel to the base, which has the shape of the combination of frustum of a cone and a hemisphere.
7. A cone is cut through a plane parallel to its base and then the cone formed on one side of that plane is removed. The new part that is left over on the other side of the plane is called
(a) a frustum of cone
(b) cone
(c) Cylinder
(d) Sphere
Ans: The correct option is (a) a frustum of a cone.
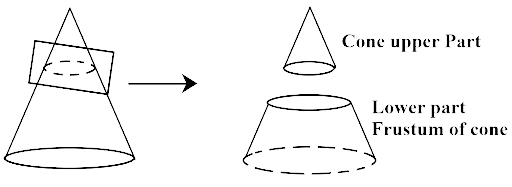
If any cone is cut through a plane parallel to its base which formed the cone in the upper part and a new part that is left over at the bottom side of a plane is called as a frustum of the cone.
8. A hollow cube of internal edge $$22$$ cm is filled with spherical marbles of diameter $$0.5$$ cm and it is assumed that $$\dfrac{1}{8}$$ space of the cube remains unfilled. Then the number of marbles that the cube can accommodate is
(a) $$142296$$
(b) $$142396$$
(c) $$142496$$
(d) $$142596$$
Ans: The correct option is (a) $$142296$$.
Let us consider the spherical marble has radius ‘$$r$$’ cm
Given, the diameter of marble $$ = 0.5$$ cm
$$ \Rightarrow \text{radius} = \dfrac{\text{diameter}}{2} = \dfrac{{0.5}}{2}\,cm$$
$$ \Rightarrow \,\,\,r = 0.25\,cm$$
Given the length of a cube $$l = 22\,cm$$
Let ‘$$n$$’ numbers of marbles can fill the cube. But, the $$\dfrac{1}{8}$$ space of the cube remains unfilled.
$$\therefore \text{Volume of 'n' marbles} = \left( {1 - \dfrac{1}{8}} \right)\text{Part of volume of cube}$$
As we know that,
$$\text{Volume of spherical marbles} = \dfrac{4}{3}\pi {r^3}$$
$$\text{Volume of cube} = {l^3}$$, then
$$ \Rightarrow \,\,\,n \times \dfrac{4}{3}\pi {r^3} = \left( {1 - \dfrac{1}{8}} \right)\,\,{l^3}$$
$$ \Rightarrow \,\,\,n \times \dfrac{4}{3}\pi {r^3} = \dfrac{7}{8} \times \,\,{22^3}$$
$$ \Rightarrow \,\,\,n = \dfrac{{7{l^3}}}{8} \times \,\dfrac{3}{{4\pi {r^3}}}$$
Substitute, $$\pi = \dfrac{{22}}{7}$$, $$r = 0.25\,cm$$ and $$l = 22\,cm$$.
$$ \Rightarrow \,\,\,n = \dfrac{{7 \times {{\left( {22} \right)}^3}}}{8} \times \,\dfrac{3}{{4\left( {\dfrac{{22}}{7}} \right){{\left( {0.25} \right)}^3}}}$$
$$ \Rightarrow \,\,\,n = \dfrac{{7 \times 22 \times 22 \times 22 \times 3 \times 7}}{{8 \times 4 \times 22 \times 0.25 \times 0.25 \times 0.25}}$$
$$ \Rightarrow \,\,\,n = \dfrac{{1565256}}{{11}}$$
On simplification, we get
$$\therefore \,\,\,n = 142296$$ marbles.
9. A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form of a cone of base diameter 8 cm. The height of the cone is
(a) 12 cm
(b) 14 cm
(c) 15 cm
(d) 18 cm
Ans: The correct option is (b) 14 cm.
Spherical shell
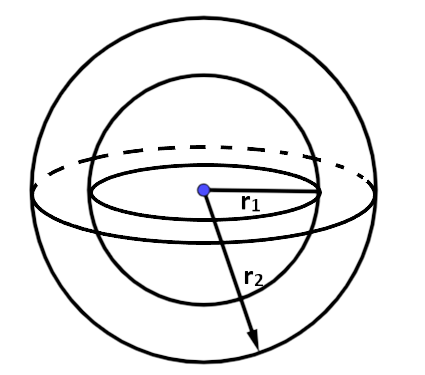
$${r_1} = \dfrac{4}{2} = 2\,cm$$
$${r_2} = \dfrac{8}{2} = 4\,cm$$
Cone
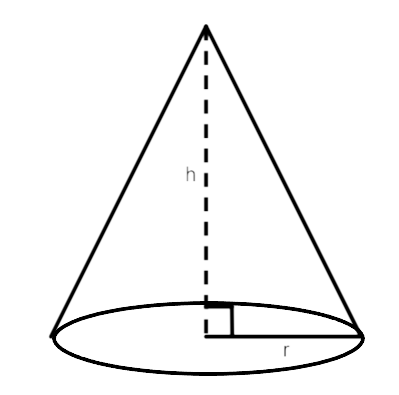
$$r = \dfrac{8}{2} = 4\,cm$$
$$h = ?$$
Remember that the volume of a shape does not change when it is recast into another.
$$\therefore $$ Volume of cone = Volume of hollow spherical shell
$$ \Rightarrow \,\,\dfrac{1}{3}\pi {r^2}h = \dfrac{4}{3}\pi r_2^3 - \dfrac{4}{3}\pi r_1^3$$
$$ \Rightarrow \,\,\dfrac{1}{3}\pi {r^2}h = \dfrac{4}{3}\pi \left( {r_2^3 - r_1^3} \right)$$
On canceling $$\dfrac{\pi }{3}$$ on both side, then
$$ \Rightarrow \,\,{r^2}h = 4\left( {r_2^3 - r_1^3} \right)$$
$$ \Rightarrow \,\,{4^2} \times h = 4 \times \left( {{{\left( 4 \right)}^3} - {{\left( 2 \right)}^3}} \right)$$
$$ \Rightarrow \,\,4h = 64 - 8$$
$$ \Rightarrow \,\,4h = 56$$
$$ \Rightarrow \,\,h = \dfrac{{56}}{4}$$
$$\therefore \,\,\,\,h = 16\,\,cm$$
10. A solid piece of iron in the form of a cuboid of dimensions 49 cm × 33cm × 24 cm, is moulded to form a solid sphere. The radius of the sphere is
(a) 21 cm
(b) 23 cm
(c) 25 cm
(d) 19 cm
Ans: The correct option is (a) 21 cm.
A solid iron cuboid is moulded into a solid sphere. As a result, the volume of a cuboid and a sphere are equal.
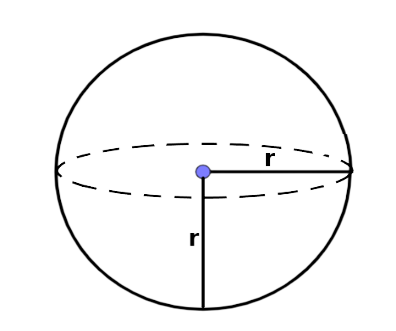
Sphere
$$r = ?$$
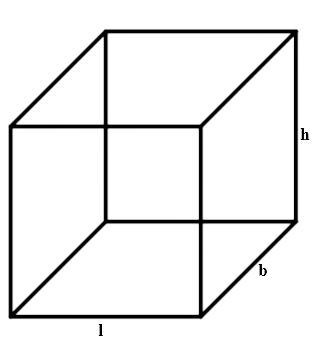
Cuboid
$$l = 49\,cm$$
$$b = 33\,cm$$
$$h = 24\,cm$$
$$\therefore $$ Volume of sphere (solid) = Volume of cuboid
$$ \Rightarrow \,\,\dfrac{4}{3}\pi {r^3} = l \times b \times h$$
$$ \Rightarrow \,\,{r^3} = \dfrac{{l \times b \times h \times 3}}{{4 \times \pi }}$$
$$ \Rightarrow \,\,{r^3} = \dfrac{{49 \times 33 \times 24 \times 3}}{{4 \times \left( {\dfrac{{22}}{7}} \right)}}$$
$$ \Rightarrow \,\,{r^3} = \dfrac{{49 \times 33 \times 24 \times 3 \times 7}}{{4 \times 22}}$$
$$ \Rightarrow \,\,{r^3} = \dfrac{{49 \times 3 \times 24 \times 3 \times 7}}{{4 \times 2}}$$
$$ \Rightarrow \,\,{r^3} = \dfrac{{49 \times 3 \times 24 \times 3 \times 7}}{8}$$
$$ \Rightarrow \,\,{r^3} = 49 \times 3 \times 3 \times 3 \times 7$$
$$ \Rightarrow \,\,{r^3} = 7 \times 7 \times 7 \times 3 \times 3 \times 3$$
$$ \Rightarrow \,\,{r^3} = {7^3} \times {3^3}$$
$$ \Rightarrow \,\,r = 7 \times 3$$
$$\therefore \,\,r = 21\,\,cm$$
11. A mason construction a wall of dimensions 270 cm × 300 cm × 350 cm with the bricks each of size 22.5 cm × 11.25 cm × 8.75 cm and it is assumed that $$\dfrac{1}{8}$$ space is covered by the mortar. Then the number of bricks used to construct the wall is
(a) 11100
(b) 11200
(c) 11000
(d) 11300
Ans: The correct option is (b) 11200
Given, the volume of the wall covered by $$ = \dfrac{1}{8}$$ mortar part
So, the volume covered by bricks of wall $$ = \left( {1 - \dfrac{1}{8}} \right)$$ volume of wall
$$\therefore $$ The volume covered by bricks of wall $$ = \dfrac{7}{8}$$ volume of wall
Given, size of bricks (cuboid in shape) : $${l_1} = 22.5\,cm$$, $${b_1} = 11.25\,cm$$ and $${h_1} = 8.75\,cm$$
Size of wall (cuboid in shape) : $$l = 270\,cm$$, $$b = 300\,cm$$ and $$h = 350\,cm$$
Let ‘n’ be the number of bricks in the wall, then
Volume of ‘n’ bricks $$ = \dfrac{7}{8}$$ volume of wall
$$ \Rightarrow \,\,n \times {l_1} \times {b_1} \times {h_1} = \dfrac{7}{8} \times l \times b \times h$$
$$ \Rightarrow \,\,n = \dfrac{{7 \times l \times b \times h}}{{8 \times {l_1} \times {b_1} \times {h_1}}}$$
$$ \Rightarrow \,\,n = \dfrac{{7 \times 270 \times 300 \times 350}}{{8 \times 22.5 \times 11.25 \times 8.75}}$$
$$ \Rightarrow \,\,n = \dfrac{{7 \times 270 \times 300 \times 350 \times 10 \times 100 \times 100}}{{8 \times 225 \times 1125 \times 875}}$$
$$ \Rightarrow \,\,n = \dfrac{{7 \times 270 \times 300 \times 350 \times 10 \times 100 \times 100}}{{8 \times 225 \times 1125 \times 875}}$$
$$ \Rightarrow \,\,n = 14 \times 2 \times 100 \times 4$$
$$\therefore \,\,n = 11200$$ bricks.
12. Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is
(a) 4 cm
(b) 3 cm
(c) 2 cm
(d) 6 cm
Ans: The correct option is (c) 2 cm.
Given, a solid metallic cylinder is melted to become 12 solid spheres of the same size.
So, the volume of the cylinder will be equal to the volume of 12 spheres.
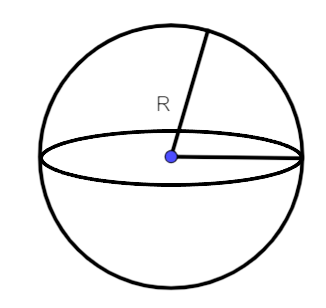
12 Spheres
R=?

Cylinder
Given, $$d = 2\,cm$$
$$h = 16\,cm$$
$$r = \dfrac{2}{2} = 1\,\,cm$$
$$\therefore $$ Volume of 12 spheres = Volume of cylinder
$$ \Rightarrow \,\,\dfrac{4}{3}\pi {R^3} \times 12 = \pi {r^2}h$$
$$ \Rightarrow \,\,16{R^3} = {r^2}h$$
$$ \Rightarrow \,\,{R^3} = \dfrac{{{r^2}h}}{{16}}$$
$$ \Rightarrow \,\,{R^3} = \dfrac{{{{\left( 1 \right)}^2} \times 16}}{{16}}$$
$$ \Rightarrow \,\,{R^3} = 1$$
$$\therefore \,\,\,R = 1\,cm$$
Hence, diameter is $$\left( {2R = 2 \times 1} \right)$$ 2 cm.
13. The radii of the top and bottom of a bucket of slant height 45 cm are 28 cm and 7 cm respectively. The curved surface area of the bucket is
(a) 4950 cm2
(b) 4951 cm2
(c) 4952 cm2
(d) 4953 cm2
Ans: The correct option is (a) 4950 cm2
Given, $${r_1} = 7\,cm$$, $${r_2} = 28\,cm$$ and $$l = 45\,cm$$
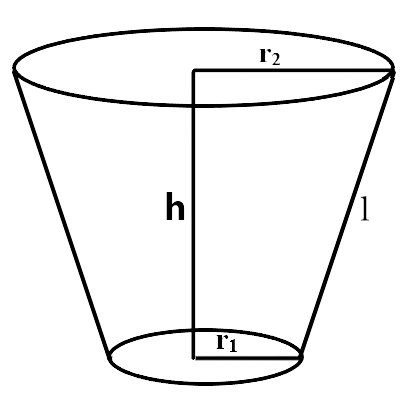
Curved surface area of bucket $$ = \,\,\pi l\left( {{r_1} + {r_2}} \right)$$
$$ \Rightarrow \,\,\,\dfrac{{22}}{7} \times 45\left( {7 + 28} \right)$$
$$ \Rightarrow \,\,\,\dfrac{{22}}{7} \times 45 \times 35$$
$$ \Rightarrow \,\,\,22 \times 45 \times 5$$
$$ \Rightarrow \,\,\,4950\,\,c{m^2}$$
$$\therefore $$ Curved surface area of bucket $$ = \,\,\,4950\,\,c{m^2}$$
14. A medicine-capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each to its ends. The length of the entire capsule is 2 cm. The capacity of the capsule is
(a) 0.36 cm3
(b) 0.35 cm3
(c) 0.34 cm3
(d) 0.33 cm3
Ans: The correct option is (a) 0.36 cm3.
A medicine-capsule consists of 2 Hemisphere and a cylinder
Given, cylinder of diameter $$d = 0.5\,cm$$
$$r = \dfrac{{0.5}}{2} = 0.25\,\,cm$$
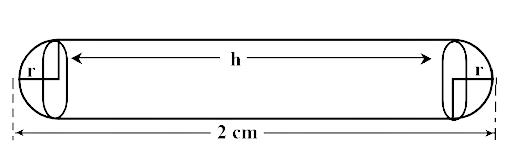
Total length of capsule$$ = r + h + r$$
$$ \Rightarrow \,\,2 = 2r + h$$
$$ \Rightarrow \,\,2 = 2\left( {0.25} \right) + h$$
$$ \Rightarrow \,\,2 = 0.5 + h$$
$$ \Rightarrow \,\,h = 2 - 0.5$$
$$ \Rightarrow \,\,h = 1.5\,\,cm$$
$$\therefore $$ Volume of capsule = Volume of two hemispheres + Volume of cylinder
$$ \Rightarrow \,\,2\left( {\dfrac{4}{3}\pi {r^3} \times \dfrac{1}{2}} \right) + \pi {r^2}h$$
$$ \Rightarrow \,\,\dfrac{4}{3}\pi {r^3} + \pi {r^2}h$$
$$ \Rightarrow \,\,\pi {r^2}\left( {\dfrac{4}{3}r + h} \right)$$
$$ \Rightarrow \,\,\dfrac{{22}}{7} \times {\left( {0.25} \right)^2}\left( {\dfrac{4}{3}\left( {0.25} \right) + 1.5} \right)$$
$$ \Rightarrow \,\,\dfrac{{22}}{7} \times 0.25 \times 0.25\left( {\dfrac{1}{3} + 1.5} \right)$$
$$ \Rightarrow \,\,\dfrac{{22}}{7} \times 0.0625\left( {0.33 + 1.5} \right)$$
$$ \Rightarrow \,\,\dfrac{{22}}{7} \times 0.0625 \times 1.83$$
$$ \Rightarrow \,\,\dfrac{{22}}{7} \times 0.114375$$
$$ \Rightarrow \,\,\dfrac{{2.51625}}{7}$$
$$ \Rightarrow \,\,\,0.3594 \simeq 0.36\,c{m^3}$$
$$\therefore $$ Volume of capsule = 0.36 cm3.
15. If two solid hemispheres of same base radius ‘r’ are joined together along their bases, then curved surface area of this new solid is
(a) $$4\pi {r^2}$$
(b) $$6\pi {r^2}$$
(c) $$3\pi {r^2}$$
(d) $$8\pi {r^2}$$
Ans: The correct option is (a) $$4\pi {r^2}$$
When two hemispheres of equal radii are joined base to base new solid becomes sphere.
$$\therefore $$ Curved surface area of sphere is $$4\pi {r^2}$$.
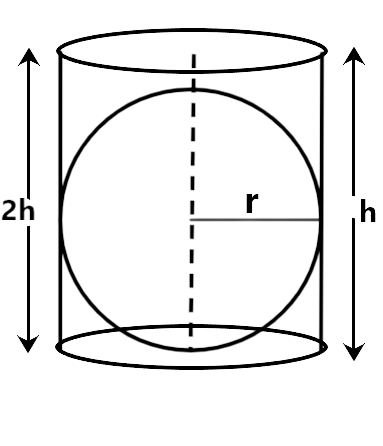
16. A right circular cylinder of radius r cm and height h cm (where h > 2r) just encloses of sphere of diameter
(a) r cm
(b) 2r cm
(c) h cm
(d) 2h cm
Ans: The correct option is (b) 2r cm.
As the cylinder just enclosed the sphere so the radius or diameter of cylinder and sphere are equal.
i.e., 2r and height $$h > 2r$$.
17. During conversion of a solid from one shape to another, the volume of new shape will
(a) increase
(b) decrease
(c) remains unaltered
(d) be doubled
Ans: The correct option is (c) remains unaltered
When a solid is reshaped, the volume of the new solid is equal to the old one or remains unchanged.
18. The diameters of the two circular ends of the bucket are 44 cm and 24 cm. The height of the bucket is 35 cm. The capacity of bucket is:
(a) 32.7 L
(b) 33.7 L
(c) 34.7 L
(d) 37.7 L
Ans: The correct option is (a) 32.7 L.
Given, the diameters of two circular of ends of the bucket are
$${d_1} = 44\,cm$$ and $${d_2} = 24\,cm$$, then
$${r_1} = \dfrac{{{d_1}}}{2} = \dfrac{{44}}{2} = 22\,\,cm$$
$${r_2} = \dfrac{{{d_2}}}{2} = \dfrac{{24}}{2} = 12\,\,cm$$
$$h = 35\,cm$$
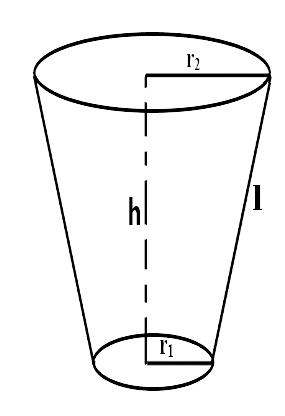
$$\therefore \,$$ The capacity or volume of the bucket $$V = \dfrac{1}{3}\pi h\left( {r_1^2 + r_2^2 + {r_1}{r_2}} \right)$$
$$ \Rightarrow \,\,V = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 35\left( {{{12}^2} + {{22}^2} + 12 \times 22} \right)$$
$$ \Rightarrow \,\,V = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 35\left( {{{12}^2} + {{22}^2} + 12 \times 22} \right)$$
$$ \Rightarrow \,\,V = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 35\left( {144 + 484 + 264} \right)$$
$$ \Rightarrow \,\,V = \dfrac{{1 \times 22 \times 35}}{{3 \times 7}}\left( {892} \right)$$
$$ \Rightarrow \,\,V = \dfrac{{22 \times 5 \times 892}}{3}$$
$$ \Rightarrow \,\,V = \dfrac{{110 \times 892}}{3}\,\,c{m^3}$$
$$ \Rightarrow \,\,V = \dfrac{{110 \times 892}}{{3 \times 1000}}\,\,litre$$
$$ \Rightarrow \,\,V = \dfrac{{11 \times 892}}{{3 \times 100}}\,\,$$
$$ \Rightarrow \,\,V = \dfrac{{9812}}{{300}}\,\,$$
$$\therefore \,\,\,\,V = 32.70\,\,\,$$L
19. In a right circular cone, the cross–section made by a plane parallel to the base is a.
(a) circle
(b) frustum of a cone
(c) sphere
(d) hemisphere
Ans: The correct option is (a) circle.
The cross-section made by a plane parallel to the base will be the same as the base of the cone. As the base of the cone is circular. Hence, we get a circle.
20. Volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
(a) 3 : 4
(b) 4 : 3
(c) 9 : 16
(d) 16 : 9
Ans: The correct option is (d) 16 : 9.
Let us consider $${V_1}$$ and $${V_2}$$ are the volumes of two spheres
$$ \Rightarrow \,\,\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{64}}{{27}}$$
$$ \Rightarrow \,\,\dfrac{{\dfrac{4}{3}\pi r_1^3}}{{\dfrac{4}{3}\pi r_2^3}} = \dfrac{{64}}{{27}}$$
$$ \Rightarrow \,\,\dfrac{{\dfrac{4}{3}\pi r_1^3}}{{\dfrac{4}{3}\pi r_2^3}} = \dfrac{{64}}{{27}}$$
$$ \Rightarrow \,\,\dfrac{{r_1^3}}{{r_2^3}} = \dfrac{{64}}{{27}}$$
$$ \Rightarrow \,\,\dfrac{{r_1^3}}{{r_2^3}} = \dfrac{{{4^3}}}{{{9^3}}}$$
$$ \Rightarrow \,\,{\left( {\dfrac{{{r_1}}}{{{r_2}}}} \right)^3} = {\left( {\dfrac{4}{9}} \right)^3}$$
$$ \Rightarrow \,\,\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{4}{9}$$
Now, the ratio of their surface areas is given by
$$ \Rightarrow \,\,\dfrac{{T.S.{A_1}}}{{T.S.{A_2}}} = \,\,\dfrac{{4\pi r_1^2}}{{4\pi r_2^2}}$$
$$ \Rightarrow \,\,\dfrac{{T.S.{A_1}}}{{T.S.{A_2}}} = \,\,{\left( {\dfrac{{{r_1}}}{{{r_2}}}} \right)^2} = {\left( {\dfrac{4}{3}} \right)^2}$$
$$ \Rightarrow \,\,\dfrac{{T.S.{A_1}}}{{T.S.{A_2}}} = \,\,{\left( {\dfrac{{{r_1}}}{{{r_2}}}} \right)^2} = {\left( {\dfrac{4}{3}} \right)^2}$$
$$ \Rightarrow \,\,\dfrac{{T.S.{A_1}}}{{T.S.{A_2}}} = \,\,\dfrac{{16}}{9}$$
$$\therefore \,\,16:9$$
Short Answer Questions with Reasoning
Write 'True' or 'False' and justify your answer.
Sample Question 1: If a solid cone of base radius r and height h is placed over a solid cylinder having same base radius and height as that of the cone, then the curved surface area of the shape is $$\pi r\sqrt {{h^2} + {r^2}} + 2\pi h$$.
Ans: True.
Since the curved surface area taken is the same as the sum of curved surface areas which is measured separately.
Sample Question 2: A spherical steel ball is melted to make eight new identical balls. Then, the radius of each new ball will be $$\dfrac{1}{8}$$ th the radius of the original ball.
Ans: False.
Let r be the radius of the original steel ball and $${r_1}$$ be the radius of the newly formed ball after melting.
Therefore, $$\dfrac{4}{3}\pi {r^3} = 8 \times \dfrac{4}{3}\pi r_1^3$$
$$ \Rightarrow {r_1} = \dfrac{r}{2}$$
Sample Question 3: Two identical solid cubes of side a are joined end to end. Then the total surface area of the resulting cuboid is $$12{a^2}$$
Ans: False.
The total surface area of a cube with side a is $$6{a^2}$$. If two identical faces of side a are joined together, then the total surface area of the cuboid so formed will be equal to $$10{a^2}$$.
Sample Question 4: Total surface area of a lattu (top) as shown in the Figure is the sum of total surface area of hemisphere and the total surface area of cone.

Total surface area of the lattu is the sum of curved surface area of hemisphere and curved surface area of the cone.
Sample Question 5: Actual capacity of a vessel as shown in the Figure is equal to the difference of volume of the cylinder and volume of the hemisphere.

Actual capacity of the vessel is the empty space inside the glass that can accommodate something when poured into it.
Exercise 12.2
Write ‘True’ or ‘False’ and justify your answer in the following:
1. Two identical solid hemispheres of equal base radius r cm are stuck together along their bases. The total surface area of the combination is $$16\pi {r^2}$$
Ans: False.
When two identical solid hemispheres with equal bases are placed base to base, a sphere is formed, and we know that the sphere's total surface area is $$4\pi {r^2}$$.
$$\therefore $$ The given statement is false.
2. A solid cylinder of radius r and height h is placed over another cylinder of same height and radius. The total surface area of the shape so formed is $$4\pi rh + 4\pi {r^2}$$.
Ans: False, When two identical cylinders of same radius ‘r’ and height ‘h’ are stuck base to base (circular), then the resulting cylinder will have height $$h' = 2h$$ and radius $$r' = r$$.
$$\therefore \,\,\,T.S.A. = 2\pi r'\left( {r' + h'} \right)$$
$$ \Rightarrow \,\,\,T.S.A = 2\pi r\left( {r + 2h} \right)$$
$$ \Rightarrow \,\,\,T.S.A = 2\pi {r^2} + 2\pi r \cdot 2h$$
$$\therefore \,\,\,T.S.A = 2\pi {r^2} + 4\pi rh$$
$$\therefore $$ The given statement is false.
3. A solid cone of radius r and height h is placed over a solid cylinder having the same base radius and height as that of a cone. The total surface area of the combined solid is $$\pi r\left[ {\sqrt {{r^2} + {h^2}} + 3r + 2h} \right]$$.
Ans: False.
Given a solid cone and solid cylinder having the same radius ‘r’ and height ‘h’. Then,
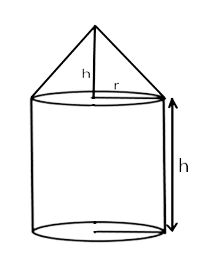
$$\therefore $$ Total surface area of combined solid
= Curved surface area of cone + Curved surface area of cylinder + Area of the base of cylinder
$$ \Rightarrow \,\,\pi rl + 2\pi rh + \pi {r^2}$$
$$ \Rightarrow \,\,\pi r[l + 2h + r]$$
But, $$l = \sqrt {{r^2} + {h^2}} $$
$$\therefore $$ Total surface area of combined solid $$ = \pi r\left[ {\sqrt {{r^2} + {h^2}} + 2r + r} \right]$$.
Hence, the given statement is false.
4. A solid ball is exactly fitted inside the cubical box of side a. The volume of the ball is $$\dfrac{4}{3}\pi {a^3}$$.
Ans: False, when a spherical ball is exactly fitted inside the cubical box then diameter of the ball becomes equal to side of cube so, then
Diameter = d = a
$$ \Rightarrow $$ Radius $$ = r = \dfrac{a}{2}$$
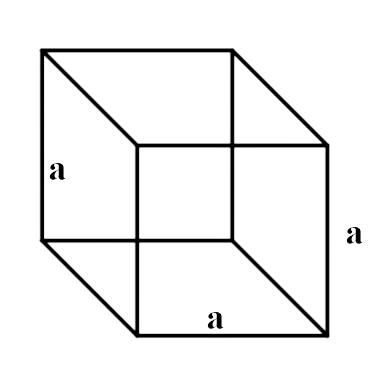
$$\therefore $$ Volume of spherical ball $$ = \dfrac{4}{3}\pi {r^3}$$
$$ \Rightarrow \,\,\dfrac{4}{3}\pi {\left( {\dfrac{a}{2}} \right)^3}$$
$$ \Rightarrow \,\,\dfrac{4}{3}\pi \dfrac{{{a^3}}}{8}$$
$$ \Rightarrow \,\,\dfrac{1}{6}\pi {a^3}$$
$$\therefore $$ Volume of spherical ball$$ = \,\,\dfrac{1}{6}\pi {a^3}$$
Hence, the given statement is false.
5.The volume of the frustum of cone is $$\dfrac{1}{3}\pi h\left[ {r_1^2 + r_2^2 - {r_1}{r_2}} \right]$$, where h is the vertical height of the frustum and $${r_1}$$, $${r_2}$$ are the radii of the ends.
Ans: False.
As we know that the volume of frustum cone $$V = \dfrac{1}{3}\pi h\left[ {r_1^2 + r_2^2 + {r_1}{r_2}} \right]$$.
Hence, the given statement is false.
6.The capacity of a cylindrical vessel with a hemispherical portion raised upward, at the bottom as shown in figure is $$\dfrac{{\pi {r^2}}}{3}\left( {3h - 2r} \right)$$.
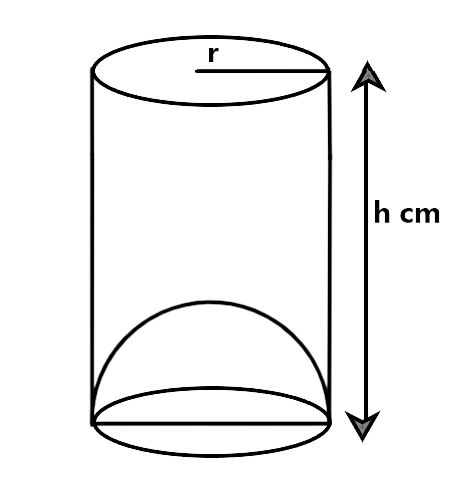
Ans: True,
By the figure, the radius of the cylinder and hemisphere is ‘r’ cm and height of the cylinder ‘h’ cm.
$$\therefore $$ Capacity of vessel = Volume of cylinder – Volume of hemisphere
$$ \Rightarrow \,\,\pi {r^2}h - \dfrac{2}{3}\pi {r^3}$$
$$\therefore $$ Capacity of vessel = $$\dfrac{{\pi {r^2}}}{3}\left( {3h - 2r} \right)$$.
Hence, the given statement is true.
7. The curved surface area of a frustum of a cone is $$\pi l({r_1} + {\text{ }}{r_2})$$, where $$l = \sqrt {{h^2} + {{\left( {{r_1} + {r_2}} \right)}^2}} $$, $${r_1}$$, $${r_2}$$ are the radii of the two ends of frustum and h is vertical height.
Ans: False.
We know that the curved surface area of a frustum of a cone $$ = \pi l({r_1} + {\text{ }}{r_2})$$
But, $$l = \sqrt {{h^2} + {{\left( {{r_1} - {r_2}} \right)}^2}} $$
Hence, the given statement is false.
8. An open metallic bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The surface area of the metallic sheet used is equal to the curved surface area of frustum of a cone + area of circular base + curved surface area of cylinder.
Ans: True, The total surface area of the cylinder excluding the top and just the curved surface area of the frustum of a cone will be equal to the surface area of the sheet used for the vessel.
$$\therefore $$ Total surface area of vessel
= Curved surface area of frustum + Curved surface area of cylinder + Area of base cylinder.
It is equal to the surface area of the metallic sheet.
Hence, the given statement is true.
Short Answer Questions
Sample Question 1: A cone of maximum size is carved out from a cube of edge 14 cm. Find the surface area of the cone and of the remaining solid left out after the cone is carved out.
Ans: The cone of maximum size that is carved out from a cube of edge = 14 cm, base radius = 7 cm and height = 14 cm.
Surface area of the cone = $$\pi rl + \pi {r^2}$$
$$ = \dfrac{{22}}{7} \times 7 \times \sqrt {{7^2} + {{14}^2}} + \dfrac{{22}}{7}{(7)^2}$$
$$ = 154\sqrt 5 + 154\,\,c{m^2}$$
$$ = 154(\sqrt 5 + 1)\,\,c{m^2}$$
Surface area of the cube $$ = 6 \times {14^2} = 1176\,\,c{m^2}$$
So, surface area of the remaining solid left out after the cone is carved out $$ = (1176 - 154 + 154\sqrt 5 )\,\,c{m^2}$$
$$ = 1022 + 154\sqrt 5 \,\,c{m^2}$$
Sample Question 2: A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
Ans: The volume of solid metallic sphere $$ = \dfrac{4}{3}\pi {(10.5)^3}\,\,c{m^3}$$
Volume of a cone of radius 3.5 cm and of height 3 cm $$ = \dfrac{1}{3}\pi {(3.5)^2} \times 3\,\,c{m^3}$$
Number of cones so formed $$ = \dfrac{{\dfrac{4}{3}\pi {{(10.5)}^3}\,}}{{\dfrac{1}{3}\pi {{(3.5)}^2} \times 3\,\,}} = 126$$
Sample Question 3: A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing at a speed of 20 km per hour. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired?
Ans: Volume of water flows in the canal in one hour is equal to product of width of the canal , depth of the canal and speed of the canal water $$ = 3 \times 1.2 \times 20 \times 1000 = 72000\,{m^3}$$
In 20 minutes the volume of water $$ = \dfrac{{72000 \times 20}}{{60}} = 24000\,{m^3}$$
The Area irrigated in 20 minutes, if 8 cm , i.e., 0.08 m standing water is required $$ = \dfrac{{24000}}{{0.08}} = 300000\,{m^2}$$= 30 hectares
Sample Question 4: A cone of radius 4 cm is divided into two parts by drawing a plane through the midpoint of its axis and parallel to its base. Compare the volumes of the two parts.
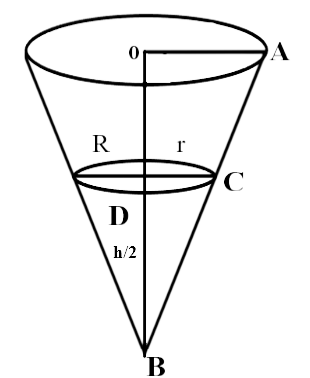
Ans: Let h be the height of the given cone. On dividing the cone along the mid-point of its axis and parallel to its base into two parts, we obtain the following figure.
The triangle OAB and DCB are similar triangles by AA similarity.
$$\dfrac{{OA}}{{CD}} = \dfrac{{OB}}{{BD}}$$
$$ \Rightarrow \dfrac{4}{r} = \dfrac{h}{{\dfrac{h}{2}}}$$
$$ \Rightarrow r = 2$$
Therefore, $$ =\dfrac{{Volume\,\,of\,\,smaller\,\,cone}}{{Volume\,\,of\,\,frustum\,\,of\,\,cone}} = \dfrac{{\dfrac{1}{3}\pi {{(2)}^2}\left( {\dfrac{h}{2}} \right)}}{{\dfrac{1}{3}\pi \left( {\dfrac{h}{2}} \right)[{4^2} + {2^2} + 4 \times 2]}} = \dfrac{1}{7}$$
Therefore, the ratio of volume of smaller cone to the volume of frustum of cone is 1:7
Sample Question 5: Three cubes of a metal whose edges are in the ratio 3:4:5 are melted and converted into a single cube whose diagonal is $$12\sqrt 3 $$cm. Find the edges of the three cubes.
Ans: Let the edges of three cubes (in cm ) be 3x, 4x and 5x respectively.
Volume of the cubes after melting is $$ = {(3x)^3} + {(4x)^3} + {(5x)^3} = 216\,c{m^3}$$
Let a be the side of the new cube which has formed after melting.
Therefore, $${a^3} = 216{x^3}$$
So, a = 6x,
Diagonal $$ = \sqrt {{a^2} + {a^2} + {a^2}} = a\sqrt 3 $$
But it is given that the diagonal of the new cube is $$12\sqrt 3 $$cm. Therefore, $$a\sqrt 3 = 12\sqrt 3 $$, i.e., a=12.
This gives x = 2 Therefore, edges of the three cubes are 6 cm , 8 cm and 10 cm respectively.
EXERCISE 12.3
1. Three metallic solid cubes whose edges are 3 cm, 4 cm and 5 cm are melted and formed into a single cube. Find the edges of the cube so formed.
Ans: Volume of new cube is equal to the sum of volumes of three cubes in the recasting process. The edge of the first cube is 3cm, the edge of the second cube is 4 cm and the edge of the third cube is 5cm.
$$V = {V_1} + {V_2} + {V_3}$$
$$ \Rightarrow {a^3} = a_1^3 + a_2^3 + a_3^3$$
$$ \Rightarrow {a^3} = {3^3} + {4^3} + {5^3}$$
$$ \Rightarrow {a^3} = 27 + 64 + 125$$
$$ \Rightarrow {a^3} = 216$$
$$ \Rightarrow a = 6\,$$
Hence, the edge of the new cube is 6 cm.
2. How many shots each having diameter 3 cm, can be made from a cuboidal lead solid of dimensions $$9cm \times 11cm \times 12cm$$ ?
Ans: Let n represent the number of spherical shots. The length, breadth and height of the cuboidal lead solid is 12 cm, 11 cm and 9 cm respectively. The radius of spherical shots is $$r = \dfrac{3}{2}\,\,cm = 1.5\,\,cm$$
Lead cuboid is recasted into lead spherical shots. So,
Volume of n spherical shots = Vol. of cuboid.
$$ \Rightarrow n.\dfrac{4}{3}\pi {r^3} = lbh$$
$$ \Rightarrow n \times \dfrac{4}{3} \times \dfrac{{22}}{7} \times 1.5 \times 1.5 \times 1.5 = 12 \times 11 \times 9$$
$$ \Rightarrow n = \dfrac{{12 \times 11 \times 9 \times 3 \times 7}}{{4 \times 22 \times 1.5 \times 1.5 \times 1.5}}$$
$$ \Rightarrow n = 84$$
Hence, 84 lead shots can be made.
3. A bucket is in the shape of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28 cm and 21 cm respectively. Find the height of the bucket.
Ans: The lower and upper radius of the frustum of a cone is given as $${r_1} = 21\,cm$$ and $${r_2} = 28\,cm$$. The volume V=28.490 L = $$28.490 \times 1000c{m^3} = 28490\,c{m^3}$$
$$V = \dfrac{1}{3}\pi h\left[ {r_1^2 + r_2^2 + {r_1}{r_2}} \right]$$
$$ \Rightarrow 28490 = \dfrac{1}{3} \times \dfrac{{22}}{7} \times h\left[ {{{(21)}^2} + {{(28)}^2} + (21)(28)} \right]$$
$$ \Rightarrow 28490 = \dfrac{1}{3} \times \dfrac{{22}}{7} \times h\left[ {441 + 784 + 588} \right]$$
$$ \Rightarrow 28490 = \dfrac{1}{3} \times \dfrac{{22}}{7} \times h\left[ {1813} \right]$$
$$ \Rightarrow h = \dfrac{{28490 \times 3 \times 7}}{{22 \times 1813}}$$
$$ \Rightarrow h = 15$$
Hence, the height of the bucket = 15 cm
4. A cone of radius 8 cm and height 12 cm is divided into two parts by a plane through the mid-point of its axis parallel to its base. Find the ratio of the volumes of two parts.
Ans: The radius and height of the cone is $${r_2} = 8\,cm$$ and height is $$h = 12\,cm$$. When the cone is divided into two equal parts then the radius of the cone is $${r_1} = 4\,cm$$ and height is $${h_1} = 6\,cm$$. The lower radius and upper radius is $${r_1} = 4\,cm$$and $${r_2} = 8\,cm$$of frustum and height is $${h_2} = 6\,cm$$
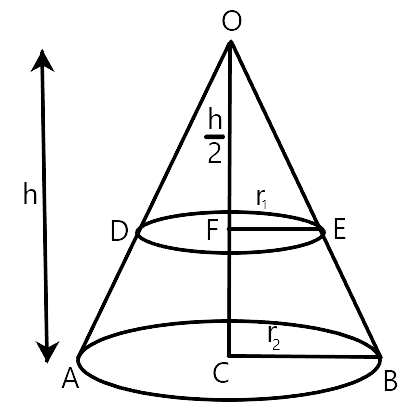
$$\vartriangle OEF \sim \vartriangle OBC$$[By AA criterion of similarity]
$$\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{{{h_1}}}{{{h_2}}} \Rightarrow \dfrac{{{r_1}}}{8} = \dfrac{{\dfrac{h}{2}}}{h} = \dfrac{1}{2}$$
$$ \Rightarrow {r_1} = 4\,cm$$
$$\dfrac{{Vol.\,\,of\,\,frustum\,\,(DEBA)}}{{Vol.\,\,of\,cone\,(ODE)}} = \dfrac{{\dfrac{1}{3}\pi {h_2}\left[ {r_1^2 + r_2^2 + {r_1}{r_2}} \right]}}{{\dfrac{1}{3}\pi r_1^2{h_1}}}$$.
$$ = \dfrac{{6\left[ {{4^2} + {8^2} + 4 \times 8} \right]}}{{4 \times 4 \times 6}} = \dfrac{{6\left[ {112} \right]}}{{96}} = \dfrac{7}{1}$$
Volume of frustum: Volume of smaller cone = 7:1
5. Two identical cubes each of volume 64$$c{m^3}$$ are joined together end to end. What is the surface area of the resulting cuboid?
Ans: Two identical cubes of side a are joined end to end to form a cuboid. Let length, breadth and height of cuboid is 2a units, a units and a units respectively.
So, the surface area of the resulting cuboid is
$$ = 2\left[ {lb + bh + hl} \right]$$
$$ = 2\left[ {2a.a + 2a.a + a.a} \right]$$
$$ = 10{a^2}...\left( i \right)$$
Volume of the cube $$ = 64\,\,c{m^3}$$
$$ \Rightarrow {a^3} = {(4)^3}$$
$$ \Rightarrow a = 4\,\,cm$$
Total surface area of cuboid$$ = 10 \times 4 \times 4$$ [From (i)]
Hence, the required surface area $$ = 160\,\,c{m^2}$$
6. From a solid cube of side 7cm , a conical cavity of height 7 cm and radius 3cm is hollowed out. Find the volume of remaining solid.
Ans: The radius and height of the cube is 3 cm and 7 cm respectively. The side of the cube is 7 cm.
Vol. of remaining solid = Vol. of cube - Vol. of cone
$$ = {a^3} - \dfrac{1}{3}\pi {r^2}h$$
$$ = {(7)^3} - \dfrac{1}{3} \times \dfrac{{22}}{7} \times {(3)^2} \times 7$$
$$ = 343 - 66 = 277\,\,c{m^3}$$
Hence, the volume of remaining solid $$ = 277\,\,c{m^3}$$
7. Two cones with the same base radius 8cm and height 15cm are joined together along their bases. Find the surface area of the shape so formed.
Ans: When two identical cones are joined base to base, then the total surface area of the new solid becomes equal to the sum of curved surface areas of both the cones.
So, the total surface area of solid $$ = \pi rl + \pi rl = 2\pi rl$$
In two cones, r = 8cm, h = 15cm
By the Pythagoras theorem $${l^2} = {r^2} + {h^2} = {8^2} + {15^2} = 64 + 225 = 289$$
$$ \Rightarrow {l^2} = {(17)^2}$$
$$ \Rightarrow l = 17\,\,cm$$
Total surface area of solid $$ = 2\pi rl$$
$$ = 2 \times \pi \times 8 \times 17 = 272\pi c{m^2} = 854.857c{m^2}$$
Hence, the surface area of new solid $$ = 854.857c{m^2}$$.
8. Two solid cones A and B placed in a cylindrical tube as shown in the figure. The ratio of their capacities is 2:1. Find the heights and capacities of cones. Also, find the volume of the remaining portion of the cylinder.
Ans: As the ratio of volumes of cone $${C_1}$$ and $${C_2}$$ is 2:1, their radii are same and is equal to $$r = \dfrac{6}{2} = 3\,cm$$
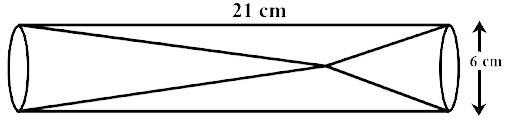
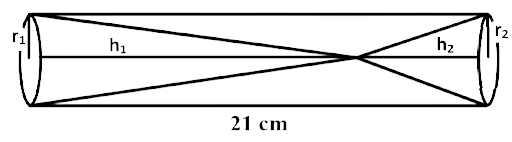
$$\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\dfrac{1}{3}\pi r_1^2{h_1}}}{{\dfrac{1}{3}\pi r_2^2{h_2}}}$$
$$ \Rightarrow \dfrac{2}{1} = \dfrac{{{3^2}{h_1}}}{{{3^2}{h_2}}}$$
$$ \Rightarrow {h_1} = 2{h_2}...(i)$$
Also, $${h_1} + {h_2} = 21\,cm$$
$$ \Rightarrow 2{h_2} + {h_2} = 21$$ [using (i)]
$$ \Rightarrow 3{h_2} = 21$$
$$ \Rightarrow {h_2} = 7\,\,cm$$
Now, $${h_1} = 21 - 7 = 14\,cm$$...(ii)
Hence, the height of $${C_1}$$ is 14cm and height of $${C_2}$$ is 7cm. The radius and height of $${C_1}$$ is 3 cm and 14 cm respectively. The radius and height of $${C_2}$$ is 3 cm and 7 cm respectively. The radius and height of the cylinder is 3 cm and 21 cm respectively.
Volume of cone $${C_1}$$$$ = \dfrac{1}{3}\pi r_1^2{h_1} = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 3 \times 3 \times 14 = 132\,c{m^2}$$
Volume of cone $${C_2}$$$$ = \dfrac{1}{3}\pi r_2^2{h_2} = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 3 \times 3 \times 7 = 66\,c{m^2}$$
Volume of remaining portion of tube = Vol. of cylinder - Vol. of cone $${C_1}$$- Vol. of cone $${C_2}$$
$$ = \pi {r^2}h - 132 - 66$$
$$ = \dfrac{{22}}{7} \times 3 \times 3 \times 21 - 198$$
$$ = 594 - 198 = 396\,\,c{m^2}$$
Hence, the required volume is $$396\,\,c{m^2}$$
9. An ice-cream cone full of ice-cream having radius 5cm, and height 10cm, as shown in figure. Calculate the volume of ice-cream, provided that its $$\dfrac{1}{6}$$ part is left unfilled with ice-cream.
Ans: Ice-cream cones can be considered as a hemisphere surmounted on a cone.
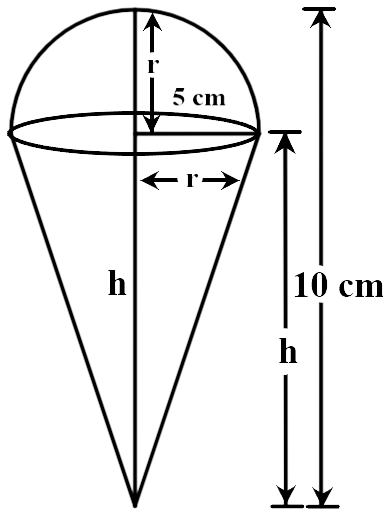
The radius of the hemisphere is 5 cm. The radius and height of the cone is 5 cm and 5 cm respectively. The $$\dfrac{1}{6}$$ part of ice-cream is left unfilled.
So, Vol. of ice-cream= $$\left( {1 - \dfrac{1}{6}} \right)$$ (Sum of the Volumes of cone and hemisphere)
$$ = \dfrac{5}{6}\left[ {\dfrac{1}{3}\pi {r^2}h + \dfrac{2}{3}\pi {r^3}} \right] = \dfrac{5}{6} \times \dfrac{1}{3}\pi {r^2}\left[ {h + 2r} \right]$$
$$ = \dfrac{{5 \times 22 \times 5 \times 5}}{{6 \times 3 \times 7}}\left[ {5 + 2 \times 5} \right]$$
$$ = \dfrac{{6875}}{{21}} \cong 327.4\,\,c{m^3}$$
Hence, the volume of ice-cream in cone is $$327.4\,\,c{m^3}$$
10. Marbles of diameter 1.4cm are dropped into a cylindrical beaker of diameter 7cm, containing some water. Find the number of marbles that should be dropped into the beaker so that water level rises by 5.6cm.
Ans: When n marbles are dropped into the cylindrical beaker which is filled partially with water, the volume of water raised in the beaker, will be equal to the volume of n marbles, The shape of water raised in the beaker is cylindrical.
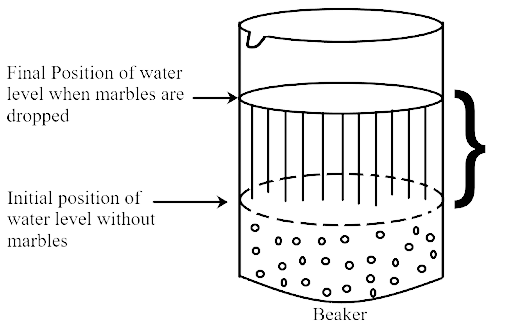
The radius and height of the cylindrical beaker is r = 3.5 cm and h = 5.6 cm respectively. The radius of spherical marbles R = 0.7 cm
Final position of water level when marbles are dropped is
Vol. of n spherical balls = Vol. of water raised in cylinder
$$ \Rightarrow n \times \dfrac{4}{3}\pi {R^3} = \pi {r^2}h$$
$$ \Rightarrow n \times \dfrac{4}{3} \times 0.7 \times 0.7 \times 0.7 = 3.5 \times 3.5 \times 5.6$$
$$ \Rightarrow n = \dfrac{{3.5 \times 3.5 \times 5.6 \times 3}}{{0.7 \times 0.7 \times 0.7 \times 4}}$$
$$ \Rightarrow n = 150$$
Hence, required number of marbles = 150
11. How many spherical lead shots each of diameter 4.2cm can be obtained from a solid rectangular lead piece with dimensions 66cm, 42cm and 21cm?
Ans: Let n spherical shots can be obtained. The radius of spherical shots is $$r = \dfrac{{4.2}}{2} = 2.1\,\,cm$$
The length, breadth and height of the cuboid is 66 cm, 42 cm and 21 cm.
Volume of n spherical lead shots = Vol. of lead cuboid
$$ \Rightarrow n \times \dfrac{4}{3}\pi {r^3} = lbh$$
$$ \Rightarrow n \times \dfrac{4}{3} \times \dfrac{{22}}{7} \times 2.1 \times 2.1 \times 2.1 = 66 \times 42 \times 21$$
$$ \Rightarrow n = \dfrac{{66 \times 42 \times 21 \times 7 \times 3}}{{4 \times 22 \times 2.1 \times 2.1 \times 2.1}}$$
$$ \Rightarrow n = 1500$$
Hence, the number of lead shots are = 1500
12. How many spherical lead shots of diameter 4cm can be made out of a solid cube of lead whose edge measures 44cm?
Ans: Let we consider spherical shots can be made out as n. The edge of the cube is 44 cm. The radius of the spherical shots $$r = \dfrac{4}{2} = 2\,cm$$.
Solid cube is recasted into n spherical lead shots.
Therefore Vol. of n spherical lead shots = Vol. of cube
$$ \Rightarrow n.\dfrac{4}{3}\pi {r^3} = {a^3}$$
$$ \Rightarrow n \times \dfrac{4}{3} \times \dfrac{{22}}{7} \times 2 \times 2 \times 2 = {(44)^3}$$
$\Rightarrow n = \dfrac{{44 \times 44 \times 44 \times 3 \times 7}}{{4 \times 22 \times 2 \times 2 \times 2}} $
$ \Rightarrow n = 2541 $
Hence, the number of lead shots are 2541.
13. A wall 24 m long, 0.4 m thick and 6m high is constructed with the bricks each of dimensions $$25cm \times 16cm \times 10cm$$. If the mortar occupies $$\dfrac{1}{{10}}$$ th of the volume of the wall, then find the number of bricks used in constructing the wall.
Ans: The length of the wall is 24m, breadth is 04.m and height is 6m.
So, volume of wall $$ = 24m \times 0.4m \times 6m$$
Since $$\dfrac{1}{{10}}$$ th of the volume of the wall is occupied by mortar, so the volume of bricks in the wall $$ = \left( {1 - \dfrac{1}{{10}}} \right)$$ part of the wall.
=$$\left( {\dfrac{9}{{10}}} \right)$$th part of the wall
$$ = \dfrac{9}{{10}} \times 57.6 = 51.84\,{m^3}$$
Volume of one brick $$ = 25 \times 16 \times 10 = 4000\,c{m^3}$$
$$ = 0.004\,\,{m^3}$$
Required number of bricks $$ = \dfrac{\text{Vol.of bricks in the wall}}{\text{Vol. of one brick}} = \dfrac{{51.84}}{{0.004}} = 12960$$
So, 12960 bricks are used in constructing the wall.
14. Find the number of metallic circular discs with 1.5cm base diameter and of height 0.2cm to be melted to form a right circular cylinder of height 10cm and diameter 4.5cm.
Ans: The radius and height of the circular disc is 0.75 cm and 0.2 cm respectively. The radius and height of the circular cylinder is 2.25 cm and 10 cm respectively.
Required number of metallic discs $$ = \dfrac{\text{Vol. of right circular cylinder}}{\text{Vol. of one metallic circular disc}} = \dfrac{{\pi {{(2.25)}^2} \times 10}}{{\pi {{(0.75)}^2} \times 0.2}} = 450$$
Long Answer Questions
Sample Question 1: A bucket is in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm, respectively. Find the capacity and surface area of the bucket. Also, find the cost of milk which can completely fill the container, at the rate of Rs 25 per liter ( use $$\pi = 3.14$$)
Ans:
(Image will be uploaded soon)
Volume or Capacity of the bucket $$ = \dfrac{{\pi h}}{3}\left[ {r_1^2 + r_2^2 + {r_1}{r_2}} \right]$$
Given, $$h = 30\,cm$$, $${r_1} = 20\,cm$$ and $${r_2} = 10\,cm$$.
$$\therefore $$ Capacity of bucket $$ = \dfrac{{3.14 \times 30}}{3}\left[ {{{20}^2} + {{10}^2} + 20 \times 10} \right]\,\,c{m^3}$$
$$ \Rightarrow 31.4\left[ {400 + 100 + 200} \right]\,\,c{m^3}$$
$$ \Rightarrow 31.4\left[ {700} \right]\,\,c{m^3}$$
$$ \Rightarrow 21980\,\,c{m^3} = 21.980\,litres$$
$$\therefore $$ Capacity of bucket$$ = 21.980\,litres$$
Given, cost of 1 liter of milk = Rs 25
Cost of 21.980 liters of milk $$ = 21.980\, \times 25 = Rs\,\,549.50$$
Surface area of the bucket = curved surface area of the bucket + surface area of the bottom
$$ \Rightarrow \,\,\pi l\left( {{r_1} + {r_2}} \right) + \pi r_2^2$$
where, $$l = \sqrt {{h^2} + {{\left( {{r_1} - {r_2}} \right)}^2}} = \sqrt {{{30}^2} + {{\left( {20 - 10} \right)}^2}} = \sqrt {900 + 100} = \sqrt {1000} = 31.62\,cm$$
$$\therefore $$ Surface area of the bucket $$ = \,\,3.14 \times 31.62\left( {20 + 10} \right) + 3.14{\left( {10} \right)^2}$$
$$ \Rightarrow \,\,\,3.14\left[ {948.6 + 100} \right]$$
$$ \Rightarrow \,\,\,3.14\left[ {1048.6} \right]$$
$$ \Rightarrow \,\,\,3292.6\,c{m^2}$$
$$\therefore $$ Surface area of the bucket $$ = \,\,\,3292.6\,\,c{m^2}$$ (approx.)
Sample Question 2 : A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 4 cm and the diameter of the base is 8 cm. Determine the volume of the toy. If a cube circumscribes the toy, then find the difference of the volumes of the cube and the toy. Also, find the total surface area of the toy.
Ans: Given, diameter of base $$d = 8\,cm$$
But, $$r = \dfrac{d}{2} = \dfrac{8}{2} = 4\,cm$$
Let ‘$$r$$’ be the radius of the hemisphere and the cone and $$h = 4\,cm$$ be the height of the cone. Then
Volume of the toy = Volume of the hemisphere + Volume of the cone
$$ \Rightarrow \,\dfrac{2}{3}\pi {r^3} + \dfrac{1}{3}\pi {r^2}h$$
$$ \Rightarrow \,\left( {\dfrac{2}{3} \times \dfrac{{22}}{7} \times {4^3} + \dfrac{1}{3} \times \dfrac{{22}}{7} \times {4^2} \times 4} \right)$$
$$ \Rightarrow \dfrac{{1048}}{7}$$ $$c{m^3}$$
$$\therefore $$ Volume of the toy $$ = \dfrac{{1048}}{7}$$ $$c{m^3}$$
A cube circumscribes the given solid. Therefore, the edge of the cube should be 8 cm.
Volume of the cube$$ = {8^3} = 512\,c{m^3}$$
Difference in the volumes of the cube and the toy $$ = \left( {512\, - \dfrac{{1408}}{7}} \right) = 310.86\,\,c{m^3}$$
Total surface area of the toy = Curved surface area of cone + curved surface area of hemisphere
$$ \Rightarrow \,\,\,\pi rl + 2\pi {r^2}$$, where $$l = \sqrt {{h^2} + {r^2}} $$
$$ \Rightarrow \,\,\pi r\left( {l + 2r} \right)$$
$$ \Rightarrow \,\,\dfrac{{22}}{7} \times 4\left( {\sqrt {{4^2} + {4^2}} + 2\left( 4 \right)} \right)$$
$$ \Rightarrow \,\,\dfrac{{88}}{7}\left( {4\sqrt 2 + 8} \right)$$
$$ \Rightarrow \,\,\dfrac{{88}}{7}\left( {13.65} \right)$$
$$ \Rightarrow \,\,171.68\,\,c{m^2}$$
$$\therefore $$ Total surface area of the toy $$ = \,\,171.68\,\,c{m^2}$$
Sample Question 3: A building is in the form of a cylinder surmounted by a hemispherical dome. The base diameter of the dome is equal to $$\dfrac{2}{3}$$ of the total height of $$H = h - \dfrac{h}{3} = \dfrac{{2h}}{3}$$ of air.

Ans: Let the radius of the hemispherical dome be r metres and total height of the building be h metres.
Since the base diameter of the dome is equal to $$\dfrac{2}{3}$$ of the total height, therefore $$2r = \dfrac{2}{3}h$$ $$ \Rightarrow r = \dfrac{h}{3}$$.
Let H metres be the height of the cylindrical portion. Therefore, $$H = h - \dfrac{h}{3} = \dfrac{{2h}}{3}$$metres.
Volume of the air inside the building = Volume of air inside the dome + Volume of the air inside the cylinder
$$ = \dfrac{2}{3}\pi {r^3} + \pi {r^2}H$$, where H is the height of the cylindrical portion
$$ = \dfrac{2}{3}\pi {\dfrac{h}{3}^3} + \pi {\dfrac{h}{3}^2}\dfrac{2}{3}h = \dfrac{8}{{81}}\pi {h^3}$$ cubic metres.
Volume of the air inside the building is $$67\dfrac{1}{{21}}{m^3}$$
Therefore,$$\dfrac{8}{{81}}\pi {h^3} = \dfrac{{1408}}{{21}}$$
h= 6m.
EXERCISE 12.4
1. A solid metallic hemisphere of radius 8cm is melted and recasted into a right circular cone of base radius 6 cm. Determine the height of the cone.
Ans: The radius of hemisphere is given by $$R = 8cm$$
The radius of cone is given by $$r = 6\,cm$$
As the hemisphere is recasted into a cone. So,
Volume of cone = Volume of hemisphere
$$ \Rightarrow \dfrac{1}{3}\pi {r^2}h = \dfrac{2}{3}\pi {R^3}$$
$$ \Rightarrow {r^2}h = 2{R^3}$$
$$ \Rightarrow h = \dfrac{{2{R^3}}}{{{r^2}}} = \dfrac{{2 \times 8 \times 8 \times 8}}{{6 \times 6}} = \dfrac{{256}}{9}$$
$$ \Rightarrow h = 28.44\,cm$$
Hence, the height of the cone is 28.4 cm.
2. A rectangular water tank of base $$11\,m \times 6\,m$$ contains water upto a height of 5m. If the water in the tank is transferred to a cylindrical tank of radius 3.5 cm, find the height of the water level in the tank.
Ans: The schematic representation of rectangular water tank and cylindrical tank is given as follows:
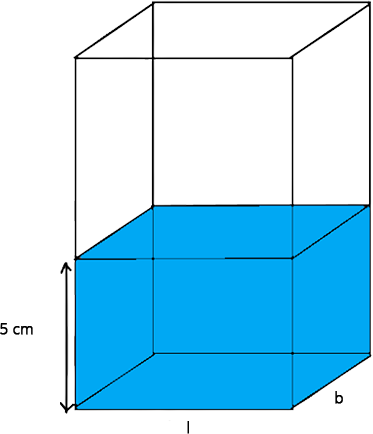
Water is transferred from cuboid to cylinder, so the volume of water in both vessels will be the same.
$$\therefore {\pi ^2}h = l \times b \times H$$
$$ \Rightarrow \dfrac{{22}}{7} \times 3.5 \times 3.5 \times h = 11 \times 6 \times 5$$
$$ \Rightarrow h = \dfrac{{11 \times 6 \times 5 \times 7 \times 100}}{{22 \times 35 \times 35}} = \dfrac{{60}}{7}$$
$$ \Rightarrow h = 8.6\,m\,(approx.)$$
Hence, the height of the water level in the cylindrical tank is 8.6 m.
3. How many cubic centimetres of iron is required to construct an open box whose external dimensions are 36 cm, 25 cm and 16.5 cm provided the thickness of the iron is 1.5 cm. If one cubic centimeter of iron weighs 7.5 g, find the weight of the box.
Ans: The external dimensions and internal dimensions of an open box is given in the table given below:
External dimensions | Internal dimensions |
$${l_2} = 36\,cm$$ | $${l_1} = 36 - 1.5 - 1.5 = 33\,cm$$ |
$${b_2} = 25\,cm$$ | $${b_1} = 25 - 1.5 - 1.5 = 22\,cm$$ |
$${h_2} = 16.5\,cm$$ | $${h_1} = 16.5 - 1.5 = 15\,cm$$ |
Volume of iron in the open box $$ = {l_2}{b_2}{h_2} - {l_1}{b_1}{h_1}$$
$$ = (36 \times 25 \times 16.5) - (33 \times 22 \times 15)$$
$$ = 14850 - 10890$$
$$ = 3960\,c{m^3}$$
Volume of iron is $$3960\,c{m^3}$$
$$1\,c{m^3}$$ of iron weighs = 7.5 gm
So, $$3960\,c{m^3}$$of iron will weight $$ = \dfrac{{3960 \times 75}}{{10}} = 396 \times 75\,gm$$
$$ = \dfrac{{396 \times 75}}{{1000}}\,kg = \dfrac{{297}}{{10}}\,kg$$
Hence, the weight of the box = 29.7 kg
4. The barrel of a fountain pen, cylindrical in shape, is 7cm long and 5mm in diameter. A full barrel of ink in the pen is used up on writing 3300 words on an average. How many words can be written in a bottle of ink containing one-fifth of a litre ?
Ans: Let, n times the barrel of pen is filled.
Radius of barrel,$$r = \dfrac{{5\,mm}}{2} = \dfrac{5}{{20}}\,cm = \dfrac{1}{4}\,cm$$
Height of barrel, h = 7 cm
$$\therefore n \times \text{volume of barrel} = \text{volume of ink}$$
$$ \Rightarrow n \times \pi {r^2}h = \dfrac{1}{5} \times 1\,litre$$
$$ \Rightarrow n\pi {r^2}h = \dfrac{1}{5} \times 1000\,c{m^3}$$
$$ \Rightarrow n \times \dfrac{{22}}{7} \times \dfrac{1}{4} \times \dfrac{1}{4} \times 7 = 200\,c{m^3}$$
$$ \Rightarrow n = \dfrac{{200 \times 7 \times 4 \times 4}}{{22 \times 7}} = \dfrac{{1600}}{{11}}$$
Ink in one full barrel can write words = 3300
So, n barrels can write words = 3300 n
$$ = 3300 \times \dfrac{{1600}}{{11}} = 4,80,000$$
Hence, the required number of words = 4,80,000 words.
5. Water flows at the rate of 10m per min. through a cylindrical pipe 5mm in diameter. How long would it take to fill a conical vessel whose diameter at the base is 40cm and depth 24 cm?
Ans: When a fluid (water) flows through a pipe of a area of cross-section A with velocity v, then volume of water coming from pipe in time t
$$ = \text{Area of cross-section} \times \text{length}$$
$$ = \,A \times v.t\,[\because V = \text{Area of base} \times \text{Height}]$$
Cylinder | Cone |
$$A = \pi {r^2}$$ | $$R = \dfrac{{40}}{2}\,cm\, = 0.2\,m$$ |
$$r = \dfrac{{5\,mm}}{2} = \dfrac{5}{{2000}}m$$ | $$H = 24\,cm = 0.24\,m$$ |
The table will represents the given data of cylinder and cone
$$r = \dfrac{1}{{400}}m$$
$$v = 10\,m\,{\min ^{ - 1}}$$
$$ \Rightarrow v = \dfrac{{10}}{{60}}m{s^{ - 1}} = \dfrac{1}{6}m{s^{ - 1}}$$
Volume of flowing water = Volume of cone
$$ \Rightarrow Area\,\,of\,\,base \times height = \dfrac{1}{3}\pi {R^2}H$$
$$ \Rightarrow A \times v.t = \dfrac{1}{3}\pi {R^2}H$$
$$ \Rightarrow \pi {r^2}.v.t = \dfrac{1}{3}\pi {R^2}H$$
$$ \Rightarrow {r^2}.vt = \dfrac{1}{3}{R^2}H$$
$$ \Rightarrow \dfrac{1}{{400}} \times \dfrac{1}{{400}} \times \dfrac{1}{6}t = \dfrac{1}{3} \times 0.2 \times 0.2 \times 0.24$$
$$ \Rightarrow t = \dfrac{{2 \times 2 \times 24 \times 400 \times 400}}{{3 \times 10000}}$$
$$ \Rightarrow t = 4 \times 24 \times 4 \times 4 \times 2\sec $$
$$ = 51\min + 0.2\min = 51\min + 0.2 \times 60\sec $$
$$ \Rightarrow t = 51\min \,\,and\,\,12\sec $$
Hence, the conical tank will fill in 51 min and 12 sec.
6. A heap of rice is in the form of a cone of diameter 9m and height 3.5 m. Find the volume of rice. How much canvas cloth is required to just cover the heap?
Ans: The heap of rice is in the shape of cone, so
$$r = \dfrac{9}{2}m = 4.5m$$
$$h = 3.5m$$
$$V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3} \times \dfrac{{22}}{7} \times \dfrac{9}{2} \times \dfrac{9}{2} \times 3.5$$
$$ \Rightarrow V = \dfrac{{6237}}{{84}} = 74.25\,{m^3}$$
Hence, volume of rice = $$74.25\,{m^3}$$
For canvas:
Area of canvas = Curved surface area of cone $$ = \pi rl$$
$${l^2} = {r^2} + {h^2} = {(4.5)^2} + {(3.5)^2} = 20.25 + 12.25$$
$$ \Rightarrow {l^2} = 32.50$$
$$ \Rightarrow l = \sqrt {32.5} = 5.7m$$
Area of canvas $$ = \dfrac{{22}}{7} \times 4.5 \times 5.7 = 80.614$$
Area of canvas$$ = 80.614{m^2}$$
7. A factory manufactures 1,20,000 pencils daily. The pencils are cylindrical in shape each of length 25cm and circumference of base as 1.5cm. Determine the cost of coloring the curved surfaces of the pencils manufactured in one day at Rs. 0.05 per $${m^2}$$
Ans: Shape of the pencils is cylindrical. The height of pencil is h = 25 cm and the circumference is $$2\pi r = 1.5\,cm$$
Curved surface area of one pencil $$ = 2\pi rh$$
Therefore, curved surface area of 1,20,000 pencils
$$ = 1,20,000 \times 2\pi rh = 1,20,000 \times 1.5 \times 25c{m^2}$$
$$ = \dfrac{{1,20,000 \times 1.5 \times 25}}{{10 \times 100}}d{m^2} = 600 \times 75\,d{m^2}$$
Therefore the cost of coloring = $$600 \times 75 \times 0.05 = 2250$$
Hence, cost of coloring is Rs. 2250
8. Water is flowing at the rate of 15 km per hour through a pipe of diameter 14 cm into a cuboidal pond which is 50m long and 44m wide. In what time will the level of water in the pond rise by 21 cm?
Ans: Volume of flowing water = A.v.t. where, A = Area of cross-section of pipe or flowing water, v = Speed of water and t = time
Here, A is equivalent to area of base and height equal to distance (v.t) and we know that V = area of base $$ \times $$ height. The radius of the pipe is $$r = \dfrac{{14}}{2}cm = 7\,cm = 0.07\,m$$, the speed of the water is $$v = 15\dfrac{{km}}{{hr}} = 15000\dfrac{m}{{hr}}$$. The length, breadth and height of the pond is 50 m, 44 m and 21 cm = 0.21m
Volume of flowing water = Volume of same water in pond
$$A.v.t = l \times b \times h$$
$$ \Rightarrow \pi {r^2}.vt = l \times b \times h$$
$$ \Rightarrow \dfrac{{22}}{7} \times 0.07 \times 0.07 \times 15000 \times t(hrs.) = 50 \times 44 \times 0.21$$
$$ \Rightarrow t = \dfrac{{50 \times 44 \times 0.21 \times 7}}{{22 \times 0.07 \times 0.07 \times 15000}}$$
$$ \Rightarrow t = 20\,hrs$$
Hence, the time required is 20 hours.
9. A solid iron cuboidal block of dimensions $$4.4m \times 2.6m \times 1m$$ is recasted into a hollow cylindrical pipe of internal radius 30cm and thickness 5cm. Find the length of the pipe.
Ans: The length, breadth and height of the cuboid is 4.4m, 2.6 m and 1 m respectively. In the terms of centimetres given as 440cm, 260 cm and 100 cm.
The internal radius of the cylindrical pipe is $${r_1} = 30\,cm$$and the thickness is 5 cm. Therefore the external radius is $${r_2} = 30 + 5 = 35\,cm$$.
To find: The height of the cylindrical pipe.
Cuboid is recasted into a hollow cylindrical pipe.
$$ \Rightarrow lbh = \pi r_2^2H - \pi r_1^2H$$
$$ \Rightarrow lbh = \pi H[r_2^2 - r_1^2]$$
$$ \Rightarrow 440 \times 260 \times 100 = \dfrac{{22}}{7} \times H[{35^2} - {30^2}]$$
$$ \Rightarrow 1,14,40,000 = \dfrac{{22}}{7} \times H[1225 - 900]$$
$$ \Rightarrow H = \dfrac{{1,14,40,000 \times 7}}{{22 \times 325}}cm$$
$$ \Rightarrow H = 11200\,cm$$
$$ \Rightarrow H = 112m$$
Hence, the length of the pipe is 112 m.
10. 500 persons are taking a dip into a cuboidal pond which is 80m long and 50 m broad. What is the rise of water level in the pond, if the average displacement of the water by a person is 0.04$${m^3}$$ ?
Ans: Let the rise of water level in the pond be x m.
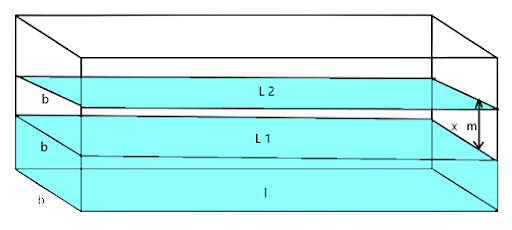
Let the water level before the persons took a dip was at $${L_1}$$. Now when 500 persons dipped into the pond, water level rises from $${L_1}$$ to $${L_2}$$ of height x m. The volume of water between two levels will be equal to the water displaced by 500 persons.
Volume of water raised = Volume of water replaced by 500 persons ( V of cuboid)
$$ \Rightarrow lbh = 500 \times 0.04$$
$$ \Rightarrow 80 \times 50 \times x = 500 \times 0.04$$
$$ \Rightarrow x = \dfrac{{500 \times 0.04}}{{80 \times 50}} = 0.005m = 0.5\,cm$$
Hence, the rise of water level in the pond is 0.5cm.
11. 16 glass spheres each of radius 2cm are packed into a cuboidal box of internal dimensions $$16\,cm \times 8\,cm \times 8\,cm$$ and then the box is filled with water. Find the volume of water. filled in the box.
Ans: The dimensions of a cuboidal box of 16 spheres is given as l = 16 cm, b = 8 cm and h = 8 cm and the radius of the sphere is given as r = 2 cm.
Volume of water filled in the box = Volume of box - Volume of 16 glass spheres
Vol. of water filled in the box $$ = lbh - 16.\dfrac{4}{3}\pi {r^3}$$
$$ = 16 \times 8 \times 8 - 16 \times \dfrac{4}{3} \times \dfrac{{22}}{7} \times 2 \times 2 \times 2$$
$$ = 1024 - \dfrac{{11264}}{{21}}$$
$$ = \dfrac{{21504 - 11264}}{{21}}$$
$$ = \dfrac{{10240}}{{21}}$$
$$ = 487.6\,c{m^3}$$
12. A milk container of height 16cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8cm and 20cm respectively. Find the cost of milk at the rate of Rs. 22 per L, which the container can hold.
Ans: The lower radius, upper radius and height of the milk container is given as 8 cm, 20 cm and 16 cm respectively.
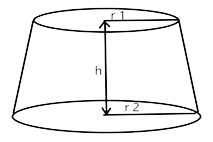
Volume of milk = Volume of frustum as it is filled completely
$$ = \dfrac{1}{3}\pi h(r_1^2 + r_2^2 + {r_1}{r_2})$$
$$ = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 16\,[{8^2} + {20^2} + 8 \times 20]$$
$$ = \dfrac{{352}}{{21}}\left[ {64 + 400 + 160} \right]$$
$$ = \dfrac{{219648}}{{21}}$$
$$ = 10459.428\,c{m^3} = 10.459\,litre$$
Volume of milk = 10.459 litre
Cost of milk $$ = Rs.\,22 \times 10.459 = \,Rs.\,230.098$$
Hence, the cost of milk $$ = \,Rs.\,230.098$$
13. A cylindrical bucket of height 32cm and base radius 18 cm is filled with sand. This bucket is emptied on the ground, and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Ans: By identifying the shapes, we have cones and cylinders. On reshaping from cylindrical to conical, the volume of sand emptied out remains the same.
The radius and height of the cylinder is given as R = 18 cm and H = 32 cm respectively. The height of the conical heap is given as h = 24 cm
To find: The radius and slant height of the conical heap


Volume of conical heap = Volume of cylinder
$$ \Rightarrow \dfrac{1}{3}\pi {r^2}h = \pi {R^2}H$$
$$ \Rightarrow \dfrac{1}{3}{r^2}h = {R^2}H$$
$$ \Rightarrow {r^2} = \dfrac{{3{R^2}H}}{h} = \dfrac{{3 \times 18 \times 18 \times 32}}{{24}} = 36\,cm$$
Radius of the conical heap is 36 cm.
On considering the Pythagoras theorem,$${l^2} = {r^2} + {h^2}$$
$$ = {(36)^2} + {(24)^2}$$
$$ = 1296 + 576$$
$$ = 1872$$
$$ \Rightarrow {l^2} = 1872$$
$$ \Rightarrow l = \sqrt {1872} = 43.266\,cm$$
Hence, radius and slant height are 36 cm and 43.2666 cm respectively.
14. A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of cylinder. The diameter and height of the cylinder are 6 cm and 12 cm, respectively. If the slant height of the conical portion is 5cm, then find the total surface area and volume of the rocket. (Use $$\pi $$= 3.14)
Ans: The radius and height of the cylinder is given as $$r = \dfrac{6}{2} = 3\,cm$$ and 12 cm respectively. The radius and the slant height of the cone is given by 3 cm and 5 cm respectively.
To find: The height of the cone
On considering the Pythagoras theorem we have $${l^2} = {r^2} + {h^2}\,\,or\,\,{h^2} = {l^2} - {r^2}$$
$$ \Rightarrow {h^2} = {5^2} - {3^2}$$
$$ \Rightarrow {h^2} = 25 - 9 = 16$$
$$ \Rightarrow h = 4\,cm$$
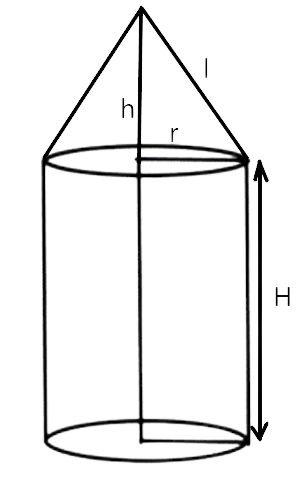
Now, volume of rocket = Volume of cylinder + Volume of cone
$$ = \pi {r^2}H + \dfrac{1}{3}\pi {r^2}h$$
$$ = \pi {r^2}\left[ {H + \dfrac{1}{3}h} \right]$$
$$ = 3.14 \times 3 \times 3\left[ {12 + \dfrac{1}{3} \times 4} \right]$$
$$ = 28.26\left[ {\dfrac{{36 + 4}}{3}} \right]$$
$$ = 28.26\left[ {\dfrac{{40}}{3}} \right]$$
$$ = 376.8\,c{m^3}$$
Volume of Rocket $$ = 376.8\,c{m^3}$$
Total surface area of rocket = Curved surface area of cylinder + Curved surface area of cone + Area of base of cylinder [As it is closed (Given)]
$$ = 2\pi rH + \pi rl + \pi {r^2}$$
$$ = \pi r\left[ {2H + l + r} \right]$$
$$ = 3.14 \times 3\left[ {2 \times 12 + 5 + 3} \right]$$
$$ = 3.14 \times 3 \times 32$$
$$ = 301.44\,c{m^2}$$
Hence, the surface area of rocket is $$301.44\,c{m^2}$$
15. A building is in the form of a cylinder surmounted by a hemispherical vaulted dome and contain $$41\dfrac{{19}}{{21}}\,{m^3}$$ of air. If the internal diameter of the dome is equal to its total height above the floor, find the height of the building.
Ans: The radius of Dome and cylinder is given by r. H = 2r
$$ \Rightarrow h + r = 2r$$
$$ \Rightarrow h = 2r - r = r$$
Volume of building $$ = 41\dfrac{{19}}{{21}} = \dfrac{{880}}{{21}}\,{m^3}$$
Vol. of cylinder + Vol. of hemisphere = $$\dfrac{{880}}{{21}}\,{m^3}$$
$$ \Rightarrow \pi {r^2}h + \dfrac{2}{3}\pi {r^3} = \dfrac{{880}}{{21}}\,$$
$$ \Rightarrow \pi {r^2}r + \dfrac{2}{3}\pi {r^3} = \dfrac{{880}}{{21}}\,\,$$
$$ \Rightarrow \pi {r^3} + \dfrac{2}{3}\pi {r^3} = \dfrac{{880}}{{21}}\,\,$$
$$ \Rightarrow \dfrac{5}{3}\pi {r^3} = \dfrac{{880}}{{21}}\,\,$$
$$ \Rightarrow {r^3} = \dfrac{{880 \times 3 \times 7}}{{21 \times 5 \times 22}}$$
$$ \Rightarrow {r^3} = 8$$
$$ \Rightarrow r = 2\,m$$
Hence, the height of the building is $$2 \times 2$$= 4 m.
16. A hemispherical bowl of internal radius 9 cm is full of liquid. The liquid is to be filled into cylindrical shaped bottles each of radius 1.5 cm and height 4 cm. How many bottles are needed to empty the bowl?
Ans: The radius and height of the cylindrical bottle is given as r = 1.5 cm and 4 cm respectively. The radius of the hemisphere is R = 9 cm
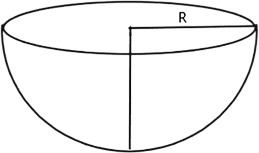
As the volume of liquid does not change
So, Volume of n bottles = Volume of hemisphere
$$ \Rightarrow n\pi {r^2}h = \dfrac{2}{3}\pi {R^3}$$
$$ \Rightarrow n{r^2}h = \dfrac{2}{3}{R^3}$$
$$ \Rightarrow n = \dfrac{{2{R^3}}}{{3{r^2}h}}$$
$$ \Rightarrow n = \dfrac{{2 \times {{(9)}^3}}}{{3 \times {{(1.5)}^2} \times 4}}$$
$$ \Rightarrow n = \dfrac{{2 \times 729}}{{3 \times 2.25 \times 4}}$$
$$ \Rightarrow n = 54$$
Hence, 54 bottles are needed.
17. A solid right circular cone of height 120cm and radius 60 cm is placed in a right circular cylinder full of water of height 180 cm such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is equal to the radius to the cone.
Ans: The radius and height of the cone is given as r = 60 cm and h = 120 cm respectively. The radius and height of cylinder is given as r = 60 cm and H = 180 cm
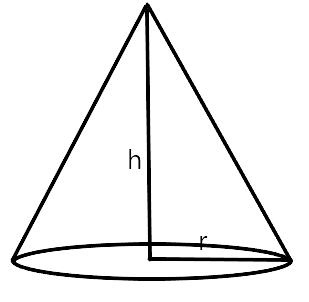
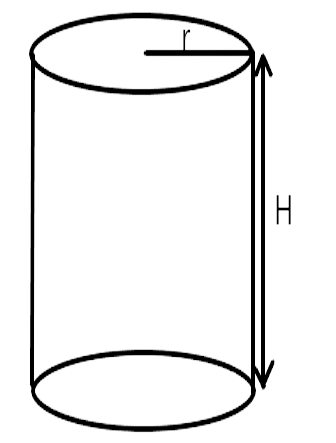
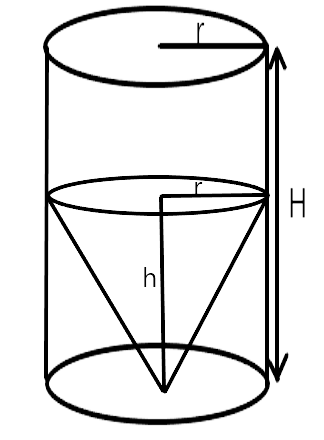
Cone is placed inside the cylindrical vessel full of water. So, the volume of water from the cylinder will overflow equal to the volume of the cone.
Hence, the water left in cylinder = Vol. of cylinder - Vol. of cone
Volume of water left after immersing the cone into cylinder full of water
= Volume of cylinder - Volume of cone
$$ = \pi {r^2}H - \dfrac{1}{3}\pi {r^2}h$$
Required volume of water in cylinder
$$ = \pi {r^2}\left[ {H - \dfrac{1}{3}h} \right]$$
$$ = \dfrac{{22}}{7} \times {(60)^2}\left[ {180 - \dfrac{{120}}{3}} \right]$$
$$ = \dfrac{{22}}{7} \times 3600 \times 140$$
$$ = 1584000\,c{m^3}$$
$$ = \dfrac{{1584000}}{{1000000}}\,{m^3}$$
$$ = 1.584\,{m^3}$$
Vol. of water in cylinder $$ = 1.584\,{m^3}$$
Hence, required volume of water left $$ = 1.584\,{m^3}$$
18. Water flows through a cylindrical pipe, whose inner radius is 1 cm at the rate of 80 cm per second in an empty cylindrical tank, the radius of whose base is 40 cm. What is the rise of the water level in a tank in half an hour?
Ans: Main concept: Volume of flowing water = A.v.t
Area of base = A = Area of cross-section of flowing water. As we know that distance is the product of speed and time. i.e., height = distance = speed $$ \times $$ time = v . t
Flowing water is filled in a cylindrical tank. Hence, the volume of flowing water is equal to the volume of water in a cylindrical tank. The speed of the flowing water is $$v = 80\,cm\,{s^{ - 1}}$$and the inner radius is 1 cm. The radius of the cylinder is R = 40 cm. The time taken for the water rise is $$t = \dfrac{1}{2}hr = \dfrac{1}{2} \times 3600\sec = 1800\sec $$
Volume of water in cylindrical tank = Volume of flowing water
$$ \Rightarrow \pi {R^2}H = A.v.t$$
$$ \Rightarrow \pi {R^2}H = \pi {r^2}v.t$$
$$ \Rightarrow {R^2}H = {r^2}v.t$$
$$ \Rightarrow 40 \times 40 \times H = 1 \times 1 \times 80 \times 1800$$
$$ \Rightarrow H = \dfrac{{80 \times 1800}}{{40 \times 40}}$$
$$ \Rightarrow H = 90\,cm$$
Hence, the rise of water level in the cylindrical tank is 90 cm.
19. The rainwater from a roof of dimensions 22m$$ \times $$20 m drains into a cylindrical vessel having diameter of the base 2m and height 3.5 m. If the rain water collected from the roof just fills the cylindrical vessel, then find the rainfall in cm.
Ans: The length, breadth and height of the cuboid is l = 22 m = 2200 cm, b = 20 m = 2000 cm and h = x cm respectively. The radius and height of the cylinder is given as r = 1 m = 100 cm and h = 3.5 m = 350 cm respectively.
If water from roof is not allowed to flow, then water level on roof rises upto x cm (let) then volume of cuboidal shape of water will be equal to the volume of cylinder.
Volume of rain water = Volume of cylinder
$$ \Rightarrow lbh = \pi {r^2}h$$
$$ \Rightarrow 2200 \times 2000 \times x = \dfrac{{22}}{7} \times 100 \times 100 \times 350$$
$$ \Rightarrow x = \dfrac{{22 \times 100 \times 100 \times 350}}{{7 \times 2200 \times 2000}} = 2.5\,cm$$
Hence, the rainfall is 2.5 cm.
20. A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins respectively. The dimensions of cuboid are 10 cm, 5cm, 4 cm. The radius of each conical depression is 0.5 cm and depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand.
Ans: A cuboidal piece of wood with depressions ( 4 cones and 1 cube) are made.
So, the volume of wood = Volume of cuboid - Volume of 4 cones - Volume of 1 cube
(Image will be upload soon)
Length of cuboid (l) = 10 cm
Breadth of cuboid (b) = 5 cm
Height of cuboid (h) = 4 cm
Radius of cone (r) = 0.5 cm
Height of cone (H) = 2.1 cm
Side of cube (a) = 3 cm
Hence, the volume of the wood in the entire pen stand
$$ = lbh - \left( {\dfrac{1}{3}\pi {r^2}H} \right) \times 4 - {a^3}$$
$$ = 10 \times 5 \times 4 - \dfrac{4}{3} \times \dfrac{{22}}{7} \times 0.5 \times 0.5 \times 2.1 - {(3)^3}$$
$$ = 200 - 2.2 - 27$$
$$ = 170.8\,c{m^3}$$
So, the volume of the wood in the pen stand after making depressions is $$170.8\,c{m^3}$$
About Class 10 Maths Chapter 12 - Surface Areas and Volumes
NCERT exemplar for Class 10 Maths, chapter 12 - surface areas and volumes is a good source for practice. Students learn during their theoretical Classes and work on their textbooks questions. As textbook questions are not enough for the practice purpose, the exemplar helps students practice by providing additional questions.
Students can get the exemplar for chapter - surface areas and volume on the Vedantu official website. These exemplar questions and their solutions are designed by the expert faculty of Vedantu. The exemplars are designed on the latest syllabus pattern advised by CBSE.
Students can find the exemplar in PDF form from Vedantu.com. Students can download the pdf for free by registering themselves on the website. Students can use the pdf for their preparation enhancement, also to clear their idea and doubt about formulas and practice the problems given in the pdf. These pdf include some difficult questions that students can undergo and practice the questions to be ready for the exams. As per last year’s question paper and sample papers, the questions given are of great help for the students. But these exemplars consists of other important topics that are mentioned below-
Surface areas for the combinations of solid objects.
The volume of the combination of solid objects.
Finding the volume and frustum of a cone, its surface area, and its total surface areas.
In chapter 12 - surface area and volumes, students will learn about the surface areas and volume of the solid shapes that are sphere, cylinder, cone-shaped solid, and cuboid as well as the other combinations of the solid shapes. Students will take some time while dealing with the chapter as they need to pay close attention to the topics that are a little tricky. For the help of the students to find the correct answers to the difficult questions and to solve the textbook problems, Vedantu avails the exemplar for the students.
Other Resources from Vedantu for Preparing Class 10 Chapter 12 NCERT Exemplar
Vedantu also offers online study material for Class 10 chapter 12 surface areas and volumes like exemplar books, notes, question papers, and NCERT solutions. The online study pattern with the latest pattern of the syllabus by CBSE board students can practice their learning. This new pattern of education will increase the efficiency and effectiveness of the students. Students will get personalized videos, that explain the hard topics like volume and surface area of solid shapes, etc. And this way of learning will enhance the learning of students.
Download the book exercise solutions for this chapter from Vedantu and prepare this chapter exceptionally. Master the concepts by following the solutions designed by the expert mentors of Vedantu and learn how to save time while solving these problems. Add this solution file to your study material and refer to it whenever you find a doubt at your convenience.
FAQs on NCERT Exemplar for Class 10 Maths Chapter 12 - Surface Areas and Volumes (Book Solutions)
1. Where can students find the NCERT Exemplar for Class 10 Maths Chapter 12 - Surface Areas and Volumes (Book Solutions)?
Students can find the exemplar solution in PDF form at Vedantu.com. Students can easily download the pdf for free by registering themselves on the website. They can use the pdf for their preparation enhancement, also to clear their idea and doubt about formulas and practice the problems given in the pdf. These pdf include some difficult questions that students can undergo and practice the questions to become ready for the exams. This will help them to be well versed in the subject.
2. Why should students practice NCERT Exemplar for Class 10 Maths Chapter 12 - Surface Areas and Volumes (Book Solutions)?
NCERT exemplar solution for Class 10 Maths Chapter 12 - surface areas and volumes is a good source for practice. Students learn during theoretical concepts in the classes and work on their textbooks questions. As textbook questions are not enough for the practice purpose, the exemplar will help students practice the additional questions. Students can get the exemplar for chapter - surface areas and volume on the Vedantu official website. These exemplar questions and their solutions are designed by the expert faculty of Vedantu for helping students to understand the concepts well and to focus on learning solving techniques. The exemplars are designed on the latest syllabus pattern advised by CBSE.
3. What topics and additional study material does the NCERT Exemplar for Class 10 Maths Chapter 12 - Surface Areas and Volumes (Book Solutions) consist of?
This pdf includes solutions to some difficult questions that students can practice before an exam. As per last year’s question paper and sample papers, the questions given are of great help for the students. But these exemplars consist of other important topics that are mentioned below- Surface areas for the combinations of solid objects, The volume of the combination of solid objects, Finding the volume and frustum of a cone, its surface area, and its total surface areas.
4. What are the learnings for the students from NCERT Exemplar for Class 10 Maths Chapter 12 - Surface Areas and Volumes (Book Solutions)?
In chapter 12 - surface area and volumes, students will learn about the surface areas and volume of the solid shapes that are sphere, cylinder, cone-shaped solid, and cuboid as well as the other combinations of the solid shapes. For the help of the students to find the correct answers to the difficult questions and to solve the textbook problems, Vedantu provides exemplar solutions for free. Students will find handling these tricky topics easier and convenient. Vedantu also offers online study material for Class 10 chapter 12 surface areas and volumes like exemplar books, notes, question papers, and NCERT solutions. The online study pattern with the latest pattern of the syllabus by CBSE board students can practice their learning.









































