Visualising Solid Shapes Class 7 Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 7 Maths Chapter 13 Visualising Solid Shapes Exercise 13.2 (2025-26)
1. Where can I find the correct step-by-step NCERT Solutions for Class 7 Maths Chapter 13, Visualising Solid Shapes?
You can find detailed, step-by-step NCERT Solutions for all exercises in Class 7 Maths Chapter 13 right here on Vedantu. These solutions are prepared by subject matter experts and strictly follow the CBSE 2025-26 syllabus and guidelines to ensure you learn the correct problem-solving methods.
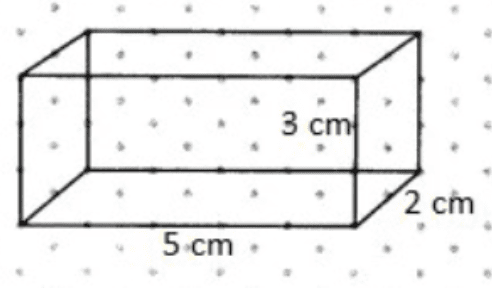
2. What is the correct method for drawing an isometric sketch of a cuboid as shown in the NCERT solutions?
The correct method for drawing an isometric sketch of a cuboid involves using an isometric dot sheet. The steps are:
- Start by drawing a rectangle for the front face.
- Draw lines backwards and upwards from the corners of the rectangle. These lines should be parallel and of equal length.
- Connect the ends of these lines to form the back face of the cuboid.
- Ensure all lines representing the length, breadth, and height follow the dot grid to maintain proportions.
3. How do the NCERT Solutions for Chapter 13 explain how to identify the different views of a solid shape?
The NCERT Solutions explain this by demonstrating a clear, methodical approach. To identify the top, front, and side views, you must imagine looking at the 3D object from that specific direction. For example, the front view is what you see when you look at the object head-on, the top view is what you see from directly above, and the side view is what you see from the side. The solutions provide solved examples with diagrams for various solids.
4. What key concepts are covered in the NCERT Solutions for Exercise 13.1 of Visualising Solid Shapes?
The NCERT Solutions for Exercise 13.1 primarily focus on identifying different nets that can be used to make cubes. The solutions provide a step-by-step verification method for each given net, showing how it can (or cannot) be folded to form a cube without any overlapping faces.
5. How can I use the NCERT solutions to verify Euler's formula for polyhedrons?
The NCERT Solutions guide you to verify Euler's formula (F + V - E = 2) systematically. For any given polyhedron, the correct method is:
- Step 1: Count the total number of faces (F).
- Step 2: Count the total number of vertices (V), which are the corners.
- Step 3: Count the total number of edges (E).
- Step 4: Substitute these values into the formula F + V - E. If the result is 2, the formula is verified for that shape.
6. Why is it important to draw solid shapes on an isometric dot sheet instead of plain paper when following the NCERT method?
Using an isometric dot sheet is crucial because it helps in drawing 3D objects with a more realistic sense of proportion and depth. Unlike plain paper, the dots are arranged in a triangular pattern, which allows you to easily draw lines at 60-degree angles to represent the three dimensions (length, width, height) accurately, making the sketch look three-dimensional as intended by the CBSE curriculum.
7. Beyond just getting the correct answer, what is the main purpose of solving problems on 'nets' in Chapter 13?
The main purpose of solving problems on nets is to develop your spatial reasoning and visualisation skills. By mentally folding a 2D net into a 3D shape, you learn to understand the relationship between two-dimensional representations and the three-dimensional objects they form. This skill is fundamental in fields like engineering, architecture, and design.
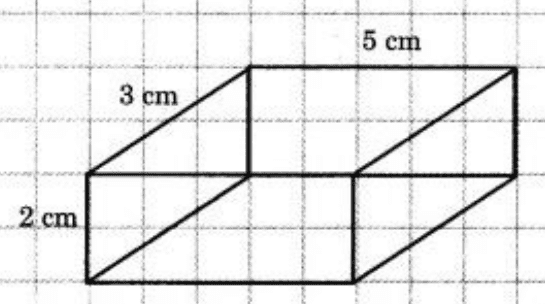
8. How do the problem-solving techniques for oblique sketches differ from those for isometric sketches in the NCERT solutions?
The key difference lies in how they represent 3D objects on a 2D plane.
- Oblique sketches are easier to draw; the front face is drawn true to its shape, and the depth is shown with parallel lines going back at an angle. However, they can look distorted.
- Isometric sketches provide a more realistic view where all dimensions are drawn to scale, but they require an isometric dot sheet for accuracy.
9. Can a single 3D shape, like a cube, have more than one correct net? How do the NCERT solutions handle this?
Yes, a single 3D shape can have multiple correct nets. For instance, a cube has 11 different possible nets. The NCERT solutions address this by presenting various configurations in the exercises and asking you to identify which ones will successfully fold into the shape. The solution for each problem provides a clear, step-by-step logical explanation for why a particular net works or fails.