NCERT Exemplar for Class 11 Physics Chapter 5 - Law of Motion (Book Solutions)

Exercise

MULTIPLE CHOICE QUESTIONS (TYPE-I)

5.1. A ball is travelling with uniform translatory motion. This means that:

(a) It is at rest.

(b) The path can be a straight line or circular and the ball travels with uniform speed.

(c) All particles of the ball have the same velocity (magnitude and direction) and the velocity is constant.

(d) The centre of mass the ball moves with constant velocity and the ball spins about its centre uniformly.

Ans: Option (c)

Uniform translatory motion occurs when all the particles of the body move with the same velocity in the same straight line. Hence, the correct answer is (c).

5.2. A meter scale is moving with uniform velocity. This implies

(a) The net acting on the scale is zero, but a torque about the centre of mass can act on the scale. 

(b) The net force acting on the scale is zero, and the net torque acting about the centre of mass of the scale is also zero.

(c) The net force acting on it need not be zero but the torque on it is zero.

(d) Neither the force nor the torque needs to be zero.

Ans: Option (b)

Since the body is moving with a uniform velocity, hence its acceleration is zero. This implies that the net force acting on it must be zero, which further makes the torque acting about the centre of mass of the scale also zero. Hence, the correct answer is (b).

5.3. A cricket ball of mass 150 g has the initial velocity $\overrightarrow u  = \left( {3\widehat i + 4\widehat j} \right)m{s^{ - 1}}$ and a final velocity $\overrightarrow v  =  - \left( {3\widehat i + 4\widehat j} \right)m{s^{ - 1}}$ after being hit. The change in momentum (final momentum – initial momentum) is (in kg ms-1-)

(a) zero

(b) $ - \left( {0.45\widehat i + 0.6\widehat j} \right)$

(c) $ - \left( {0.9\widehat i + 1.2\widehat j} \right)$

(d) $ - 5\left( {\widehat i + \widehat j} \right)$

Ans: Option (c)

Since momentum is given by $\overrightarrow p  = m\overrightarrow v $

Hence, $\Delta \overrightarrow p  = m\Delta \overrightarrow v  = m\left( {\overrightarrow v  - \overrightarrow u } \right) = m\left( { - \overrightarrow u  - \overrightarrow u } \right) =  - m\left( {2\overrightarrow u } \right)$

That is, $\Delta \overrightarrow p  =  - 0.15\left( {6\widehat i + 8\widehat j} \right) =  - \left( {0.9\widehat i + 1.2\widehat j} \right)$

Hence, the correct answer is (c).

5.4. In a previous problem 5.3, the magnitude of momentum transferred during the hit is:

(a) zero

(b) $0.75kgm{s^{ - 1}}$

(c) $1.5kgm{s^{ - 1}}$

(d) $1.4kgm{s^{ - 1}}$

Ans: Option (c)

Since we have $\Delta \overrightarrow p  =  - \left( {0.9\widehat i + 1.2\widehat j} \right)$

Therefore, the magnitude is $\left| {\Delta \overrightarrow p } \right| = \sqrt {{{\left( {0.9} \right)}^2} + {{\left( {1.2} \right)}^2}}  = \sqrt {0.81 + 1.44}  = \sqrt {225}  = 1.5kgm{s^{ - 1}}$

Hence, the correct answer is (c).

5.5. Conservation of momentum is a collision between particles can be understood from

(a) Conservation of energy

(b) Newton’s first law only

(c) Newton’s second law only

(d) Both Newton’s second and third law

Ans: Option (d) 

By the Newton’s second law of motion we can write $\dfrac{{dp}}{{dt}} = {F_{ext}}$

Since, by the law of conservation of momentum we have ${F_{ext}} = 0$

Therefore, $\dfrac{{dp}}{{dt}} = 0$

Hence momentum is constant.

Also by the Newton’s third law of motion, we have ${F_{12}} =  - {F_{21}}$

$\dfrac{{d{p_{12}}}}{{dt}} =  - \dfrac{{d{p_{21}}}}{{dt}} \Rightarrow d{p_{12}} =  - d{p_{21}}$

That gives $d{p_{12}} + d{p_{21}} = 0$

Here the law of conservation of momentum is proved.

Hence, the correct answer is (d).

5.6. A hockey player is moving northward and suddenly turns westward with the same speed to avoid an opponent. The force that acts on the player is:

(a) frictional force along westward

(b) muscle force along southward

(c) friction force along the south-west

(d) muscle force acting south-west

Ans: Option (c)

Since the frictional force always tries to resist the motion, hence the force that acts on the player moving northward and then suddenly turning westward is the frictional force acting along the south-west direction. Hence, the correct answer is (c).

5.7. A body of mass 2kg travels according to the law $x\left( t \right) = pt + q{t^2} + r{t^3}$ where $p = 3m/s,q = 4m{s^{ - 2}}{\text{ and }}r = 5m{s^{ - 3}}$ .The force acting on the body at t=2 seconds is:

(a) 136 N

(b) 134 N

(c) 158 N

(d) 68 N

Ans: Option (a)

Given that $x\left( t \right) = pt + q{t^2} + r{t^3}$ where $p = 3m/s,q = 4m{s^{ - 2}}{\text{ and }}r = 5m{s^{ - 3}}$

Hence, $x\left( t \right) = 3t + 4{t^2} + 5{t^3}$

Now, $F = ma = m\dfrac{{{d^2}x}}{{d{t^2}}}$

And $\dfrac{{{d^2}x}}{{d{t^2}}} = \dfrac{d}{{dt}}\left( {3 + 8t + 15{t^2}} \right) = 8 + 30t$

Now when $t = 2,m = 2$

Then $F = 2\left( {8 + 30 \cdot 2} \right) = 136N$

Hence, the correct answer is (a).

5.8. A body of mass 5 kg is acted upon by a force $\overrightarrow F  = \left( { - 3\widehat i + 4\widehat j} \right)N$ . If its initial velocity at t=0 is $\overrightarrow v  = \left( {6\widehat i - 12\widehat j} \right)m{s^{ - 1}}$ the time at which it will just have a velocity along the y axis is:

(a) never

(b) 10 s

(c) 2s

(d) 15s

Ans: Option (b)

Since $\overrightarrow a  = \dfrac{{\overrightarrow F }}{m}$ hence, we have $\overrightarrow a  = \dfrac{1}{5}\left( { - 3\widehat i + 4\widehat j} \right)N$

Now, since the x-component of the final velocity is zero,

Hence, ${v_x} = {u_x} + {a_x}t$

$0 = 6\widehat i + \dfrac{{ - 3\widehat i}}{5}t$

That gives us $t = 10s$

Hence, the correct answer is (b).

5.9. A car of mass m starts from rest and acquires a velocity $\overrightarrow v  = v\widehat i\left( {v > 0} \right)$ along east in two seconds. Assuming the car moves with uniform acceleration, the force exerted on the car is:

(a) $\dfrac{{mv}}{2}$ eastward and is exerted by the car engine.

(b) $\dfrac{{mv}}{2}$ eastward and is due to friction on tyres exerted by the road.

(c) more than $\dfrac{{mv}}{2}$ eastward exerted due to the engine and overcomes the friction of the road.

(d) $\dfrac{{mv}}{2}$ exerted by the engine.

Ans: Option (b)

Since we know that $\overrightarrow v  = \overrightarrow u  + \overrightarrow a t$ 

Here $\overrightarrow v  = v\widehat i,\overrightarrow u  = 0,t = 2$

Therefore, $v\widehat i = 0 + \overrightarrow a  \cdot 2$

Hence, $\overrightarrow a  = \dfrac{{v\widehat i}}{2}$

Now, $\overrightarrow F  = m\overrightarrow a  = \dfrac{{mv\widehat i}}{2}$

Therefore, the force $\dfrac{{mv\widehat i}}{2}$ acting on the car is due to the frictional force of $\dfrac{{mv\widehat i}}{2}$ which is acting towards the eastwards direction.

Hence, the correct answer is (b).

MULTIPLE CHOICE QUESTIONS-II

5.10. The motion of a particle of mass m is given by $x = 0$ for $t < 0s,x\left( t \right) = A\sin 4\pi t$ for $0 < t < \left( {\dfrac{1}{4}} \right)s$ (A>0) and $x = 0$ for $t > \left( {\dfrac{1}{4}} \right)s$ . Which of the following statements is true?

(a) The force at $t = \left( {\dfrac{1}{8}} \right)s$ on the particle is $ - 16{\pi ^2}Am$ .

(b) The particle is acted upon by on impulse of magnitude $4{\pi ^2}Am$ at $t = 0$ and $t = \left( {\dfrac{1}{4}} \right)s$

(c) The particle is not acted upon by any force.

(d) The particle is not acted upon by a constant force.

(e) There is no impulse acting on the particle

Ans: Options (a), (b) and (d)

Since the force acting on the particle is a function of time, hence it is not a constant force.

Now at $t = \left( {\dfrac{1}{8}} \right)s$ , we have $F = m\dfrac{{{d^2}x\left( t \right)}}{{d{t^2}}} = m \cdot A4\pi \dfrac{d}{{dt}}\left( {\cos 4\pi t} \right) = 4\pi Am\left( { - \sin 4\pi t} \right) \cdot 4\pi $

That is $F =  - 16{\pi ^2}Am\sin 4\pi t =  - 16{\pi ^2}Am\sin \left( {4\pi \dfrac{1}{8}} \right) =  - 16{\pi ^2}Am$

Now, since impulse is the change in momentum given by $\overrightarrow I  = \overrightarrow F  \cdot t$

Hence, $\overrightarrow I  =  - 16{\pi ^2}Am \cdot \dfrac{1}{4} =  - 4{\pi ^2}Am$

Hence, the correct answers are (a), (b) and (d).

5.11. In the given figure, the coefficient of friction between the floor and the body B is 0.1. The coefficient of friction between bodies B and A is 0.2. A force F is applied as shown on B. the mass of A is m/2 and of B is m. Which of the following statements are true?

(a) The bodies will move together if $\overrightarrow F  = 0.25mg$

(b) The body A will slip with respect to B if $\overrightarrow F  = 0.5mg$

(c) The bodies will move together if $\overrightarrow F  = 0.5mg$

(d) The bodies will be at rest if $\overrightarrow F  = 0.1mg$

(e) The maximum value of $\overrightarrow F $ for which the two bodies will move together is 0.45 mg.

Ans:  Options (a), (b) (d) and (e) 

Let the frictional force acting in the opposite directions on the bodies A and B be ${f_1}$ and ${f_2}$ respectively.

Now the common acceleration of bodies A and B will be given by

$ \Rightarrow a = \dfrac{{F - {f_1}}}{{m + \dfrac{m}{2}}} = \dfrac{{2\left( {F - {f_1}} \right)}}{{3m}}$

Hence the force on A is ${F_{AB}} = \dfrac{m}{2} \cdot \dfrac{{2\left( {F - {f_1}} \right)}}{{3m}} = \dfrac{{\left( {F - {f_1}} \right)}}{3}$

Now if ${F_{AB}}$ is equal or smaller than ${f_2}$ then the bodies will move together.

Hence, ${F_{AB}} = {f_2}$

So, $\dfrac{{\left( {F - {f_1}} \right)}}{3} = \dfrac{{\mu mg}}{2}$

Also, ${f_1} = \mu \left( {m + \dfrac{m}{2}} \right)g = 0.1 \cdot \dfrac{3}{2}g = 0.15g$

Hence we can write $\left( {F - {f_1}} \right) = \dfrac{{3\mu mg}}{2} = 1.5 \times 0.2 \times mg$

Or, $F = 0.30mg + {f_1} = 0.30mg + 0.15mg = 0.45mg$

Now the minimum force which can move A and B together is ${F_{\min }} \geqslant {f_1} + {f_2}$

That is ${F_{\min }} \geqslant 0.15mg + 0.2 \cdot \dfrac{m}{2}g$

Hence, ${F_{\min }} \geqslant 0.25mg$

Therefore only the option (c) is incorrect.

Hence, the correct answers are (a), (b), (d) and (e).

5.12. Mass ${m_1}$ moves on a slope making an angle θ with the horizontal and is attached to mass ${m_2}$ by a string passing over a frictionless pulley as shown in the figure. The coefficient of friction between ${m_1}$ and the sloping surface is μ. Which of the following statements are true?

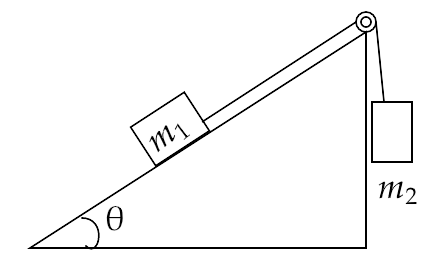
(a) If ${m_2} > {m_1}\sin \theta $ , the body will move up the plane.

(b) If ${m_2} > {m_1}\left( {\sin \theta  + \mu \cos \theta } \right)$ , the body will move up the plane.

(c) If ${m_2} < {m_1}\left( {\sin \theta  + \mu \cos \theta } \right)$ , the body will move up the plane.

(d) If ${m_2} < {m_1}\left( {\sin \theta  - \mu \cos \theta } \right)$ , the body will move up the plane.

Ans:  Options (b) and (d)

The system can be represented by the figure given below.

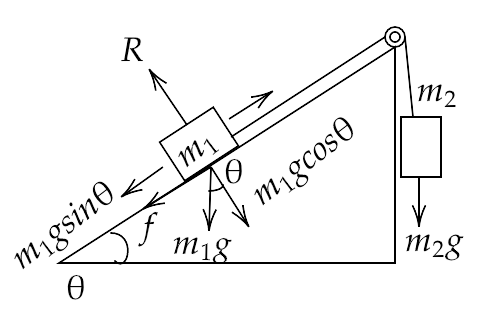
Here, we can write $f = \mu {m_1}g\cos \theta $

Now ${m_1}$ will go up and ${m_2}$ will go down when ${m_2}g - \left( {{m_1}g\cos \theta  + f} \right) > 0$

That gives ${m_2}g - {m_1}g\sin \theta  - \mu {m_1}g\cos \theta  > 0$

Or, ${m_2}g > {m_1}g\left( {\sin \theta  + \mu \cos \theta } \right)$

Hence, ${m_2} > {m_1}\left( {\sin \theta  + \mu \cos \theta } \right)$

Also, ${m_1}$ will go down and ${m_2}$ will go up when $ - f + {m_1}g\sin \theta  > {m_2}g$

That gives $ - \mu {m_1}g\cos \theta  + {m_1}g\sin \theta  > {m_2}g$

Or, ${m_1}\left( { - \mu \cos \theta  + \sin \theta } \right) > {m_2}$

Hence, ${m_2} < {m_1}\left( {\sin \theta  - \mu \cos \theta } \right)$

Therefore, the correct answers are (b) and (d).

5.13. In a given figure, a body A of mass m slides on a plane inclined at an angle ${\theta _1}$ to the horizontal and ${\mu _1}$ is the coefficient of friction between A and the plane. A is connected by a light string passing over a frictionless pulley to another body B, also of mass m, sliding on a frictionless plane inclined at angle ${\theta _2}$ to the horizontal. Which of the following statements are true?

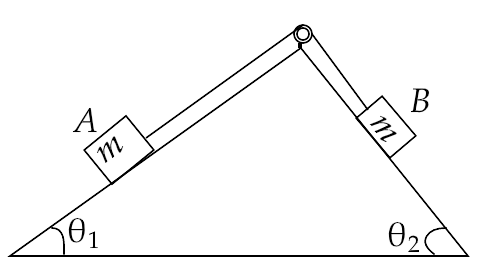
(a) A will never move up the plane.

(b) A will just start moving up the plane when $\mu  = \dfrac{{\sin {\theta _2} - \sin {\theta _1}}}{{\cos {\theta _1}}}$ .

(c) For A to move up the plane, ${\theta _2}$ must always be greater than ${\theta _1}$ .

(d) B will always slide down with constant speed.

Ans:  Options (b) and (c)

This system can be represented by the figure given below.

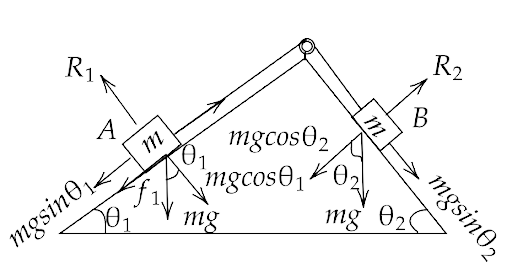
Here we have $f = \mu mg\cos {\theta _1}$

Now, the body A will move up and body B will move down the plane,

If $mg\sin {\theta _1} + f = mg\sin {\theta _2}$

That gives us, $mg\sin {\theta _1} + \mu mg\cos {\theta _1} = mg\sin {\theta _2}$

Or, $\mu \cos {\theta _1} = \sin {\theta _2} - \sin {\theta _1}$

Hence, $\mu  = \operatorname{s} \dfrac{{in{\theta _2} - \sin {\theta _1}}}{{\cos {\theta _1}}}$

Also, the body A will move down and body B will move up the plane,

If $mg\sin {\theta _2} - mg\sin {\theta _1} > 0$

Or, $\sin {\theta _2} > \sin {\theta _1}$

Hence, ${\theta _2} > {\theta _1}$

Hence, the correct answers are (b) and (c).

5.14. Two billiard balls A and B, each of mass 50g and moving in opposite directions with speed of 5m/s each, collide and rebound with the same speed. If the collision lasts for ${10^{ - 3}}s$ which of the following statements are true?

(a) The impulse imparted to each ball is 0.25 kg m/s and the force on each ball is 250 N.

(b) The impulse imparted to each ball is 0.25 kg m/s and the force exerted on each ball is $25 \times {10^{ - 5}}N$ .

(c) The impulse imparted to each ball is 0.5 Ns.

(d) The impulse and the force on each ball are equal in magnitude and opposite in direction.

Ans:  Options (c) and (d)

We are given that, $m = 0.05kg$ and $v = 5m/s$

Hence we have initial momentum of each ball $p = mv = 0.05 \times 5 = 0.25kgm{s^{ - 1}}$

After collision, both balls will move in opposite directions

Hence, we have final momentum of each ball $p' =  - mv =  - 0.05 \times 5 =  - 0.25kgm{s^{ - 1}}$

Now the impulse is the change in momentum,

Hence, $I = p' - p =  - 0.25 - 0.25 =  - 0.5kgm{s^{ - 1}}$

Therefore, the correct answers are (c) and (d).

5.15. A body of mass 10kg is acted upon by two perpendicular forces, 6 N and 8 N. The resultant acceleration of the body is

(a) $1m{s^{ - 2}}$ at an angle of ${\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right)$ w.r.t. 6 N force.

(b) $0.2m{s^{ - 2}}$ at an angle of ${\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right)$ w.r.t. 6 N force.

(c) $1m{s^{ - 2}}$ at an angle of ${\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right)$ w.r.t. 8 N force.

(d) $0.2m{s^{ - 2}}$ at an angle of ${\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right)$ w.r.t. 8 N force.

Ans:  Options (a) and (c)

Since the two forces are acting perpendicular, hence their resultant force will be given by,

$ \Rightarrow R = \sqrt {{8^2} + {6^2}}  = \sqrt {64 + 36}  = \sqrt {100}  = 10N$

Hence the acceleration will be 

$ \Rightarrow a = \dfrac{F}{m} = \dfrac{R}{{10}} = \dfrac{{10}}{{10}} = 1m{s^{ - 2}}$

Now we have $\tan {\theta _1} = \dfrac{8}{6} = \dfrac{4}{3} \Rightarrow {\theta _1} = {\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right)$

And $\tan {\theta _2} = \dfrac{6}{8} = \dfrac{3}{4} \Rightarrow {\theta _2} = {\tan ^{ - 1}}\left( {\dfrac{3}{4}} \right)$

Therefore, the correct answers are (a) and (c).

VERY SHORT ANSWER TYPE QUESTIONS

5.16. A girl riding a bicycle along a straight road at a speed of $5m{s^{ - 1}}$ throws a stone of mass 0.5 kg which has a speed of $15m{s^{ - 1}}$ with respect to the ground along with her direction of motion. The mass of the girl and bicycle is 50 kg. Does the speed of the bicycle change after the stone is thrown? What is the change in speed, if so?

Ans: Given that, $m = 50kg$ and $m' = 0.5kg$

Also their initial velocities are $u = 5m{s^{ - 1}}$ and $u' = 5m{s^{ - 1}}$

And their final velocities are $v$ and $v' = 15m{s^{ - 1}}$

Now according to the law of conservation of momentum, we have the total initial momentum equal to the total final momentum.

Therefore, $\left( {m + m'} \right)u = mv + m'v'$

That gives, $\left( {50 + 0.5} \right)5 = 50v + \left( {0.5} \right) \cdot 15$

Hence, $v = \dfrac{{245}}{{50}} = 4.9m{s^{ - 1}}$

Therefore the change in speed is $5 - 4.9 = 0.1m{s^1}$ .

5.17. A person of mass 50 kg stands on a weighing scale on a lift. If the lift is descending with a downward acceleration of $9m{s^{ - 2}}$ what would be the reading of the weighing scale? $\left( {g = 10m{s^{ - 2}}} \right)$

Ans: Since the lift is moving downwards, hence it will result in a decrease in the weight of the person.

The new weight of the person inside the lift will be given by $W' = m\left( {g - a} \right)$

Hence, $W' = 50\left( {10 - 9} \right) = 50N$

Now the reading of the weighing scale will be $\dfrac{{W'}}{g} = \dfrac{{50}}{{10}} = 5kg$

5.18. The position-time graph of a body of mass 2 kg is as given in Figure. What is the impulse on the body at t= 0s and t= 4s?

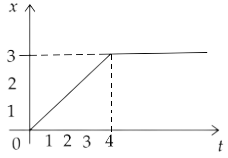
Ans: From the figure, we can see that the graph is a straight line between t= 0s and t= 4s , hence the velocity is constant in this period.

The final velocity will be given by the slope of the graph,

Hence $v = \tan \theta  = \dfrac{3}{4} = 0.75m/s$

Since the velocity is zero at t= 0s and t= 4s  ,hence the momentum is also zero at these two points.

Now since impulse is change in momentum,

Hence, the impulse at t= 0s is $2\left( {0.75} \right) - 0 = 1.5Ns$

Similarly, the impulse at t= 4s is $0 - 2\left( {0.75} \right) =  - 1.5Ns$

Therefore, the impulse first increased at t= 0s by $1.5Ns$ and then decreased at t= 4s by $1.5Ns$ .

5.19. A person driving a car suddenly applies the brakes on seeing a child on the road ahead. If he is not wearing the seat belt, he falls forward and hits his head against the steering wheel. Why?

Ans: When the car is moving with some velocity, then the person is also moving with the same velocity. After applying the brakes, the car stops suddenly. The lower part of the driver stops along with the car but the upper part of the person continues to move with the existing velocity. This results in the person hitting his head against the steering wheel due to the inertia of motion.

5.20. The velocity of a body of mass 2 kg as a function of t is given by $\overrightarrow v \left( t \right) = 2t\widehat i + {t^2}\widehat j$ . Find the momentum and the force acting on it, at time t= 2 s.

Ans: Given that $m = 2kg$ and $\overrightarrow v \left( t \right) = 2t\widehat i + {t^2}\widehat j$

Momentum at t= 2 s will be given by $p = mv = 2 \cdot \left( {2t\widehat i + {t^2}\widehat j} \right)$

That gives us, $p = \left( {4t\widehat i + 2{t^2}\widehat j} \right)kgm{s^{ - 1}}$

Since $t = 2$ , hence $p = \left( {8\widehat i + 8\widehat j} \right)$

Also the force acting on it will be given by 

$ \Rightarrow \overrightarrow F  = m\overrightarrow a  = m\dfrac{{d\overrightarrow v }}{{dt}} = m\dfrac{d}{{dt}}\left( {2t\widehat i + {t^2}\widehat j} \right) = m\left( {2\widehat i + 2t\widehat j} \right)$

Since $t = 2$  and $m = 2kg$ , hence

$ \Rightarrow \overrightarrow F  = 2\left( {2\widehat i + 4\widehat j} \right) = 4\widehat i + 8\widehat jN$

5.21. A block placed on a rough horizontal surface is pulled by a horizontal force F. Let f be the force applied by the rough surface on the block. Plot a graph of f versus F.

Ans: For the smaller values of the applied force the frictional force increases linearly upto the limiting friction as shown in the graph below.

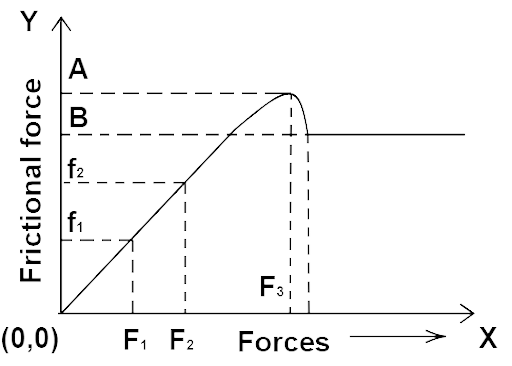
After crossing the maximum point of the static friction the frictional force becomes constant and does not change due to the kinetic friction.

5.22. Why are porcelain objects wrapped in paper or straw before packing for transportation?

Ans: Due to the brittle nature of porcelain objects, they can be broken even after getting a small jerk while transportation. Wrapping objects in paper and straw helps in increasing the time taken to stop or change their velocity instead of a sudden motion or break. Also, decreasing the acceleration $a = \dfrac{{\left( {v - u} \right)}}{t}$ of the objects results in smaller forces acting on it.

5.23. Why does a child feel more pain when she/he falls down on a hard cement floor than when she/he falls on the soft muddy ground in the garden?

Ans: Since the mass and velocities in both the cases are same, the only way to decrease the amount of force experienced while hitting the ground is to increase the time taken during the contact because we have $F = ma = m\dfrac{{\left( {v - u} \right)}}{t}$ .

A cement floor is hard in nature and takes very little amount of time while hitting it whereas a muddy ground is soft in nature and takes more time during the impact and hence decreases the experienced force.

5.24. A woman throws an object of mass 500 g with speed of $25m{s^{ - 1}}$ .

(a) What is the impulse imparted to the objects?

Ans: Given that the mass of the object is $m = 500g = 0.5kg$ and its initial and final velocities are $u = 0$ and $v = 25m{s^{ - 1}}$ respectively.

Now the impulse imparted to the object will be given by,

$ \Rightarrow \overrightarrow F  \cdot dt = \dfrac{{d\overrightarrow p }}{{dt}} \cdot dt = d\overrightarrow p  = m\overrightarrow v  - m\overrightarrow u $

That gives,

$ \Rightarrow I = \overrightarrow F  \cdot dt = m\left( {\overrightarrow v  - \overrightarrow u } \right) = 0.5\left( {25 - 0} \right) = 1.25Ns$

(b) If the object hits a wall and rebounds with half the original speed, what is the change in momentum of the object?

Ans: Now if the object  bounces back with half the original velocity,

Then we have $m = 500g = 0.5kg$ and $u = 25m{s^{ - 1}}$ and $v =  - \dfrac{{25}}{2}m{s^{ - 1}}$

Then the change in momentum will be given by,

$ \Rightarrow \Delta \overrightarrow p  = m\left( {\overrightarrow v  - \overrightarrow u } \right) = 0.5\left( { - \dfrac{{25}}{2} - 25} \right) = 0.5 \times \left( { - \dfrac{{75}}{2}} \right)$

Hence,

$ \Rightarrow \Delta \overrightarrow p  =  - 18.75kgm{s^{ - 1}}$

5.25. Why are mountain roads generally made winding upwards rather than going straight up?

Ans: While going upwards on an inclined plane or a mountain which has a slope, the force of friction acting on a vehicle of mass m is given by $f = \mu mg\cos \theta $ where $\theta $ is the angle of inclination with the horizontal surface. When the road is winded upwards, i.e. when $\theta $ is small, then the force of friction is high and there are less possibilities of skidding or rolling backwards. Whereas, if $\theta $ is high as in a straight up road, then the frictional force will be small and there are high chances of skidding and causing accidents.

SHORT ANSWER TYPE QUESTIONS

5.26. A mass of 2kg is suspended with thread AB (figure). Thread CD of the same type is attached to the other end of 2 kg mass. Lower thread is pulled gradually, harder and harder in the downward direction so as to apply force on AB. Which of the threads will break and why?

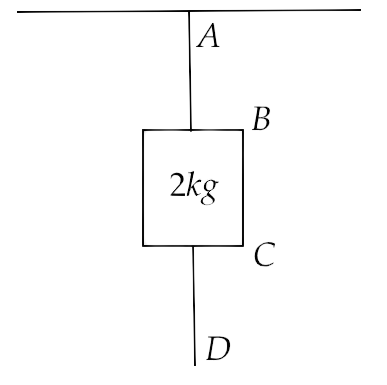
Ans: When the thread CD is pulled downwards then the force acting at point C is equal to the force applied at point D  acting downwards. Whereas the force acting at point A is equal to the sum of force applied on CD and the force acting downwards due to the suspended mass of 2kg. Since, the force acting at point A is 2kg more than point C, therefore thread AB will break from the point A.

5.27. In the above-given problem if the lower thread is pulled with a jerk, what happens?

Ans: If thread CD is pulled with a jerk then it will break from the point C because the force acting at point C is not moving further to the point A due to the inertia of the rest of the suspended mass of 2kg.

5.28. Two masses of 5 kg and 3 kg are suspended with help of massless inextensible strings as shown in Figure. Calculate ${T_1}{\text{ and }}{T_2}$ when whole system is going upwards with acceleration $ = 2m{s^{ - 2}}$ (use $g = 9.8m{s^{ - 2}}$ )

Ans: Given that, the whole system is going in the upward direction with an acceleration $a = 2m{s^{ - 2}}$

Also, we have $g = 9.8m{s^{ - 2}}$ , ${m_1} = 5kg,{m_2} = 3kg$

Now we know that the tension in a string is always equal and opposite in all parts of the string.

Hence, forces acting on mass ${m_1}$ are

$ \Rightarrow {T_1} - {T_2} - {m_1}g = {m_1}a$

That is,

$ \Rightarrow {T_1} - {T_2} - 5g = 5a$

Or,

$ \Rightarrow {T_1} - {T_2} = 5a + 5g = 5\left( {a + g} \right) = 5\left( {2 + 9.8} \right)$

Hence,

$ \Rightarrow {T_1} - {T_2} = 5\left( {11.8} \right) = 59.0N$

Similarly, forces acting on mass ${m_2}$ are

$ \Rightarrow {T_2} - {m_2}g = {m_2}a$

That is,

$ \Rightarrow {T_2} - 3g = 3a$

Or,

$ \Rightarrow {T_2} = 3a + 3g = 3\left( {a + g} \right) = 3\left( {2 + 9.8} \right)$

Hence,

$ \Rightarrow {T_2} = 3\left( {11.8} \right) = 35.4N$

Now that gives us ${T_1} = 59.0N + {T_2} = 59.0 + 35.4 = 94.4N$

5.29. Block A of weight 100 N rests on a frictionless inclined plane of slope angle 30° (Figure). A flexible cord attached to A passes over a frictionless pulley and is connected to block B of weight W. Find the weight W for which the system is in equilibrium.

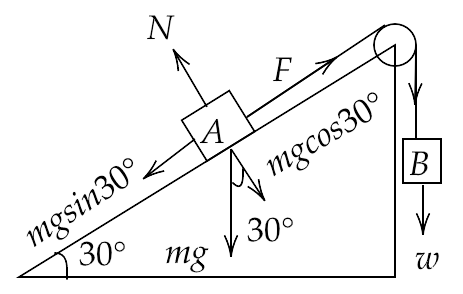
Ans: For the given system to be in an equilibrium, there must be no motion i.e. the frictional force must be equal to zero.

Now, for the balanced condition of A and B, we have

$ \Rightarrow mg\sin \theta  = F$

That gives us,

$ \Rightarrow mg\sin 30^\circ  = F$

Or,

$ \Rightarrow F = \dfrac{1}{2}mg$

Since $mg = 100N$ is given

Therefore,

$ \Rightarrow F = \dfrac{1}{2} \cdot 100$

i.e.

$ \Rightarrow F = 50N$

Hence the weight of the block is $50N$ .

5.30. A block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, calculate the minimum force required to be applied by the finger to hold the block against the wall?

Ans: Let F be the force applied by the finger on the block of mass M in order to hold it against the wall.

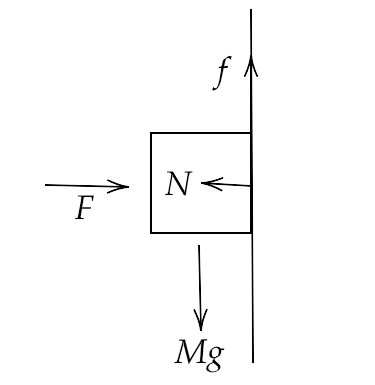
For the equilibrium condition, we have $F = N$ and $f = Mg$

That gives us,

$ \Rightarrow f = \mu F = Mg$

Hence,

$ \Rightarrow F = \dfrac{{Mg}}{\mu }$

Therefore, the minimum force required to hold the block against the wall at rest is $F = \dfrac{{Mg}}{\mu }$ .

5.31. A 100kg gun fires a ball of 1kg horizontally from a cliff of height 500m. It falls on the ground at a distance of 400 m from the bottom of the cliff. Find the recoil velocity of the gun. (acceleration due to gravity = $10m{s^{ - 2}}$ )

Ans: Let the final velocity of the ball be ${v_b}$.

Since it is fired horizontally, its vertical component is zero.

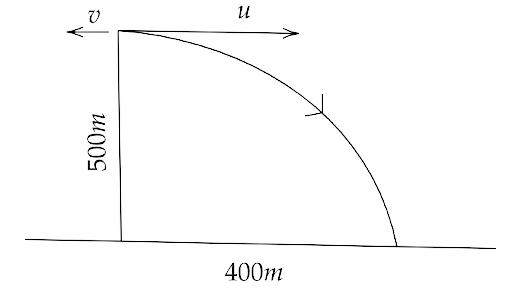
Now for the vertically downward motion of the ball, we have

$ \Rightarrow s = ut + \dfrac{1}{2}a{t^2}$

That gives us,

$ \Rightarrow 500 = 0 + \dfrac{1}{2}\left( {10} \right){t^2}$

Or,

$ \Rightarrow \dfrac{{500}}{5} = {t^2}$

Hence,

$ \Rightarrow t = \sqrt {100}  = 10s$

Now, we can write ${v_b} = \dfrac{{400}}{{10}} = 40m{s^{ - 1}}$

Now using the law of conservation of momentum we can write,

$ \Rightarrow {m_b}{u_b} + {{\rm M}_g}{u_g} = {m_b}{v_b} + {M_g}{v_g}$

That gives us,

$ \Rightarrow 0 + 0 = 1 \cdot 40 + 100{v_g}$

Hence,

$ \Rightarrow {v_g} =  - \dfrac{{40}}{{100}}$

i.e.

$ \Rightarrow {v_g} =  - 0.4m{s^{ - 1}}$

Therefore , the recoil velocity of the gun is $ - 0.4m{s^{ - 1}}$ i.e. in the opposite direction of the ball.

5.32. Figure (a) and (b), shows (x, t), (y, t) diagrams of a particle moving in 2 dimensions If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.

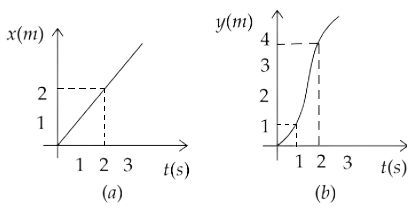
Ans: From the graph (a), we have $x = t$

Hence,

$ \Rightarrow {v_x} = \dfrac{{dx}}{{dt}} = \dfrac{{d\left( t \right)}}{{dt}} = 1m{s^{ - 1}}$

Since the velocity is constant, hence we have

$ \Rightarrow {a_x} = \dfrac{{{d^2}x}}{{d{t^2}}} = \dfrac{{d{v_x}}}{{dt}} = 0$

Therefore, ${F_x} = m{a_x} = 0.5 \times 0 = 0N$ towards X-axis

Now, from the graph (b), we have $y = {t^2}$

Hence,

$ \Rightarrow {v_y} = \dfrac{{dy}}{{dt}} = \dfrac{{d\left( {{t^2}} \right)}}{{dt}} = 2t$

Now the acceleration will be given by,

$ \Rightarrow {a_y} = \dfrac{{{d^2}y}}{{d{t^2}}} = \dfrac{{d{v_y}}}{{dt}} = \dfrac{{d2t}}{{dt}} = 2m{s^{ - 1}}$

Therefore, ${F_y} = m{a_y} = 0.5 \times 2 = 1N$ towards Y-axis

Now their resultant force will be given by,

$ \Rightarrow F = \sqrt {{F_x}^2 + {F_y}^2}  = \sqrt {0 + 1}  = 1N$ towards Y-axis

33. A person in an elevator accelerating upwards with an acceleration of $2m{s^{ - 2}}$ , tosses a coin vertically upwards with a speed of$20m{s^{ - 1}}$ . After how much time will the coin fall back into his hand? ( $g = 10m{s^{ - 2}}$ )

Ans: When an elevator is moving upwards with an acceleration $2m{s^{ - 2}}$ , then the effective acceleration of the elevator is given by $a' = a + g = 2 + 10 = 12m{s^{ - 2}}$

Now for the effectives motion of the coin we have $u = 20m{s^{ - 1}}$ and $v = 0$  and $a' =  - 12m{s^{ - 2}}$ since the acceleration is opposite to the motion of the coin.

Let the time of coin to achieve the maximum height be t

Then we have,

$ \Rightarrow v = u + at$

That gives us,

$ \Rightarrow 0 = 20 - 12t$

Hence,

$ \Rightarrow t = \dfrac{{20}}{{12}} = \dfrac{5}{3}s$

So the time to reach the maximum height is $t = \dfrac{5}{3}s$

Hence, time taken by the coin to fall back into the hand will be given by,

$ \Rightarrow 2t = 2 \times \dfrac{5}{3}s = \dfrac{{10}}{3} = 3.33s$

LONG ANSWER TYPE QUESTIONS

5.34. There are three forces ${\overrightarrow F _1},{\overrightarrow F _2}{\text{ and }}{\overrightarrow F _3}$ acting on a body, all acting on a point P on the body. The body is found to move with uniform speed.

(a) Show that the forces are coplanar.

Ans: It is given that due to the three forces ${\overrightarrow F _1},{\overrightarrow F _2}{\text{ and }}{\overrightarrow F _3}$ , the body moves with a uniform speed.

Therefore, the acceleration due to these forces is zero.

That gives us the resultant force also equal to zero.

Hence,

$ \Rightarrow {\overrightarrow F _1} + {\overrightarrow F _2} + {\overrightarrow F _3} = 0$

$ \Rightarrow {\overrightarrow F _3} =  - \left( {{{\overrightarrow F }_1} + {{\overrightarrow F }_2}} \right)$

This relation states that the force ${\text{ }}{\overrightarrow F _3}$ is the resultant force of the other two forces ${\overrightarrow F _{1{\text{ }}}}{\text{and }}{\overrightarrow F _2}$ but has a negative sign, that means it has the opposite direction.

Therefore if the two forces ${\overrightarrow F _{1{\text{ }}}}{\text{and }}{\overrightarrow F _2}$ are on the same plane, then the force ${\text{ }}{\overrightarrow F _3}$ will also be on the same plane but having the opposite direction.

Hence the three forces ${\overrightarrow F _1},{\overrightarrow F _2}{\text{ and }}{\overrightarrow F _3}$ are coplanar.

(b) Show that the torque acting on the body about any point due to these three forces is zero.

Ans: Now, since the resultant of these forces is zero, so the torque acting on the body at any point will also be zero as,

$ \Rightarrow \overrightarrow \tau   = \overrightarrow F  \times r = \left( {{{\overrightarrow F }_1} + {{\overrightarrow F }_2} + {{\overrightarrow F }_3}} \right) \times r = 0 \times r = 0$

5.35. When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time $pT$ , where p is some number greater than one. Calculate the coefficient of friction between the body and the rough plane.

Ans: Given that, the body slides down from an inclined plane making an angle of 45° with the horizontal, taking time T.

The effective acceleration of the body in this case will be $a = g\sin 45^\circ  = \dfrac{g}{{\sqrt 2 }}$

Now for this motion we can write,

$ \Rightarrow s = ut + \dfrac{1}{2}a{t^2}$

That gives us,

$ \Rightarrow s = 0 \cdot T + \dfrac{1}{2}\dfrac{g}{{\sqrt 2 }}{T^2}$

Or,

$ \Rightarrow s = \dfrac{{g{T^2}}}{{2\sqrt 2 }}$

Now considering the motion of the body along rough inclined plane, we have

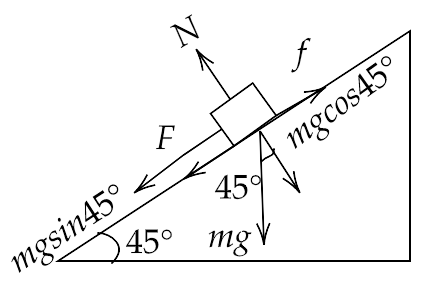
In this case,  for the equilibrium condition we can write

$ \Rightarrow ma = mg\sin 45^\circ  - f$

That gives,

$ \Rightarrow ma = \dfrac{{mg}}{{\sqrt 2 }} - \mu mg\cos 45^\circ $

Or,

$ \Rightarrow ma = \dfrac{{mg}}{{\sqrt 2 }} - \mu \dfrac{{mg}}{{\sqrt 2 }} = \dfrac{{mg}}{{\sqrt 2 }}\left( {1 - \mu } \right)$

Hence,

$ \Rightarrow a = \dfrac{g}{{\sqrt 2 }}\left( {1 - \mu } \right)$

Now if $t = pT,s = s,a = \dfrac{g}{{\sqrt 2 }}\left( {1 - \mu } \right)$

Then we have

$ \Rightarrow s = ut + \dfrac{1}{2}a{t^2}$

That gives,

$ \Rightarrow s = 0 \cdot pT + \dfrac{1}{2}\dfrac{g}{{\sqrt 2 }}\left( {1 - \mu } \right){p^2}{T^2}$

Or,

$ \Rightarrow s = \dfrac{g}{{2\sqrt 2 }}\left( {1 - \mu } \right){p^2}{T^2}$

Now since the distance in both the cases are equal,

Therefore, we have

$ \Rightarrow \dfrac{g}{{2\sqrt 2 }}\left( {1 - \mu } \right){p^2}{T^2} = \dfrac{{g{T^2}}}{{2\sqrt 2 }}$

That gives us,

$ \Rightarrow \left( {1 - \mu } \right){p^2} = 1$

Or,

$ \Rightarrow \left( {1 - \mu } \right) = \dfrac{1}{{{p^2}}}$

Hence,

$ \Rightarrow \mu  = \left( {1 - \dfrac{1}{{{p^2}}}} \right)$

5.36. Figure (a) and (b) shows $\left( {{v_x} - t} \right)$ and $\left( {{v_y} - t} \right)$ diagrams for a body of unit mass. Find the force, as a function of time.

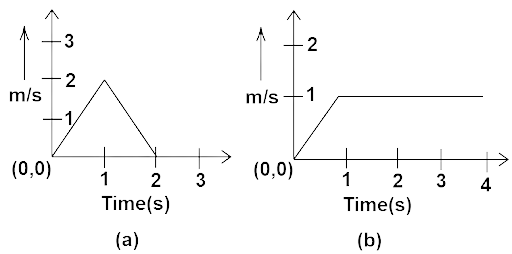
Ans: In the figure (a), we have ${v_x} = 2t$ for t<1s and ${v_x} = 2\left( {2 - t} \right)$ for 1s<t<2s

Hence the acceleration between 0s to 1s will be given by,

$ \Rightarrow {a_x} = \dfrac{{d{v_x}}}{{dt}} = \dfrac{{d2t}}{{dt}} = 2m{s^{ - 2}}$

Also ${F_x} = m{a_x} = 1 \times 2 = 2N$ for t<1s

And the acceleration between 1s to 2s will be given by,

$ \Rightarrow {a_x} = \dfrac{{d{v_x}}}{{dt}} = \dfrac{{2d\left( {2 - t} \right)}}{{dt}} =  - 2m{s^{ - 2}}$

Also ${F_x} = m{a_x} = 1 \times \left( { - 2} \right) =  - 2N$ for 1s<t<2s

Now in figure (b), we have ${v_y} = t$ for t<1s and ${v_y} = 1$ for t>1s

Hence the acceleration between 0s to 1s will be given by,

$ \Rightarrow {a_y} = \dfrac{{d{v_y}}}{{dt}} = \dfrac{{dt}}{{dt}} = 1m{s^{ - 2}}$

Also ${F_y} = m{a_y} = 1 \times 1 = 1N$ for t<1s

And the acceleration between 1s to 3s will be given by,

$ \Rightarrow {a_y} = \dfrac{{d{v_y}}}{{dt}} = \dfrac{{d1}}{{dt}} = 0m{s^{ - 2}}$

Also ${F_y} = m{a_y} = 1 \times 0 = 0N$ for t>1s

Now the resultant force will be given by,

$ \Rightarrow \overrightarrow F  = \overrightarrow {{F_x}} \widehat i + \overrightarrow {{F_y}} \widehat j$

Hence,

$ \Rightarrow \overrightarrow F  = 2\widehat i + \widehat j$ for t<1s

And,

$ \Rightarrow \overrightarrow F  =  - 2\widehat i$ for 1s<t<2s

And,

$ \Rightarrow \overrightarrow F  = 0$ for t>2s

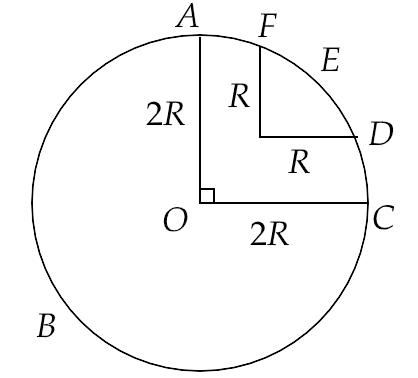
5.37. A racing car travels on a track (without banking) ABCDEFA (Figure). ABC is a circular arc of radius 2R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The coefficient of friction on the road is μ = 0.1. The maximum speed of the car is $50m{s^{ - 1}}$ . Find the minimum time for completing one round.

Ans: Since a given circular path is unbanked, hence the necessary centripetal force is provided by the frictional force.

Hence, we have $\dfrac{{m{v^2}}}{r} = \mu mg$

Or,

$ \Rightarrow v = \sqrt {\mu gr} $

Now consider each part of the circular path separately.

For the path ABC, we have

$ \Rightarrow d = \dfrac{3}{4}2\pi \left( {2R} \right) = 3\pi  \cdot 100 = 300\pi m$

Hence,

$ \Rightarrow v = \sqrt {\mu gr}  = \sqrt {0.1 \times 10 \times 2R}  = \sqrt {200}  = 10\sqrt 2  = 14.14m/s$

That gives,

$ \Rightarrow {t_{ABC}} = \dfrac{{300\pi }}{{14.14}} = 66.62s$

For the path CD and FA, we have

$ \Rightarrow d = R + R = 2R = 200m$

Since CD and FA are straight path, hence $ \Rightarrow v = 50m/s$

That gives,

$ \Rightarrow {t_{CD + FA}} = \dfrac{{200}}{{50}} = 4s$

For the path DEF, we have

$ \Rightarrow d = \dfrac{1}{4}2\pi \left( R \right) = \dfrac{{\pi  \cdot 100}}{2} = 50\pi m$

Hence,

$ \Rightarrow v = \sqrt {\mu gr}  = \sqrt {0.1 \times 10 \times R}  = \sqrt {00}  = 10m/s$

That gives,

$ \Rightarrow {t_{DEF}} = \dfrac{{50\pi }}{{10}} = 15.7s$

Therefore, total time taken by the car to cover the complete distance is,

$ \Rightarrow t = {t_{ABC}} + {t_{CD + FA}} + {t_{DEF}}$

Hence,

$ \Rightarrow t = 66.62 + 4 + 15.7$

i.e.

$ \Rightarrow t = 86.32s$

5.38. The displacement vector of a particle of mass m is given by

$\overrightarrow r \left( t \right) = \widehat iA\cos \omega t + \widehat jB\sin \omega t$

(a) Show that the trajectory is an ellipse.

Ans: Given that $\overrightarrow r \left( t \right) = \widehat iA\cos \omega t + \widehat jB\sin \omega t$

Let $x = A\cos \omega t$ and $y = B\sin \omega t$

That gives us,

$ \Rightarrow \dfrac{x}{A} = \cos \omega t$  ...(1)

And,

$ \Rightarrow \dfrac{y}{B} = \sin \omega t$  ...(2)

Now squaring and adding these two equations gives us,

$ \Rightarrow \dfrac{{{x^2}}}{{{A^2}}} + \dfrac{{{y^2}}}{{{B^2}}} = {\cos ^2}\omega t + {\sin ^2}\omega t$

Hence,

$ \Rightarrow \dfrac{{{x^2}}}{{{A^2}}} + \dfrac{{{y^2}}}{{{B^2}}} = 1$

Therefore the trajectory of the particle is an ellipse.

(b) Show that $\overrightarrow F  =  - m{\omega ^2}\overrightarrow r $

Ans: Since $x = A\cos \omega t$

Hence,

$ \Rightarrow {v_x} = \dfrac{{dx}}{{dt}} = \dfrac{{dA\cos \omega t}}{{dt}} =  - A\omega \sin \omega t$

And

$ \Rightarrow {a_x} = \dfrac{{d{v_x}}}{{dt}} = \dfrac{{d\left( { - A\omega \sin \omega t} \right)}}{{dt}} =  - {\rm A}{\omega ^2}\cos \omega t$

Also, $y = B\sin \omega t$

Hence,

$ \Rightarrow {v_y} = \dfrac{{dy}}{{dt}} = \dfrac{{dB\sin \omega t}}{{dt}} = B\omega \cos \omega t$

And,

$ \Rightarrow {a_y} = \dfrac{{d{v_y}}}{{dt}} = \dfrac{{dB\omega \cos \omega t}}{{dt}} =  - B{\omega ^2}\sin \omega t$

Therefore, the resultant acceleration will be

$ \Rightarrow a = {a_x} + {a_y}$

That gives us,

$ \Rightarrow \overrightarrow a  =  - {\rm A}{\omega ^2}\cos \omega t\widehat i - B{\omega ^2}\sin \omega t\widehat j$

Or,

$ \Rightarrow \overrightarrow a  =  - {\omega ^2}\left( {{\rm A}\cos \omega t\widehat i + B\sin \omega t\widehat j} \right)$

Hence,

$ \Rightarrow \overrightarrow a  =  - {\omega ^2}\overrightarrow r $

Now since, $\overrightarrow F  = m\overrightarrow a $

Therefore,

$ \Rightarrow \overrightarrow F  =  - m{\omega ^2}\overrightarrow r $

Hence proved.

5.39. A cricket bowler releases the ball in two different ways:

(a) giving it only horizontal velocity, and

Ans: In case (a),

For horizontal motion, we have ${u_x} = {v_s} = {v_x}$

And for vertical motion, we have ${v_y}^2 = {u_y}^2 + 2gH$

Since in this case we are given that ${u_y} = 0$

Hence, ${v_y} = \sqrt {2gH} $

So the resultant velocity is $v = \sqrt {{v_x}^2 + {v_y}^2}  = \sqrt {{v_s}^2 + 2gH} $

(b) giving it horizontal velocity and a small downward velocity. The speed ${v_s}$ at the time of release is the same. Both are released at a height H from the ground. Which one will have greater speed when the ball hits the ground? Neglect air resistance.

Ans: For horizontal motion, we have ${u_x} = {v_s} = {v_x}$

And for vertical motion, we have ${v_y}^2 = {u_y}^2 + 2gH$

Hence, ${v_y} = \sqrt {{u_y}^2 + 2gH} $

So the resultant velocity is $v' = \sqrt {{v_x}^2 + {v_y}^2}  = \sqrt {{v_s}^2 + {u_y}^2 + 2gH} $

Comparing these two resultant velocities, we get $v' > v$

Therefore, in case (b) will have a greater speed when the ball hits the ground.

5.40. There are four forces acting at a point P produced by strings as shown in the figure, which is at rest. Find the forces ${F_1}{\text{ and }}{F_2}$ .

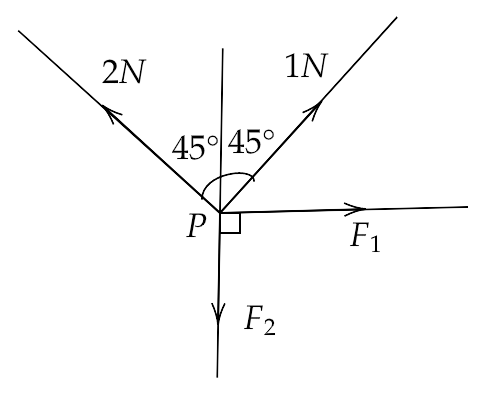
Ans: Since the particle is at rest which means it has no acceleration and the resultant force due to all the forces must be zero. Therefore, the components of the forces along X and Y axes will also be zero. Now, for the equilibrium condition along the X-axis, we have

$ \Rightarrow {F_x} = 0$

That gives us,

$ \Rightarrow {F_1} + 1\cos 45^\circ  - 2\cos 45^\circ  = 0$

Hence,

$ \Rightarrow {F_1} - \cos 45^\circ  = 0$

Or,

$ \Rightarrow {F_1} = \cos 45^\circ $

That is,

$ \Rightarrow {F_1} = \dfrac{1}{{\sqrt 2 }}N$

Also, for the equilibrium condition along the Y-axis, we have

$ \Rightarrow {F_y} = 0$

That gives us,

$ \Rightarrow  - {F_2} + 1\cos 45^\circ  + 2\cos 45^\circ  = 0$

Or,

$ \Rightarrow  - {F_2} =  - 3\cos 45^\circ $

Hence,

$ \Rightarrow {F_2} = \dfrac{3}{{\sqrt 2 }}N$

5.41. A rectangular box lies on a rough inclined surface. The coefficient of friction between the surface and the box is μ. Let the mass of the box be m.

(a) At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane?

Ans: The above given system can be represented by the figure drawn below:

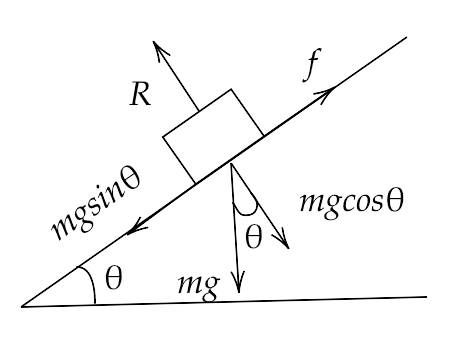
(a) The box will start to slide down the plane if $f = \mu N = mg\sin \theta $

i.e. when

$ \Rightarrow \mu mg\cos \theta  = mg\sin \theta $

That gives,

$ \Rightarrow \mu  = \tan \theta $

Hence,

$ \Rightarrow \theta  = {\tan ^{ - 1}}\mu $

(b) What is the force acting on the box down the plane, if the angle of inclination of the plane is increased to α > θ?

Ans: Now if $\alpha  > \theta $ then the box will slide down i.e. the net force will be acting downwards.

Hence, we have

$ \Rightarrow {F_1} = mg\sin \alpha  - f$

Or,

$ \Rightarrow {F_1} = mg\sin \alpha  - \mu mg\cos \alpha $

That gives us,

$ \Rightarrow {F_1} = mg\left( {\sin \alpha  - \mu \cos \alpha } \right)$

(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed?

Ans: To keep the box stationary or move upwards with a uniform speed, the net force 

must be acting upwards.

Hence, we have

$ \Rightarrow {F_2} = mg\sin \alpha  + f$

Or,

$ \Rightarrow {F_2} = mg\sin \alpha  + \mu mg\cos \alpha $

That gives us,

$ \Rightarrow {F_2} = mg\left( {\sin \alpha  + \mu \cos \alpha } \right)$

(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a?

Ans: The box will move upwards with an acceleration a if we have,

$ \Rightarrow {F_3} - mg\sin \alpha  - f = ma$

Or,

$ \Rightarrow {F_3} - mg\sin \alpha  - \mu mg\cos \alpha  = ma$

That gives us,

$ \Rightarrow {F_3} = mg\sin \alpha  + \mu mg\cos \alpha  + ma$

Hence,

$ \Rightarrow {F_3} = mg\left( {\sin \alpha  + \mu \cos \alpha } \right) + ma$

5.42. A helicopter of mass 2000kg rises with a vertical acceleration of $15m{s^{ - 2}}$ . The total mass of the crew and passengers is 500 kg. Give the magnitude and direction of the ( $g = 10m{s^{ - 2}}$ ).

(a) Force on the floor of the helicopter by the crew and passengers.

Ans: Given that $a = 15m{s^{ - 2}}$ , $g = 10m{s^{ - 2}}$ , $m = 500kg$  and $M = 2000kg$

The force on the floor of the helicopter by the crew and passengers will be given by

$ \Rightarrow F = m\left( {g + a} \right)$

That gives us,

$ \Rightarrow F = 500\left( {10 + 15} \right)$

Hence,

$ \Rightarrow F = 12500{\rm N}$ acting downwards

(b) The action of the rotor of the helicopter on the surrounding air.

Ans: The action of the rotor of the helicopter on the surrounding air will be equal to the reaction force by Newton’s third law.

Hence, we have

$ \Rightarrow F = \left( {m + M} \right)\left( {g + a} \right)$

That gives us,

$ \Rightarrow F = \left( {500 + 2000} \right)\left( {10 + 15} \right)$

Or,

$ \Rightarrow F = \left( {2500} \right)\left( {25} \right)$

Hence,

$ \Rightarrow F = 62500N$ acting downwards

(c) Force on the helicopter due to the surrounding air.

Ans: Force on the helicopter due to the surrounding air is the reaction force which is equal and opposite to the action force by the third law of Newton.

Therefore,

$ \Rightarrow F =  - \left( {{\text{Action Force}}} \right)$

i.e.

$ \Rightarrow F =  - \left( {m + M} \right)\left( {g + a} \right)$

That gives us,

$ \Rightarrow F =  - \left( {500 + 2000} \right)\left( {10 + 15} \right)$

That is,

$ \Rightarrow F =  - \left( {2500} \right)\left( {25} \right)$

Hence,

$ \Rightarrow F =  - 62500N$ acting downwards

Or,

$ \Rightarrow F = 62500N$ acting upwards

Chapter Details

After learning the quantitative description of the motion of a particle in the chapters of 'Motion in a Straight Line' and 'Motion in a Plane,' it's time to learn about the various rules and natural laws governing it.  'Law of Motion' defines the various principles followed by the objects in moving in a three-dimensional space. As the movement of objects depends on various external agencies of the environment, this chapter examines and establishes the laws of inertia and force acting on a body of mass in motion.

You will come to know about any previous philosophers or scientists such as Aristotle belonging to the common era before Christ, in section 5.2 ‘Aristotle's Fallacy,’  Galileo Galilei of the sixteenth and seventeenth century, or Sir Isaac Newton of the seventeenth and eighteenth century. They all are considered the originators of modern-day physics. Newton explained the condition and effect of various forces acting over a body of the motion. The three laws of motion mentioned in sections 5.4, 5.5, and 5.6 given by Newton are universal in nature and it is very important to learn and by heart them. These laws are later used to explain the momentum of the objects in motion and its conservation as well as in equilibrium in sections 5.7 ‘Conservation of Momentum’ and 5.8 ‘Equilibrium of a Particle’. Later the chapter delves us into the more intricate studies about ‘Common Forces of Mechanics’ in section 5.9 such as ‘Friction.’ It includes the sub-topics such as ‘Static Friction,’ and ‘Rolling Friction.’

Section 5.10 about ‘Circular Motion’ has been explained taking an example of a car running around a turning on a levelled road and a banked road. 12 example solutions in this chapter have made it easy to understand.  Finally, the chapter has tried to solve the problems in mechanics to make us clear about how to apply the laws while solving the problems in section 5.11 “Solving Problems in Mechanics.’

As said, always solving the problems provided in the exercises is very important for understanding the laws of motion and it's appropriate application. You can use the solved papers of the exercises provided by vedantu.com free of cost. You can download the paper from this page directly and also use it as a reference before solving the problems.