Chemistry Notes for Chapter 8 Organic Chemistry Some Basic Principles And Techniques Class 11 - FREE PDF Download
FAQs on Organic Chemistry Some Basic Principles And Techniques Class 11 Chemistry Chapter 8 CBSE Notes - 2025-26
1. What are the core concepts to summarise from Class 11 Chemistry Chapter 8, Organic Chemistry: Some Basic Principles and Techniques for the 2025-26 session?
For a quick revision of this chapter, you should focus on summarising these key areas: the tetravalency of carbon, IUPAC nomenclature rules, the different types of isomerism (structural and stereoisomerism), fundamental concepts in reaction mechanisms like electron displacement effects (inductive, resonance), and the basics of qualitative and quantitative analysis of organic compounds.
2. Is Chapter 8, 'Some Basic Principles and Techniques,' the same as General Organic Chemistry (GOC) in Class 11?
Yes, this chapter is commonly referred to as General Organic Chemistry (GOC). It lays the essential foundation for all subsequent organic chemistry topics by covering the principles of structure, naming, isomerism, and the electronic effects that govern chemical reactions.
3. How should one quickly revise the priority of functional groups for IUPAC nomenclature?
For efficient revision, remember the general priority order for the principal functional group. A simplified summary is:
- Carboxylic acids
- Sulphonic acids
- Esters
- Acid chlorides
- Amides
- Nitriles
- Aldehydes
- Ketones
- Alcohols
- Amines
- Ethers & Alkenes/Alkynes
Remembering the top 5-6 in order is crucial for solving most nomenclature problems.
4. What is the most efficient way to summarise the different types of electron displacement effects for revision?
To quickly revise electron displacement effects, focus on their key differences:
- Inductive Effect: A permanent effect involving the shifting of sigma (σ) electrons due to electronegativity differences. It weakens with distance.
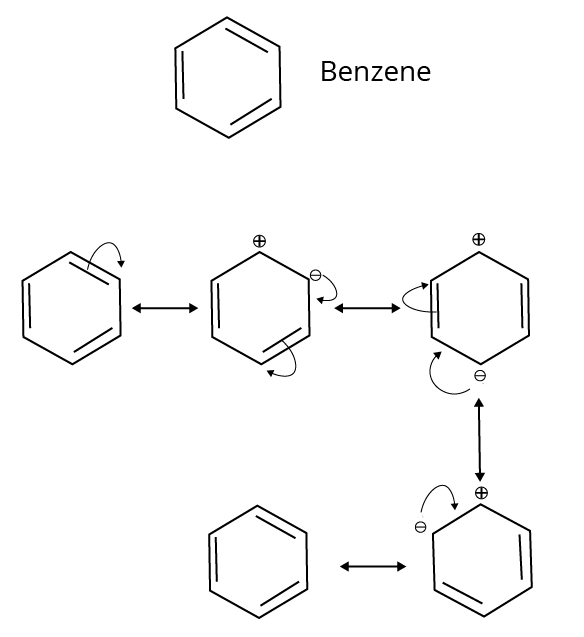
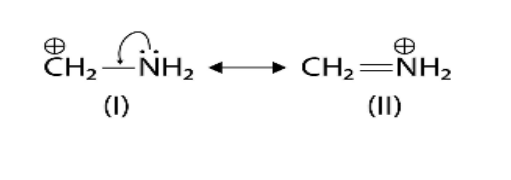
- Resonance (Mesomeric) Effect: A permanent effect involving the delocalisation of pi (π) electrons or lone pairs in a conjugated system.
- Electromeric Effect: A temporary effect involving the complete transfer of a shared pair of pi (π) electrons to one of the atoms in the presence of an attacking reagent.
- Hyperconjugation: Involves the delocalisation of sigma (σ) electrons of a C-H bond of an alkyl group directly attached to an unsaturated system or an atom with an unshared p-orbital.
5. What key points should be remembered about the different methods for purifying organic compounds?
For revision, associate each purification method with its core principle:
- Crystallisation: Based on the difference in solubilities of the compound and its impurities in a suitable solvent.
- Distillation: Used to separate volatile liquids from non-volatile impurities or liquids with a sufficient difference in boiling points.
- Chromatography: Based on the differential adsorption of components of a mixture on an adsorbent.
- Sublimation: Used for solids that can pass directly to the vapour state from the solid state.
6. How does the concept of hybridisation (sp³, sp², sp) help in quickly summarising the geometry of simple organic molecules?
Hybridisation provides a quick summary of a molecule's shape. sp³ hybridisation (e.g., in methane) involves only sigma bonds, resulting in a tetrahedral geometry with bond angles of 109.5°. sp² hybridisation (e.g., in ethene) involves one pi bond, leading to a trigonal planar geometry with 120° angles. sp hybridisation (e.g., in ethyne) involves two pi bonds, resulting in a linear geometry with 180° angles.
7. Why is understanding resonance crucial for predicting the stability of organic intermediates?
Understanding resonance is vital because it is a key factor in stability. When a reactive intermediate like a carbocation or free radical can exhibit resonance, the charge or the odd electron is not localised on a single atom. Instead, it is delocalised (spread out) over multiple atoms. This dispersal of charge significantly increases the stability of the intermediate. Generally, the more resonance structures an intermediate has, the more stable it is.
8. What is the fundamental difference between homolytic and heterolytic bond cleavage, and how does it determine the reaction pathway?
The fundamental difference lies in how the shared electron pair in a covalent bond is split. In homolytic cleavage, the bond breaks symmetrically, with each atom taking one electron, forming highly reactive free radicals. This pathway is common in non-polar conditions (e.g., presence of UV light). In heterolytic cleavage, the bond breaks asymmetrically, with one atom taking both electrons, forming ions (a cation and an anion). This pathway is favoured in polar solvents.
9. How do the inductive and resonance effects differ in their operation and impact on a molecule's reactivity?
While both affect reactivity, they operate differently. The inductive effect is transmitted through the chain of sigma (σ) bonds and its influence decreases significantly with distance from the source group. The resonance effect, however, is transmitted through the pi (π) bond system (conjugated systems) and its influence can extend across the entire system without diminishing, making it a much stronger effect in most cases.