Mensuration Class 8 Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 8 Maths Chapter 9 Mensuration Exercise 9.1 - 2025-26
1. What concepts are covered in NCERT Solutions for Class 8 Maths Chapter 9 Mensuration Exercise 9.1 as per CBSE 2025–26?
Class 8 Maths Chapter 9 Mensuration Exercise 9.1 covers calculation of areas of two-dimensional shapes. Topics include:
- Area of trapezium
- Area of quadrilaterals and special quadrilaterals
- Area of polygons, including division into triangles and rectangles for calculation
- Application of formulas for regular polygons and sum of interior angles
2. How do NCERT Solutions for Class 8 Maths Chapter 9 ensure students follow the correct CBSE solving methodology?
Vedantu’s NCERT Solutions for Class 8 Maths Chapter 9 use a stepwise approach:
- Each answer demonstrates proper use of CBSE-recommended formulas.
- Solutions are broken into clear steps: identifying shape, substituting values, systematic calculation, and writing the final answer with units.
- Strategies are explained for choosing the appropriate formula based on shape and given data.
- Explanations reinforce why each mathematical step is necessary, preventing shortcut mistakes.
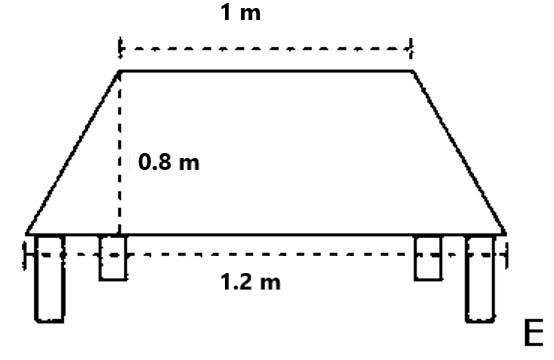
3. What is the formula to find the area of a trapezium in Class 8 Maths Chapter 9, and when should it be used?
The area of a trapezium is given by:
Area = ½ × (sum of parallel sides) × height
Use this formula whenever you're given:
- Two sides that are parallel
- The perpendicular distance (height) between those sides
4. What are common misconceptions students face while calculating area in Mensuration Exercise 9.1?
Common mistakes include:
- Mixing up the lengths of parallel and non-parallel sides in a trapezium
- Failing to use perpendicular distance as height
- Not converting all measurements to the same units before calculation
- Adding instead of averaging for polygon interior angle sums
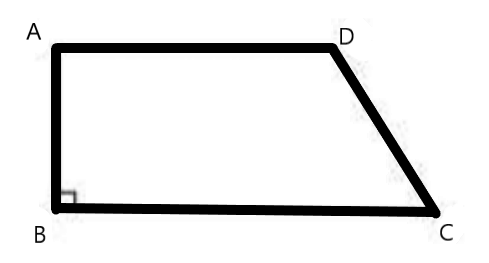
5. In Chapter 9 Mensuration Ex 9.1, how can the area of irregular quadrilaterals be calculated using NCERT methods?
According to CBSE 2025–26 guidelines:
- Split the quadrilateral into two triangles by drawing a diagonal
- Calculate the area of each triangle using ½ × base × height
- Add the two areas together for total area
6. Why is unit consistency crucial in solving NCERT Mensuration problems for Class 8 Maths?
Consistent units ensure correctness of the final answer. For example:
- If one side is in cm and another in m, convert both to the same unit before computation
- Errors in unit conversion can lead to incorrect area or perimeter values
7. What stepwise approach should be followed to solve polygon area questions in NCERT Solutions Class 8 Maths Chapter 9?
For polygons:
- Identify the type of polygon (triangle, quadrilateral, regular polygon, etc.)
- Break complex polygons into simpler known shapes
- Apply the relevant area formula to each shape
- Sum all calculated areas for total result
8. How are application-based Mensuration problems addressed in NCERT Solutions for Class 8 Maths Chapter 9 Exercise 9.1?
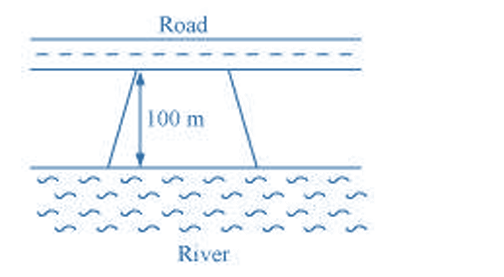
Application-based questions often describe real-life scenarios, such as fields, tiles, or frames. The approach involves:
- Translating the word problem into a geometric diagram
- Identifying dimensions and required shapes
- Selecting correct formulas and performing calculations with units
- Explicitly mentioning cost, area, or lengths as required by the question
9. What is the importance of practicing NCERT Solutions for Class 8 Maths Chapter 9 Exercise 9.1 for CBSE exams?
Practicing these solutions helps students to:
- Build confidence in geometry calculations
- Understand proper use of area and perimeter formulas
- Learn how to structure answers and show correct working steps
- Identify and fix conceptual gaps before the exam
10. FUQ: If a question provides only the area and one diagonal of a rhombus, how can a student use NCERT Solutions logic to find the other diagonal?
When given area (A) and one diagonal (d₁):
- Use the formula: A = ½ × d₁ × d₂
- Rearrange to solve for the unknown diagonal: d₂ = 2A / d₁
11. FUQ: How do Class 8 Mensuration solutions handle cases when the diagram or required dimensions are missing in the question?
If a required dimension (like height or side) is missing:
- Use details given such as perimeter, sum of sides, or total area to form equations
- Apply algebraic strategies, such as expressing unknowns in terms of knowns, and solving stepwise
- Check for logical deductions, e.g., perimeter minus known sides gives the length of the missing side
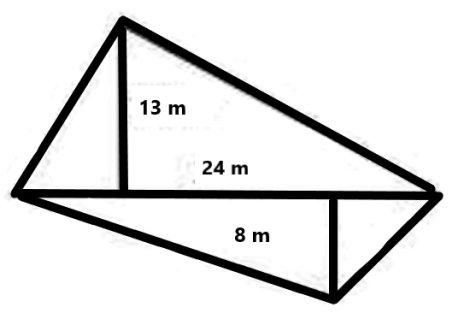
12. FUQ: What if the given shape is a composite figure, not directly specified in the syllabus?
CBSE encourages breaking composite figures into standard shapes:
- Divide the figure into rectangles, trapeziums, and triangles
- Calculate the area of each smaller section individually
- Sum the areas for the total composite area
13. FUQ: How does Vedantu’s NCERT Solutions help students avoid formula misapplication in Class 8 Mensuration?
Vedantu’s Class 8 Mensuration solutions:
- Clearly explain each formula’s context and limitations
- Warn against common traps, such as using parallelogram area formula for irregular quadrilaterals
- Include steps for verifying shape type before applying formula
- Reiterate the importance of identifying sides and heights correctly