NCERT Solutions for Class 4 Maths Chapter 1 - Building With Bricks

Missing Question 1: Which pattern do you like the most?

Ans:

We can make as many brick patterns as shown in the picture. 

I would like the bricks which will make the shape of a dome which is in the pattern $5$.

Missing Question 2: Have you seen these patterns anywhere?

Ans:

Yes. I have seen these patterns.

Once I went to an old mosque. I have seen these brick patterns there.

Question 1:

Which Pattern is made in a circle?

Ans:

By observing the above given patterns, I observe that pattern J is made in a circle.

In which pattern can you show mirror halves?

Ans:

Mirror halves objects are those in which the objects are the same in both sides of the symmetry line. 

Hence draw the symmetry line through the center of the object and see if we obtain mirror halves.

Hence the mirror halves can be shown in $5$patterns. They are $\text{A, B, H, I, J}$.

The line can be drawn to show the mirror halves as shown below:

Question 2:

How many faces does a brick have?

Ans:

Generally the brick will be in the shape of a cuboid. So every brick has $6$ faces.

Is any face a square?

Ans:

We know that the brick is of cuboid shape.

The cuboid is formed of six rectangular faces.

So there is no square face in cuboid.

Draw the smallest face of the brick.

Ans:

The smallest side of the brick is the side with a breadth and height and it can be drawn as follows:

Question 3:

Which are the faces of a brick? Mark a $\left(  \right)$.

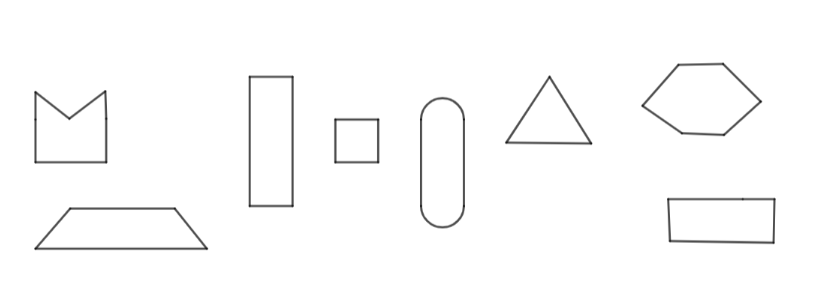
Ans:

A brick is of the shape of a cuboid of cube. 

Thus the shape of the brick consists of a rectangle and square. 

So insert the $\left(  \right)$ symbol in the shape of rectangle and square.

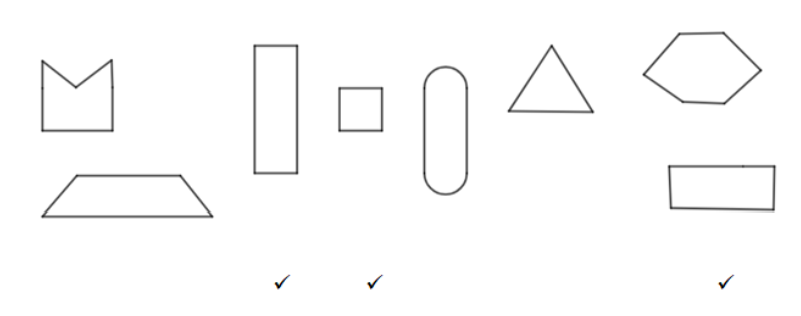
These are the shapes of squares and rectangles which can make the faces of bricks.

Question 4:

Which of these is a drawing of a brick? Mark a ($$).

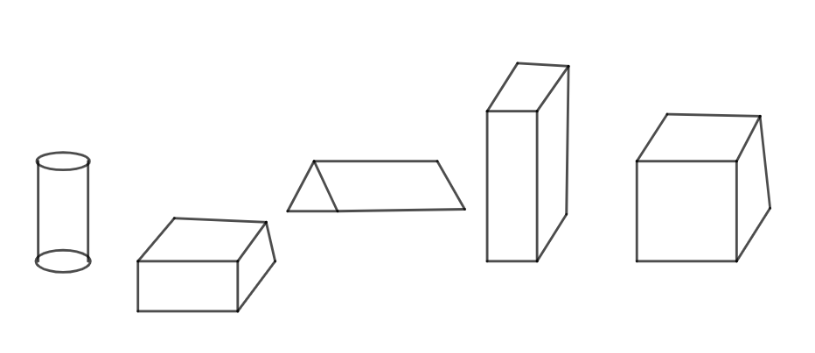
Ans:

The brick is in the shape of a cuboid. 

So from the diagram, the shape of the cuboid is found.

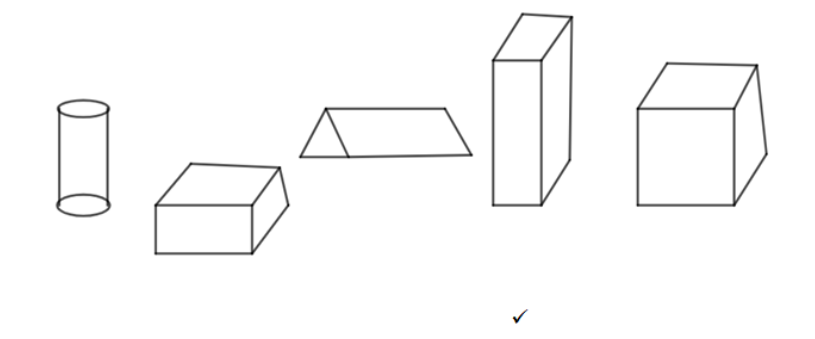
Hence the shape of the cuboid has been ticked.

Question 5:

Make a drawing of this box to show three of its faces.

Ans:

To draw the box with three faces, just flip the box and we obtain the box with three faces.

Hence this box diagram with three faces has been drawn.

Question 6:

Can you make a drawing of a brick which shows $4$ of its faces?

Ans:

The brick is a 3D shape of cuboid.

And so it is impossible to show the $4$ faces of the brick in a sheet of paper.

Missing Question 3:

What do you think? Which wall will be stronger?

Ans:

Zainab did not interlock the brick pattern. 

But Muniya places her bricks in an interlocking pattern. 

So the walls of Muniya will be stronger since her bricks are tightly packed with each other.

Question 7:

Different Wall patterns:

Here are photos of three kinds of brick walls. Can you see the difference in the way the bricks are placed?

Ans:

Observe the patterns.

The brick in the first picture has one brick horizontally placed between the two vertical placed bricks.

The bricks in the third picture are more tightly packed than that of bricks in the second picture.

Now match the photo of each wall with the correct drawing below:

Ans:

As described in the above question, match the bricks with the interlocking patterns in the patterns given in this question.

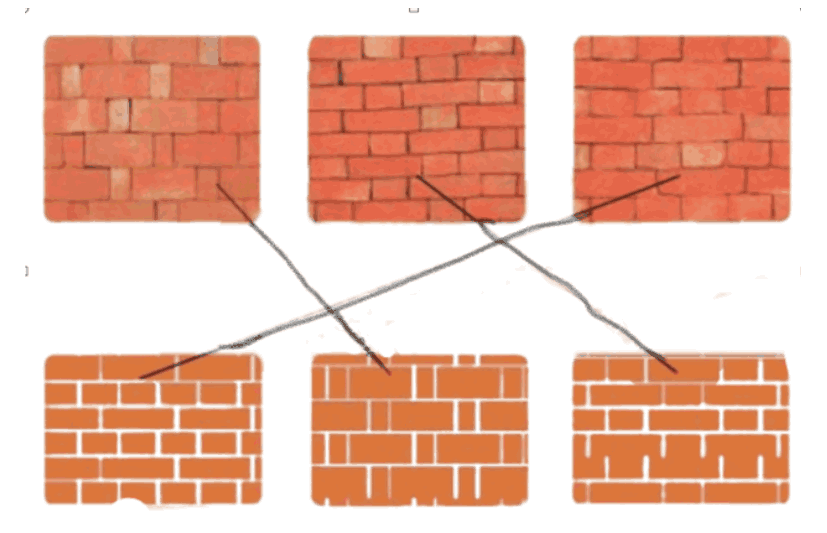
Hence the bricks have been matched with its pattern.

Question 8:

How many different ‘jaali’ patterns can you see in these two photos?

Ans:

The above building seems to have five different ‘Jaali’ patterns.

The pillar is made of one pattern. 

The walls of building made of one pattern, 

The upper layer of the balcony is made of one pattern.

The balcony layer with designs made of one pattern.

And the above floor with design on both sides made of one pattern.

So five patterns of “Jaali” are there in the above building.

Question 9:

Now color some bricks red and make your own ‘jaali’ patterns in the wall drawn below.

Ans:

To make our own ‘jaali’ pattern, we can choose any side of the above given ‘jaali’ pattern.

Our ‘jaali’ pattern is made in the center with some designs on the wall.

Question 10:

Now draw some jharokha patterns on the wall here. You can shade it black.

Ans:

The Jharoka is a stone window that is projecting from the wall of the building.

To draw the jharokha pattern and shade them in black:

Hence the wall with jharokha pattern has been drawn.

Question 11:

Where else have you see an arch?----------------------------------

Ans:

An arch is a typically curved structure that will function as an opening and provide structural support.

It can be seen in many places.

But I have seen the arch in the bridges, the rainbow and so on.

Question 12:

Which of these bricks have curved edges?

Ans:

Curved edges refer to the edges that are rounded in the edges.

So observe the rounded edge of the bricks from the diagram.

The bricks in the left corner have the curved edge and the image of that brick is given:

How many do you see of the longest brick?

Ans:

The longest brick is in the front side.

Only two of six faces are observed by me.

Thus only two faces of the longest brick are seen.

Is there any brick which has more than six faces?

Ans:

Generally bricks are of cuboid shape and consist of only six faces. 

So bricks cannot have more than six faces.

Question 13:

Take one brick and measure it.

(a) How long is it? ---------------------------

Ans:

Take a brick.

Measure the length of the brick with the ruler.

The length of the brick is about $\text{20 cm}$.

(b) How wide is it?

Ans:

Take a brick.

Measure the width of the brick with the ruler.

The width of the brick is about $\text{8 cm}$.

(c) How high is it?

Ans:

Take a brick.

Measure the height of the brick with the ruler.

The height of the brick is about $\text{1 cm}$.

Question 14:

Muniya wants to make a wall $1$ meter long. How many bricks will she need to put in a line?

Ans:

Consider the length of the brick to be $\text{20 cm}$

Muniya needs to build a wall of $\text{1 m}$

We know that $\text{1 m=100 cm}$

We need $n$ number of bricks of $\text{20 cm}$ to build a $\text{100 cm}$ wall.

Thus, $20n=100$

              $n=\frac{100}{20}$

              $n=5$

Hence $5$ bricks are required to build a wall of $\text{1m}$in a line.

Question 15:

Can you guess how high the chimney is here? Is it: 

(a) about 5 meters

(b) about $15$ meters

(c) about $50$ meters

Ans:

We know that the length of the brick is about $20\text{ cm}$.

From the height of the chimney, we know that the height of the chimney is very high.

So we can conclude that the chimney is about $50$ meters tall.

Question 16:

Here are four pictures from the brick kiln. These pictures are jumbled up. Look at them carefully. Write the correct order.

Ans:

The bricks are made from the following process,

• Collecting the mud

• Made mud into small parts.

• Separate the mud leaving some spaces between them.

• Finally arranging them one above the other.

The order given above follows.

Thus the correct sequence of the picture form brick is $\text{C, D, B, A}$

Question 17:

Mental Math: Bhajan buys Bricks. Bhajan went to buy bricks. The price was given for one thousand bricks. The prices were also different for different types of bricks.

Bhajan decided to buy the new bricks from Brickabad. He bought three thousand bricks. How much did he pay?

Ans:

Since Bhajan decided to buy bricks from Brickabad, 

Cost of one thousand bricks $=Rs.2000$

Cost of $3$thousand bricks $=3\times 2000$

$=Rs.6000$

The cost of three thousand bricks from Brickabad is $Rs.6000$

Guess what he will pay if he buys $500$ bricks.

Ans:

Bhajan buys $500$ old bricks in this case.

Cost of $1000$bricks $=Rs.1200$

Cost of $500$ bricks $=\frac{1200}{2}$

$=Rs.600$

Thus the cost of $500$ old bricks is $Rs.600$.

Conclusion

NCERT Solutions for Class 4 Math Chapter 1 Building with Bricks by Vedantu provides a fun and engaging way for students to learn about patterns, shapes, and spatial understanding using bricks as a visual aid. They provide a comprehensive and detailed explanation of the concepts, making it easier for students to understand and apply them. This chapter helps children recognize and create different patterns, understand symmetry, and improve their observation skills. It's important for students to focus on identifying various patterns and practising drawing them, as this will enhance their ability to visualize and solve problems creatively.

Other Related Links for CBSE Class 4 Maths Chapter 1

Chapter-Specific NCERT Solutions for Class 4 Maths

Given below are the chapter-wise NCERT Solutions for Class 4 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

CBSE Class 4 Maths Study Materials