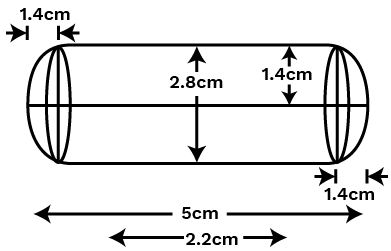
Master Surface Area And Volume Class 10 With Vedantu's Expert Solutions
NCERT Solutions For Class 10 Maths Chapter 12 Surface Area And Volume
FAQs on NCERT Solutions For Class 10 Maths Chapter 12 Surface Area And Volume
1. Where can I find stepwise NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.2 as per the CBSE 2025–26 syllabus?
You can access the complete, stepwise NCERT Solutions for Class 10 Maths Chapter 12 Exercise 12.2 following the latest CBSE 2025–26 pattern directly on this page. All solutions use official NCERT methods and provide each answer in a clear, easy-to-understand NCERT answer format, making them ideal for CBSE exam preparation.
2. What is the correct NCERT-approved method to solve problems on surface area and volume in Class 10 Maths Chapter 12?
To solve surface area and volume problems in Class 10 Maths Chapter 12, begin by identifying the correct solid figure (cube, cuboid, cylinder, cone, sphere, or combinations). Use the standard NCERT formulas given for Total Surface Area, Lateral Surface Area, and Volume as specified in the textbook. Remember to show all calculation steps as per CBSE marking scheme and present your answer in the proper NCERT structure.
3. How can I get NCERT Solutions for Class 10 Maths Chapter 12 in Hindi medium?
Updated NCERT Solutions for Class 10 Maths Chapter 12, including Hindi medium versions for exercises 12.1, 12.2, and 12.3, are available in a textbook-accurate answer format. Each step is translated and explained in Hindi, strictly as per CBSE and NCERT guidelines for 2025–26.
4. Are these Class 10 Maths Chapter 12 NCERT solutions valid for CBSE board exams in 2025–26?
Yes, all NCERT Solutions for Class 10 Maths Chapter 12 provided here follow the officially updated CBSE 2025–26 syllabus. Answers are prepared strictly according to the current NCERT textbook and CBSE board exam marking scheme for maximum exam accuracy.
5. How do I solve Exercise 12.1 of Chapter 12 Surface Area and Volume using the NCERT stepwise format?
To solve Exercise 12.1 of Class 10 Maths Chapter 12 Surface Area and Volume, carefully read each question and identify the shape involved. Apply the respective formula for surface area or volume as listed in your NCERT textbook. Present every calculation and reasoning step clearly, adhering to CBSE 2025–26 guidelines for stepwise marks and use accurate units in the final answer.
6. Can I download a free PDF of NCERT Solutions for Class 10 Maths Chapter 12 Surface Area and Volume?
Yes, you can download the free PDF of NCERT Solutions for Class 10 Maths Chapter 12 Surface Area and Volume with detailed stepwise explanations. The PDF is based on the updated CBSE syllabus, and all answers are presented following the NCERT pattern for each exercise.
7. Where can I find the textbook answer key for Class 10 Maths Chapter 12 Exercise 12.3?
The official answer key for Class 10 Maths Chapter 12 Exercise 12.3 follows the NCERT textbook format and CBSE-approved solution method. All questions have detailed solutions with stepwise explanations and are available for both English and Hindi medium students as per the 2025–26 exam requirements.
8. What is the recommended stepwise approach for mixed solid questions in Class 10 Maths Chapter 12 NCERT?
For mixed solid questions in Chapter 12 of the Class 10 Maths NCERT book, first break down the figure into familiar base shapes (like cylinder, cone, or hemisphere). Use the specific NCERT surface area or volume formula for each component, calculate separately, then add (or subtract, if required) as per the question. Ensure each calculation is shown stepwise for full CBSE marks.
9. Do the NCERT Solutions for Class 10 Maths Chapter 12 provided here use the 2025–26 prescribed CBSE answer format?
All solutions for Class 10 Maths Chapter 12 Surface Area and Volume on this page adhere strictly to the CBSE 2025–26 prescribed answer format. Stepwise explanations, units, correct formula application, and detailed reasoning are included to match current board requirements.
10. How do I avoid common mistakes while answering NCERT intext questions in Chapter 12 Surface Area and Volume?
To avoid mistakes in NCERT intext questions for Chapter 12, always write the correct formula with units before substituting values. Clearly distinguish between surface area and volume questions, double-check conversions (especially with cm, m, and mm), show every calculation step as per CBSE guidelines, and box the final answer using the NCERT answer key style.
11. What is the difference between Total Surface Area and Curved Surface Area, and how should I present these in NCERT Solutions?
Total Surface Area (TSA) of a solid is the sum of all its faces or curved surfaces, while Curved Surface Area (CSA) includes only the area of curved parts, excluding bases or flat surfaces. In NCERT Solutions, explicitly write which formula is being used for TSA or CSA, show all substitution steps, and clearly define each term according to the official NCERT answer format to maximize marks.
12. Can I refer to these NCERT Solutions for competitive exams like NTSE or Olympiads besides CBSE board exams?
Yes, these NCERT Solutions for Class 10 Maths Chapter 12 Surface Area and Volume are based completely on the NCERT textbook, making them a reliable reference for CBSE board exams, NTSE, and other competitive exams that follow the NCERT syllabus. The stepwise, logical approach helps in building strong conceptual foundations for all exam formats.
13. Why are units and final answer formatting important in NCERT Solutions for Maths Chapter 12?
Using correct units (cm2, m3, etc.) and formatting the final answer clearly as per the NCERT pattern ensures full marks in CBSE exams. It also avoids confusion when checking answers and demonstrates a proper CBSE-approved solution that examiners expect in 2025–26.




















 Watch Video
Watch Video