What are Compound Angles?

Simply put, trigonometric functions—also called circular functions—are the functions of a triangle's angle. This means that these trigonometric functions provide the relationship between the angles and sides of a triangle. The fundamental trigonometric functions are sine, cosine, tangent, cotangent, secant, and cosecant.

We need to know trigonometric ratios to get a clear view of the compound angles.

Angles

An angle is created when two rays are united at a common point. The two rays are referred to as the arms of the angle, while the common point is the node or vertex. The symbol "$\pi$” stands for the angle. The Latin word "Angulus" is where the word "angle" originated.

Typically, an angle is measured with a protractor and expressed in degrees. Here, several angles are shown at 30 degrees, 45 degrees, 60 degrees, 90 degrees, and 180 degrees. The angles' degrees values determine the many types of angles.

Angles can be expressed in terms of pi ($\pi$) or radians.

Trigonometric Ratios

The ratios of the triangle's side lengths are known as trigonometric ratios. These ratios explain how the ratio of a right triangle's sides to each angle works in trigonometry. The sin, cos, and tan functions can obtain the other significant trigonometric ratios, cosec, sec, and cot.

Trigon, which means "triangle," and metrôn, which means "to measure," are the roots of the term "trigonometry." It is a field of mathematics that examines how a right-angled triangle's angles and sides relate to one another.

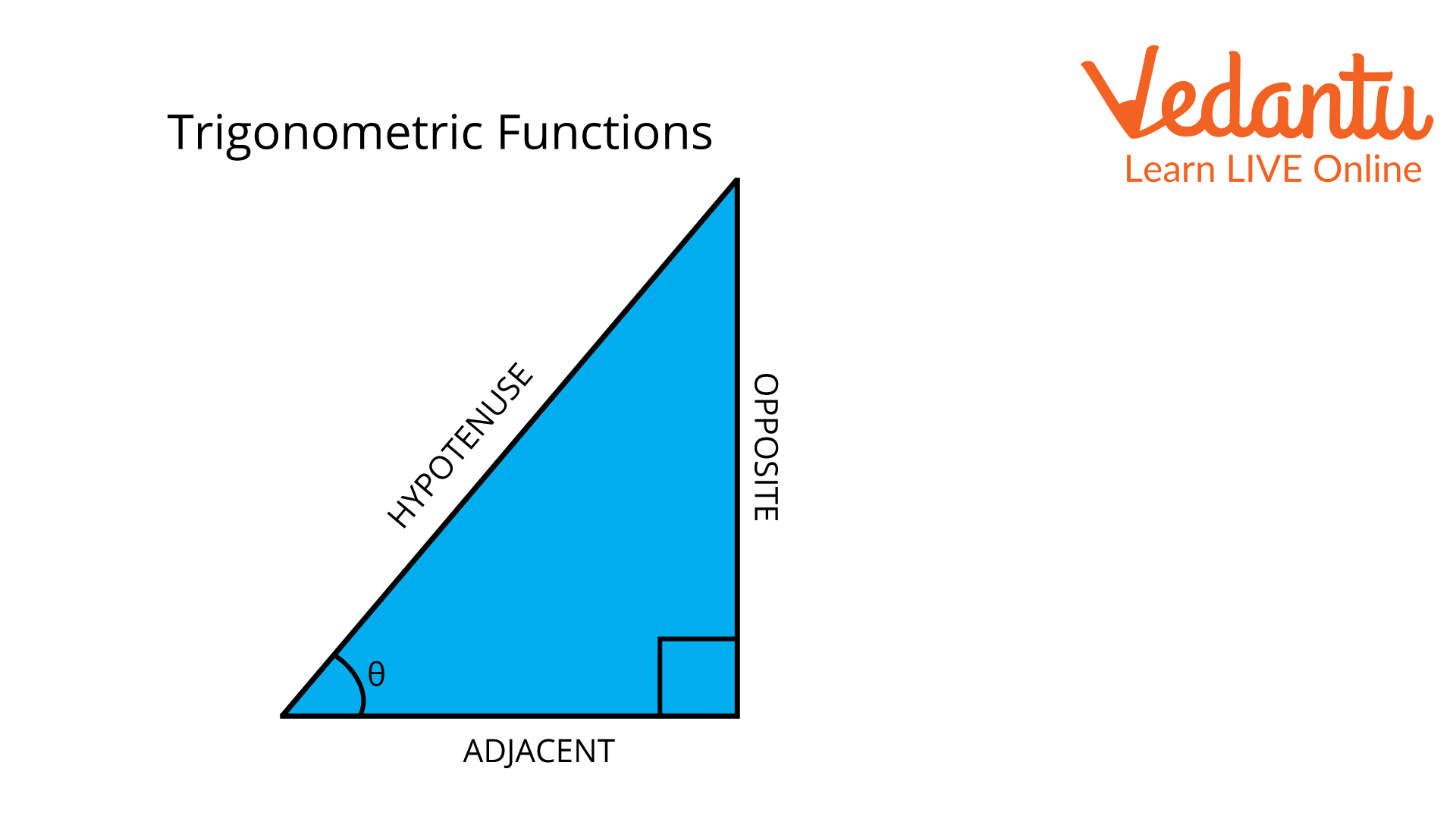
Trigonometric Functions

Trigonometric Identities

Trigonometric Identities come in handy whenever trigonometric functions are incorporated into an expression or equation. For every value of a variable appearing on both sides of an equation, a trigonometric identity is true. These trigonometric identities involve one or more angles' sine, cosine, and tangent.

What are Compound Angles?

An algebraic sum of two or more angles can define the compound angle. Compound angles represent different trigonometric identities.

Compound angles are denoted using trigonometric identities. Compound angles can be used to compute the fundamental operations of finding the sum and difference of functions.

Formula of Compound Angles

The formula for trigonometric ratios of compound angles is given below:

• $\sin {\rm{ }}(A + B){\rm{ }} = \sin {\rm{ }}A{\rm{ }}\cos {\rm{ }}B{\rm{ }} + \cos {\rm{ }}A{\rm{ }}\sin {\rm{ }}B$

• $\sin \left( {A - B} \right) = \sin A\cos B - \cos A\sin B$

• $\cos {\rm{ }}(A + B){\rm{ }} = \cos {\rm{ }}A{\rm{ }}\cos {\rm{ }}B - \sin {\rm{ }}A{\rm{ }}\sin {\rm{ }}B{\rm{ }}$

• $\cos {\rm{ }}(A - B){\rm{ }} = \cos {\rm{ }}A{\rm{ }}\cos {\rm{ }}B{\rm{ }} + \sin {\rm{ }}A{\rm{ }}\cos {\rm{ }}B{\rm{ }}$

• $\tan \left( {A + B} \right) = \dfrac{{\tan A + \tan B}}{{1 - \tan A\tan B}}$

• $\tan \left( {A - B} \right) = \dfrac{{\tan A - \tan B}}{{1 + \tan A\tan B}}$

• $\sin (A + B)\sin \left( {A - B} \right) = {\sin ^2}A - {\sin ^2}B = {\cos ^2}B - {\cos ^2}A$

• $\cos \left( {A + B} \right)\cos \left( {A - B} \right) = {\cos ^2}A - {\sin ^2}A - {\sin ^2}B = {\cos ^2}B - {\sin ^2}A$

Questions on Compound Angles

Question 1: If $\cos A = \dfrac{4}{5}$ and $\cos B = \dfrac{{12}}{{13}},\dfrac{{3\pi }}{2} < A,B < 2\pi$, find the value of $\cos (A+B) $.

Solution:

According to the given question, $\cos A = \dfrac{4}{5}$ and $\cos B = \dfrac{{12}}{{13}}$. Also, $\dfrac{{3\pi }}{2} < A,B < 2\pi$, both A and B lie in the fourth quadrant. Then we can say that both sin A and sin B are negative.

First we need to find out $\sin A$,

$\begin{array}{c}\sin A = - \sqrt {1 + {{\cos }^2}A} \\ = - \sqrt {1 - \dfrac{{16}}{{25}}} \\ = - \dfrac{3}{5}\end{array}$

We need to find out $\sin B$,

$\begin{array}{c}\sin B = - \sqrt {1 + {{\cos }^2}B} \\ = - \sqrt {1 - \dfrac{{144}}{{169}}} \\ = - \dfrac{5}{{13}}\end{array}$

Now, we can find out $\cos (A+B)$,

$\begin{array}{c}\cos (A + B) = \cos A\cos B - \sin A\sin B\\ = \dfrac{4}{5} \times \dfrac{{12}}{{13}} - \left( {\dfrac{{ - 3}}{5}} \right) \times \left( {\dfrac{{ - 5}}{{13}}} \right)\\ = \dfrac{{48}}{{65}} - \dfrac{{15}}{{65}}\\ = \dfrac{{33}}{{65}}\end{array}$

Question 2: Determine the value of $\sin {15^\circ }$.

Solution:

According to the given question, we need to find the value of $\sin {15^\circ }$.

$\sin \left( {A - B} \right) = \sin A\cos B - \cos A\sin B$

$\sin \left( {45 - 30} \right) = \sin 45\cos 30 - \cos 45\sin 30$

$\begin{array}{c}\sin {15^ \circ } = \dfrac{1}{{\sqrt 2 }} \times \dfrac{{\sqrt 3 }}{2} - \dfrac{1}{{\sqrt 2 }} \times \dfrac{1}{2}\\ = \dfrac{{\sqrt 3 - 1}}{{2\sqrt 2 }}\end{array}$

Question 3: If A, B, and C are angles of a triangle, then prove that $\dfrac{A}{2} = \cot \left( {B + C} \right)/2$.

Solution:

According to the given question, we know A, B, and C are the angles of a triangle,

$\begin{array}{l}A + B + C = n\\B + C = n - A\\\dfrac{{\left( {B + C} \right)}}{2} = \dfrac{n}{2} - \dfrac{A}{2}\end{array}$

Then,

$\begin{array}{l}\cot \dfrac{{\left( {B + C} \right)}}{2} = \cot \left( {\dfrac{n}{2} - \dfrac{A}{2}} \right)\\ = \tan \dfrac{A}{2}\end{array}$

Hence, proved.

Conclusion:

Trigonometry was developed to solve problems and take measurements involving triangles. Trigonometry is a tool used by meteorologists, engineers, scientists, engineers, engineers, engineers, and navigators. It is referred to as sum and difference formulas in American mathematics, but it is known as compound angles in British Mathematics. Trigonometric functions are utilised to obtain consistent results, including compound angles, trigonometric ratios, and multiple angles.