Introduction to Multiple Angles
Have you ever thought about which branch of Mathematics deals with multiple angles? Multiple angles are widely used in a Mathematics branch named Trigonometry. Let A be a given angle, then 2A, 3A, 4A, etc., are called multiple angles. The multiple angles topic comes under the trigonometric functions. It is not possible to find the values of multiple angles directly. We can calculate the values of multiple angles by expressing each trigonometric function in its expanded form using multiple-angle formulas.
Learning the trigonometric multiple angles formula helps students to save time while solving problems. Every student should know it is one of the most common advanced mathematics topics.
What are Multiple Angles?
The integral multiple of the angles of a triangle is called multiple angles. For example, if A be the angle of a triangle, then the multiple angles of A are given by multiplying the angle A with the natural numbers, such as 2A, 3A, 4A, etc. The trigonometric functions often appear with multiple angles. It is impossible to find their values directly, but their values can be evaluated by expressing each trigonometric function in its expanded form. These angles form a part of the trigonometric functions.
For example,
Show that $\dfrac{\left(3 \sin A-4 \sin ^3 A\right) }{\left(4 \cos ^3 A-3 \cos A\right)}=\tan 3 A$ by using the multiple angle formula.
Ans: We have multiple angle formulas $\sin 3 A=3 \sin A-4 \sin ^3 A$
$\cos 3 A=4 \cos ^3 A-3 \cos A$
$\dfrac{\left(3 \sin A-4 \sin ^3 A\right)}{\left(4 \cos ^3 A-3 \cos A\right)}=\dfrac{\sin 3 A}{\cos 3 A}$
$=\tan 3 A$
Here, we can say that by using the concept of multiple angle formula, we can easily solve the trigonometric problems.
Multiple Angle Formula
The multiple angle formula depicts the formula used to calculate multiple angles. The simplest and most widely used method to obtain multiple angles is by using trigonometric identities.
The sin formula for multiple angles is:
$\sin n \theta=\sum_{k=0}^n \cos ^k \theta \sin ^{n-k} \theta \sin \left(\dfrac{1}{2}(n-k)\right) \pi$
The multiple angles Cosine formula is:
$\cos n \theta=\sum_{k=0}^n \cos ^k \theta \sin ^{n-k} \theta \cos \left(\dfrac{1}{2}(n-k) \pi\right)$
Tangent multiple angles formula is:
$\operatorname{Tan} \mathrm{n} \theta=\dfrac{\sin \mathrm{n} \theta}{\cos n \theta}$
Now, learn how to expand trigonometric functions with multiple angles.
Solved Examples
Q 1. To show that cos 5x = 16 cos5x - 20 cos3x + 5 cos x.
Ans: This is proved by taking into account LHS and proving it equal to RHS, i.e.
L.H.S $=\cos 5 x$
Decomposing $5 x$ to $3 x$ and $2 x$, we get,
$=\cos (2 x+3 x) \quad-1$
$\cos (A+B)=\cos A \cos B-\sin A \sin B$
$\cos 2 A=2 \cos ^2 A-1$
$\cos 3 A=4 \cos ^3 A-3 \cos A$
$\sin 2 A=2 \sin A \cos A$
$\sin 3 A=3 \sin A-4 \sin ^3 A$
Using the above formulas in equation 1, we get,
$=\cos 2 x \cos 3 x-\sin 2 x \sin 3 x$
$=\left(2 \cos ^2 x-1\right)\left(4 \cos ^3 x-3 \cos x\right)-2 \sin x \cos x\left(3 \sin x-4 \sin ^3 x\right)$
$=8 \cos ^5 x-10 \cos ^3 x+3 \cos x-6 \cos x \sin ^2 x+8 \cos x \sin ^4 x$
$=8 \cos ^5 x-10 \cos ^3 x+3 \cos x-6\left(1-\cos ^2 x\right) \cos x+8\left(1-\cos ^2 x\right)^2 \cos x$
$=8 \cos ^5 x-10 \cos ^3 x+3 \cos x+\left[-6 \cos x+6 \cos ^3 x+8 \cos x\left(1+\cos ^4 x-2 \cos ^2 x\right)\right]$
$=8 \cos ^5 x-10 \cos ^3 x+3 \cos x-6 \cos x+6 \cos ^3 x+8 \cos x+8 \cos ^5 x-16 \cos ^3 x$
$=16 \cos ^5 x-20 \cos ^3 x+5 \cos x$
$=\text { R.H.S }$
Hence Proved.
Thus, the value of $\cos 5 x=16 \cos ^5 x-20 \cos ^3 x+5 \cos x$.
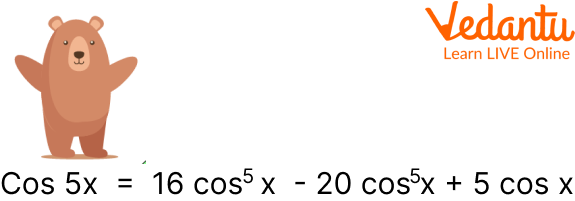
The Multiple Angles Trigonometric Example
Practice Problems
Q 1. Show that $\dfrac{\sin 2x + \sin x}{\cos 2x + 1 + \cos x}= \tan x$
Q 2. Show that sin 4x = 4 cos3x sin x - 4 cosx sin3x
Q 3. Show that sin 5x = 5 cos4x sin x - 10 cos2x sin3x+ sin5x
Multiple Angles Worksheet
Worksheets for multiple angles are given to help students in mastering the concept.
Q 1. Show that $\cos 4x = \cos ^4 x - 6 \cos^2x \sin^2 x + \sin ^4x$
Q 2. Show that $\tan 4x = \dfrac{4 \tan x - 4 \tan^3 x}{1 - 6 \tan^2x + \tan ^4x}$
Q 3. Show that $\tan 3x = \dfrac{3 \tan x - \tan^3 x}{1 - 3 \tan^2x}$
Q 4. Evaluate the following in terms of tan:
(i) sin 8A
(ii) cos 6A
Summary
Finishing up here with the concept of multiple angles and the trigonometric multiple angles formulas. Every subject in this article has been examined in an easy language and eye-catching format to better understand the concepts. Images are also used to make the understanding of the topic interesting. Some solved examples and practice problems are also discussed to make students master the given topics easily. Hoping you enjoyed learning the topic.
FAQs on Multiple Angles
1. What is trigonometry?
Trigonometry is defined as the branch of Mathematics that deals with the sides and angles of a triangle. It is mostly used on the right triangle, i.e. one angle is 90 degrees. It is used to express the relationship between the sides and angles of a triangle. There are six trigonometric ratios namely; sin θ, cos θ, tan θ, cosec θ, sec θ, and cot θ.
2. Define a straight line.
A straight line is defined as a one-dimensional figure that has neither width nor height. It has zero curvature. Two points are required to denote a line.
3. What are the different types of angles?
There are six different types of angles, whose names are given below:
1. Acute Angle: An angle which is less than $90^{\circ}$.
2. Right Angle: An angle whose measure is $90^{\circ}$.
3. Obtuse Angle: An angle which is more than $90^{\circ}$ and less than $180^{\circ}$.
4. Straight Angle: An angle whose measure is $180^{\circ}$.
5. Reflex Angle: An angle which is more than $180^{\circ}$ and less than $360^{\circ}$.
6. Complete Angle: An angle whose measure is $360^{\circ}$.
