Radian Measure

Radian Measure was introduced to relate the concept of measure of angle with the radius of a circle. The main benefit of radians is that we can represent radian measures with the help of real numbers. A circle is made up of \[2\pi \] radians, where one radian is equal to \[\dfrac{1}{6}\] of a circle approximately. The total angle of a circle in degrees is equal to \[{360^ \circ }\]. Hence, \[2\pi rad = {360^ \circ }\].

Definition of Radian Measure

Given a circle of radius one unit, consider an arc of length one unit. The angle subtended by the arc at the center of the circle is one radian. So, Radian Measure is a unit of measure of the angle.

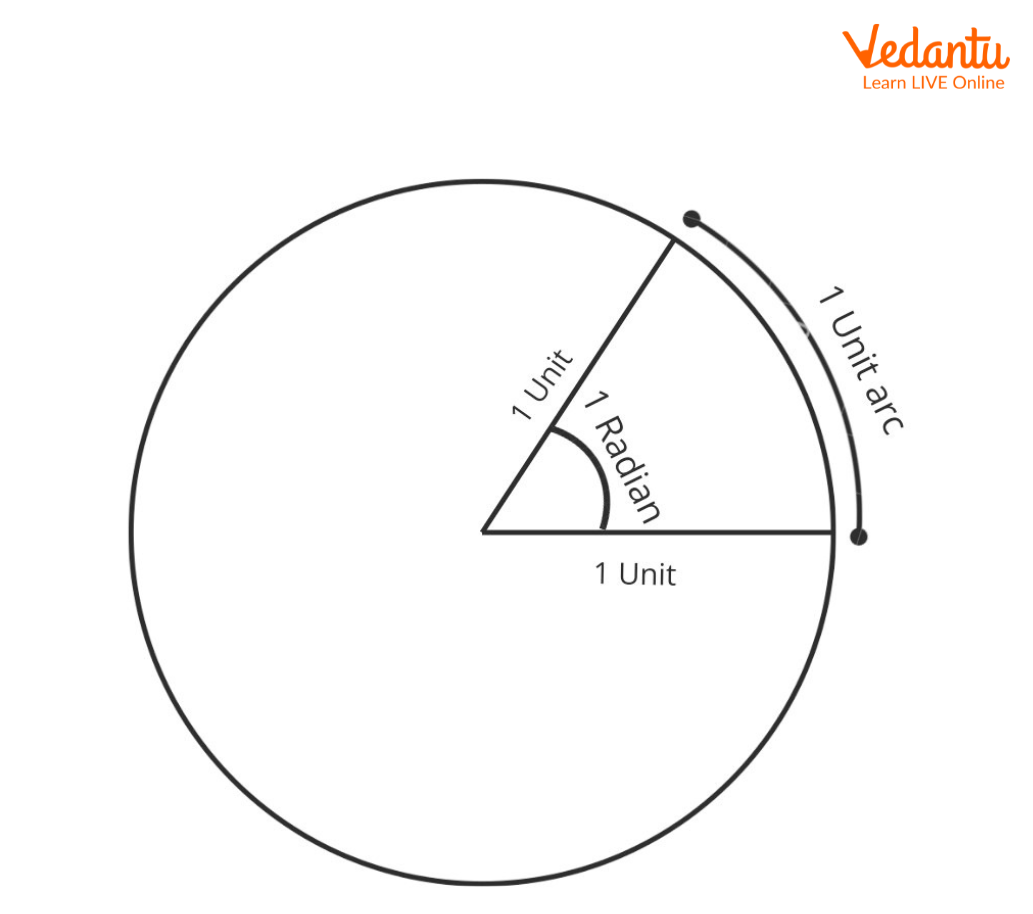
Definition of Radian Measure

Mathematically, we can write:

Symbol of Radian Measure

The symbol of Radian Measure is rad or c.

Radian Measure Formula:

The formula for finding Angle subtended by Arc at the centre of circle in Radian Measure for given length of arc and radius of the circle is:

\[{\rm{Angle}}\left( {{\rm{Radian\;Measure}}} \right) = {\rm{\theta }} = \dfrac{{\text{Length of arc}}}{{\text{Radius}}} = \dfrac{l}{r}\] \[ = > l = r\theta \]

For example, Given Length of Arc l=2cm and the Radius of Circle r=1 cm, the Angle subtended by the Arc at the centre of circle is given by:

\[{\rm{Angle}}\left( {{\rm{Radian\;Measure}}} \right) = {\rm{\theta }} = \dfrac{{\text{Length of arc}}}{{\text{Radius}}} = \dfrac{l}{r}\]

\[\begin{array}{l} = \dfrac{{2cm}}{{1cm}}\\ = 1(R.M)\end{array}\]

Relation Between Radian Measure and Real Numbers

Every Real Number corresponds to the radian measure of some angle subtended by the arc at the centre of the circle.

Consider a circle centered O with a unit radius and consider a point A on the circumference of the circle. Draw a tangent to the circle at point A. Label this as line m, a line representing real numbers. Let the zero of the line m be at point A. Consider two points P and Q on opposite sides of point A.

Take a thread and measure the distance AP and cut it out, then, starting from A, start placing the cutting of the thread along the circumference of the circle in an Anti-Clockwise direction. Label this point as\[{\rm P}'\].Similarly, measure the same distance along the negative axis (\[AP = AQ\]). Now, take that thread and place it along the circumference of the circle in a Clockwise direction. Label that point as \[Q'\].

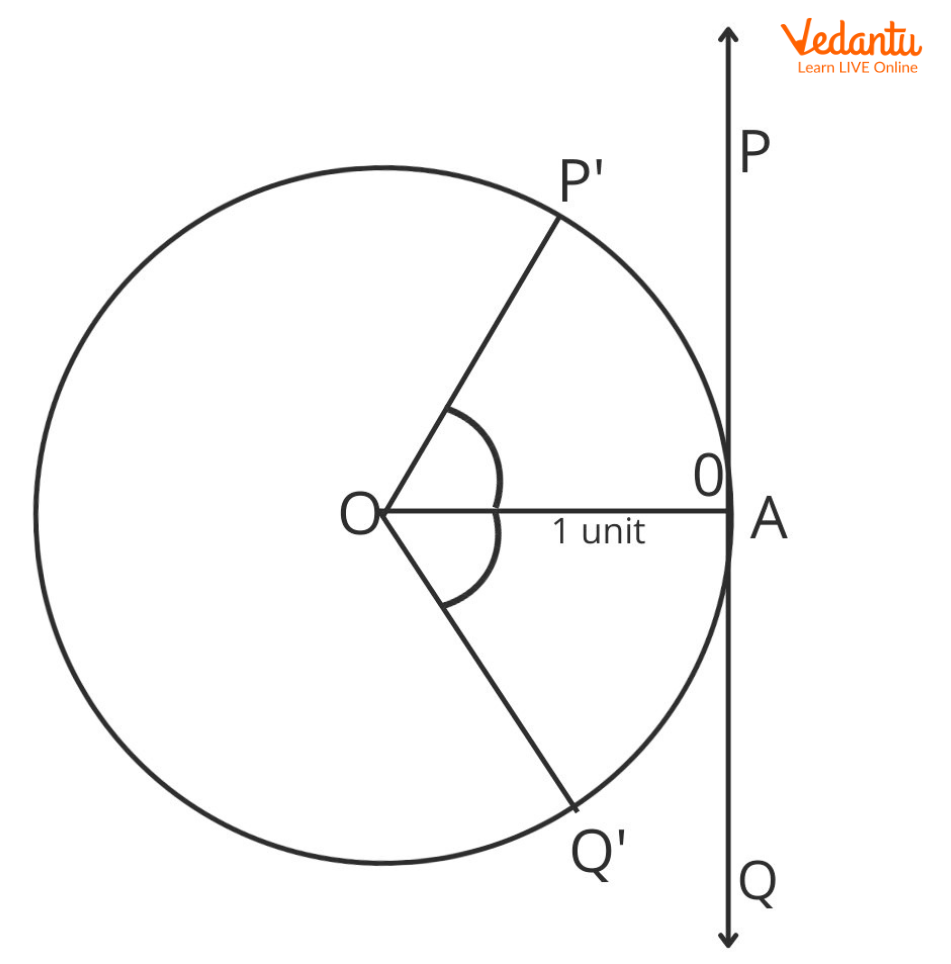
Radian Measure and Real Numbers

Here,\[AP = AQ\].

Through our construction,

Let \[\begin{array}{l}\angle AOP' = {\theta _1}\\\angle AOQ' = {\theta _2}\end{array}\]

Using Definition of angle, arc and radian.

So the lengths of arcs are related to the measure of the angle in radians and the values on the real line are equal to the lengths of arcs on the circle, we see that every real number corresponds to Radian Measure.

Relation Between Radian Measure and Degree Measure:

We know that a circle subtends a 360° angle at the center and its radian measure is 2π, so, 2π rad = 360°, which means π rad = 180°. Since value of π is \[\dfrac{{22}}{7}\], so

\[1rad=\dfrac{{180^{\circ}}}{\pi} = \dfrac{{180^{\circ }}}{\dfrac{22}{7}} = 57^{\circ} 16'\](approx.)

Now, \[1^\circ = \dfrac{\pi }{{180^\circ }} = 0.01746rad\](approx.)

So, the formulas for conversion of Degree Measure to Radian Measure and vice-versa are:

\[R.M = \dfrac{\pi }{{{{180}^ \circ }}} \times D.M.\]

and

\[D.M = \dfrac{{180^\circ }}{\pi } \times R.M.\]

Some Standard Angle Conversions

1 Radian is Equal To?

We know that

\[D.M = \dfrac{{180^\circ }}{\pi } \times R.M.\]

Given \[R.M. = 1\]

So, \[D.M. = \dfrac{{{{180}^ \circ }}}{\pi } \times 3 = \dfrac{{180^\circ }}{{\dfrac{{22}}{7}}} \times 3\]

\[ = \dfrac{{180^\circ }}{{22}} \times 7 \times 1 = \dfrac{{1260^\circ }}{{22}} = 57{\textstyle{3 \over {11}}}^\circ \]

As \[1^\circ = 60\min \],so,

\[\begin{array}{l}D.M. = 57^\circ + {\textstyle{3 \over {11}}}^\circ \\ = 57^\circ + ({\textstyle{3 \over {11}}}) \times 60'\\ = 57^\circ + ({\textstyle{{180} \over {11}}})'\\ = 57^\circ + 16{\textstyle{4 \over {11}}}'\\ = 57^\circ + 16' + {\textstyle{4 \over {11}}}'\end{array}\]

As \[1\min = 60\sec \],so,

\[\begin{array}{l}D.M. = 57^\circ + 16' + {\textstyle{4 \over {11}}} \times 60''\\ = 57^\circ + 16' + {\textstyle{{240} \over {11}}}''\\ = 57^\circ + 16' + 21.81''\\ \simeq 57^\circ 16'22''\end{array}\]

Hence, \[D.M.\]\[ = 57^\circ 16'22''\]

So, 1 rad is 57 degrees 16 minutes and 22 seconds.

Uses of Radian Measure:

• Radian Measure relates Algebra to Trigonometry.

• The trigonometric functions have simpler forms of derivatives when the angle is in Radian Measure. Otherwise, you will have to multiply a factor of \[{\textstyle{\pi \over {180}}}\]every time you need to find the derivative of such functions.

• Since Radian Measure is connected to real numbers, we can easily represent any angle in form of a real numbered value.

Interesting Facts

• There are about 6.28 radians in a complete revolution.

• The Right angle is \[\dfrac{\pi }{2}\]rad.

• The straight line is \[\pi\] rad.

• We can use Radian Measure to find the length of the arc, area, and circumference of the sector made by the arc.

• Length of arc \[l = r\theta \].

• Area of sector made by Arc \[a = {\textstyle{1 \over 2}}{r^2}\theta \].

• Perimeter of sector made by Arc \[p = l + 2r = r\theta + 2r = r(\theta + 2)\].

Radian Measure Examples With Solutions:

1. Convert 3 radians into Degree Measure.

Ans: We know that\[D.M = \dfrac{{180^\circ }}{\pi } \times R.M.\]

Given \[R.M. = 3\]

So, \[D.M. = \dfrac{{{{180}^ \circ }}}{\pi } \times 3 = \dfrac{{180^\circ }}{{\dfrac{{22}}{7}}} \times 3\]

\[ = \dfrac{{180^\circ }}{{22}} \times 7 \times 3 = 171{\textstyle{9 \over {11}}}^\circ \]

As \[1^\circ = 60\min \],so,

\[\begin{array}{l}D.M. = 171^\circ + {\textstyle{9 \over {11}}}^\circ \\ = 171^\circ + ({\textstyle{9 \over {11}}}) \times 60'\\ = 171^\circ + ({\textstyle{{540} \over {11}}})'\\ = 171^\circ + 49{\textstyle{1 \over {11}}}'\\ = 171^\circ + 49' + {\textstyle{1 \over {11}}}'\end{array}\]

As \[1\min = 60\sec \],so,

\[\begin{array}{l}D.M. = 171^\circ + 49' + {\textstyle{1 \over {11}}} \times 60''\\ = 171^\circ + 49' + {\textstyle{{60} \over {11}}}''\\ = 171^\circ + 49' + 5.45''\end{array}\]

Hence, \[D.M.\]\[ = 171^\circ 49'5.45''\] which is approximately \[171^\circ 49'6''\].

So, 3 Radians is 171 degrees 49 minutes and 6 seconds.

2. Convert 25° into Radians.

Ans: Given D.M.=25°.

\[R.M = \dfrac{\pi }{{{{180}^ \circ }}} \times D.M.\]

\[\begin{array}{l} = \dfrac{\pi }{{180^\circ }} \times 25^\circ \\ = \dfrac{{25\pi }}{{180}}\\ = \dfrac{{25 \times {\textstyle{{22} \over 7}}}}{{180}}\\ = \dfrac{{25 \times 22}}{{180 \times 7}}\\ = \dfrac{{550}}{{1260}}\\ = 0.436rad\end{array}\]

So, 25° is 0.436 rad.

3. Find the angle in radians and degrees through which a pendulum swings if its length is 75 cm and the tip describes an arc of length 15 cm.

Ans: Given the length of arc=l=15 cm.

Radius of arc=r=75 cm.

To find Angle subtended by arc in degrees.

As we know, \[{\rm{Angle}}\left( {{\rm{Radian\;Measure}}} \right) = {\rm{\theta }} = \dfrac{{\text{Length of arc}}}{{\text{Radius}}} = \dfrac{l}{r}\]

So, \[\theta = \dfrac{{15cm}}{{75cm}} = \dfrac{1}{5}rad\]

Also, \[D.M = \dfrac{{180^\circ }}{\pi } \times R.M.\]

\[ \Rightarrow D.M. = \dfrac{{180^\circ }}{\pi } \times \dfrac{1}{5}\]

\[ = \dfrac{{180^\circ }}{{5\pi }}\]

\[ = \dfrac{{180^\circ }}{{5 \times \dfrac{{22}}{7}}}\]

\[ = \dfrac{{180^\circ \times 7}}{{5 \times 22}}\]

\[ = \dfrac{{1260}}{{110}}\]

\[ = 114{\textstyle{6 \over {11}}}^\circ \]

\[\begin{array}{l} = 114^\circ + ({\textstyle{6 \over {11}}} \times 60)'\\ = 114^\circ + ({\textstyle{{360} \over {11}}})'\\ = 114^\circ + 32' + ({\textstyle{8 \over {11}}})'\\ = 114^\circ + 32' + ({\textstyle{8 \over {11}}} \times 60)''\\ = 114^\circ + 32' + ({\textstyle{{480} \over {11}}})''\\ = 114^\circ + 32' + 43.63''\\ = 114^\circ 32'43.63''\\ \simeq 114^\circ 32'44''\end{array}\]

So, the Radian Measure is \[\dfrac{1}{5}\]rad and Degree Measure is \[114^\circ 32'44''\].

Key Features

• Radian Measure and Real numbers are equivalent quantities.

• The Conversion formulas for Radian Measure and Degree Measure are:\[R.M = \dfrac{\pi }{{{{180}^ \circ }}} \times D.M.\] and\[D.M = \dfrac{{180^\circ }}{\pi } \times R.M.\]

• \[2\pi rad = {360^ \circ }\].

Practice Questions

Q1. Convert into Radian Measure: \[ - 15^\circ \].

Answer: \[-\dfrac{\pi}{12}\]

Q2. Convert into Degree Measure: \[4\pi\] rad.

Answer: \[720^\circ\]