Why The Perpendicular To A Tangent Always Passes Through The Center With Proof And Examples
Perpendicular lines are the two distinct lines that intersect at each other at $90^{\circ}$. Have you noticed anything common between the joining corners of your walls or the letter "L"? They are the straight lines known as perpendicular lines that meet each other at a specific angle - the right angle. We say that a line is perpendicular to another line if the two lines meet at an angle of $90^{\circ}$. The word "tangent" means "to touch". The Latin word for the same is "tangere". In general, we can say that the line that intersects the circle exactly at one point on its circumference and never enters the circle's interior is a tangent. A circle can have many tangents. They are perpendicular to the radius. In this article, we will see the proof of the perpendicular at the point of contact to the tangent.
What is Perpendicular?
A perpendicular is a straight line that makes an angle of $90^{\circ}$ with another line. $90^{\circ}$ is also called a right angle and is marked by a little square between two perpendicular lines as shown in the figure. Here, the two lines intersect at a right angle, and hence, are said to be perpendicular to each other.
Perpendicular line
What is a Tangent?
A tangent is a line that just barely touches a curve at a single point, without actually intersecting the curve. In other words, it's a line that's coincident to the curve at that particular point. The point where it touches the edge of the circle is called the point of tangency.
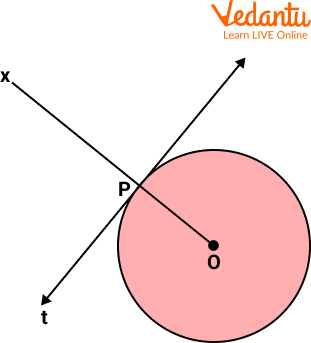
Line t is tangent to the circle in the figure.
Prove the Perpendicular at the Point of Contact to the Tangent that Passes Through the Centre of the Circle
The perpendicular at the point of contact to the tangent to a circle passes via the centre of the circle. This can be proven by considering the tangent to the circle as a line that is perpendicular to the radius at the point of contact. Therefore, the perpendicular bisector of the radius at the point of contact passes through the centre of the circle.
Construction
Let's draw a tangent PQ to a circle as shown below.
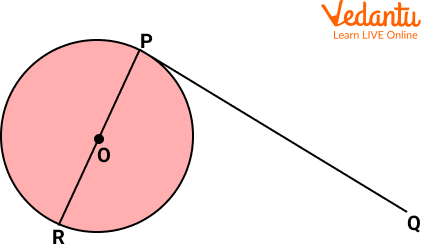
Example
As we know, a tangent at any point of a circle is perpendicular to the radius through the point of contact.
At the point of contact P, RP is perpendicular to the tangent PQ.
We also know that the radius or diameter will always pass through the centre of the circle.
Therefore, PR passes through the centre O.
Hence it is proved that perpendicular PR of tangent PQ passes through centre O.
Solved Examples
Q 1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. What will be the radius of the circle?
Ans: So first of all we are going to draw the figure based on the information we have.
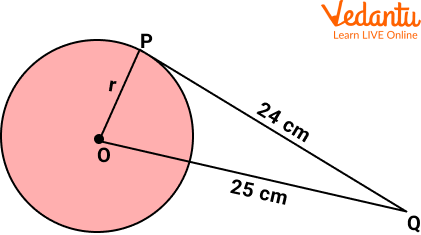
Tangent PQ
A tangent at any point of a circle is perpendicular to the radius at the point of contact.
Therefore, OPQ is a right-angled triangle.
By Pythagoras theorem,
$O Q^2=O P^2+P Q^2$
$25^2=r^2+24^2$
$r^2=25^2-24^2$
$r^2=625-576$
$r^2=49$
$r=\pm 7$
Radius cannot be a negative value, hence, $r=7 \mathrm{~cm}$.
Q 2. What will be the length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm?
Ans: Let $\mathrm{O}$ be the circle's centre. $\mathrm{OA}$ is the radius of the circle and $\mathrm{OP}$ is $8 \mathrm{~cm}$ According to question, we have
$\angle \mathrm{OAP}=90^{\circ}$
So, by Pythagoras theorem, we get
$\mathrm{OP}^2=\mathrm{OA}^2+\mathrm{AP}^2$
$\Rightarrow \mathrm{AP}^2=\mathrm{OP}^2-\mathrm{OA}^2$
$\Rightarrow \mathrm{AP}^2=8^2-6^2$
$\Rightarrow \mathrm{AP}^2=64-36$
$\Rightarrow \mathrm{AP}^2=28$
$\Rightarrow \mathrm{AP}=2 \sqrt{7} \mathrm{~cm}$
Therefore, the length of the tangent will become $2 \sqrt{7} \mathrm{~cm}$.
Practice Questions
Q 1. Perpendicular lines ___________
will never intersect
intersect to form right angles
are curved lines
are not coplanar
Ans: Intersect to form right angles
Q 2. If the length of the tangent line is 4 cm drawn from any point, 10 cm away from the centre of the circle, then what will be the radius of that circle?
Ans: $\sqrt{84} \mathrm{~cm}$
Summary
A perpendicular makes a 90 degree angle. A tangent touches the circle at one point only which is called the tangency point.The perpendicular at the point of contact to the tangent to a circle passes through the centre of the circle. This can be proven by considering the tangent to the circle as a line that is perpendicular to the radius at the point of contact. Therefore, the perpendicular bisector of the radius at the point of contact passes through the centre of the circle.
FAQs on Perpendicular At Contact Point To Tangent Passes Through Circle Center
1. What is the theorem about the perpendicular at the point of contact to a tangent of a circle?
The perpendicular at the point of contact to a tangent of a circle passes through the centre of the circle. This means that if a tangent touches a circle at point P, then the line drawn from P perpendicular to the tangent will pass through the centre O of the circle.
- Let O be the centre of the circle.
- Let PT be the tangent at point P.
- Then OP ⟂ PT.
2. Why does the perpendicular at the point of contact pass through the centre?
The perpendicular at the point of contact passes through the centre because the radius drawn to the point of tangency is always perpendicular to the tangent. Since all radii of a circle are equal, the shortest distance from the centre to the tangent occurs at the point of contact.
- The radius OP is fixed in length.
- A tangent touches the circle at exactly one point.
- The shortest distance from O to the tangent line is the perpendicular.
3. How do you prove that the radius is perpendicular to the tangent at the point of contact?
To prove this theorem, show that the radius to the point of contact forms a 90° angle with the tangent.
- Let PT be the tangent at point P of a circle with centre O.
- Assume OP is not perpendicular to PT.
- Then a shorter distance from O to PT can be drawn.
- This contradicts the fact that OP is the radius and the shortest distance to the tangent.
4. What is the angle between the tangent and the radius at the point of contact?
The angle between the tangent and the radius at the point of contact is 90°. If OP is the radius and PT is the tangent at point P, then:
- ∠OPT = 90°
5. Does the perpendicular from the centre to a tangent always meet it at the point of contact?
Yes, the perpendicular from the centre to a tangent always meets it exactly at the point of contact. Since the radius drawn to the tangent point is perpendicular to the tangent line, that perpendicular determines the touching point.
- Let O be the centre.
- Draw a perpendicular from O to the tangent.
- The foot of the perpendicular is the point of tangency.
6. How is this theorem used in coordinate geometry?
In coordinate geometry, this theorem is used by applying the condition that the slope of the radius × slope of the tangent = −1. Since the radius is perpendicular to the tangent at the point of contact:
- If slope of radius = m₁
- Then slope of tangent = m₂
- m₁ × m₂ = −1
7. Can you give an example using numbers for this theorem?
Yes, for example, consider a circle with centre O(0, 0) and a tangent at point P(3, 4). The radius OP has slope:
- m₁ = (4 − 0)/(3 − 0) = 4/3
- m₁ × m₂ = −1
- (4/3)m₂ = −1
- m₂ = −3/4
8. What is the difference between a secant and a tangent in a circle?
A tangent touches the circle at exactly one point, while a secant intersects the circle at two points. Key differences include:
- Tangent: One point of contact.
- Secant: Two points of intersection.
- The radius is perpendicular to the tangent at the contact point.
- No such perpendicular property applies to a secant.
9. How do you find the centre of a circle using tangents?
You can find the centre by drawing perpendicular lines at the points of contact of tangents. Steps:
- Draw tangents at two different points on the circle.
- At each point of contact, draw a perpendicular to the tangent.
- The two perpendicular lines intersect at the centre of the circle.
10. What are common mistakes when applying the perpendicular to tangent theorem?
A common mistake is assuming any line from the centre to the tangent is perpendicular, instead of only the radius drawn to the point of contact. Other errors include:
- Confusing tangent with secant.
- Not verifying the exact point of contact.
- Forgetting that perpendicular slopes satisfy m₁ × m₂ = −1.
