What is PEMDAS?
It is always easier to deal with a single operation like only addition, subtraction, multiplication, or division. When a couple of them or all of the operations are involved at once, it becomes difficult to judge which operation must be fulfilled first.
In such a situation the PEMDAS rule comes into the picture.
Before diving into what is PEMDAS, the PEMDAS full form, situations where this is used and all other million questions in your mind, it’s important to un-wrap this concept part by part. Only then you will be able to answer the PEMDAS examples. Let’s jump right in!
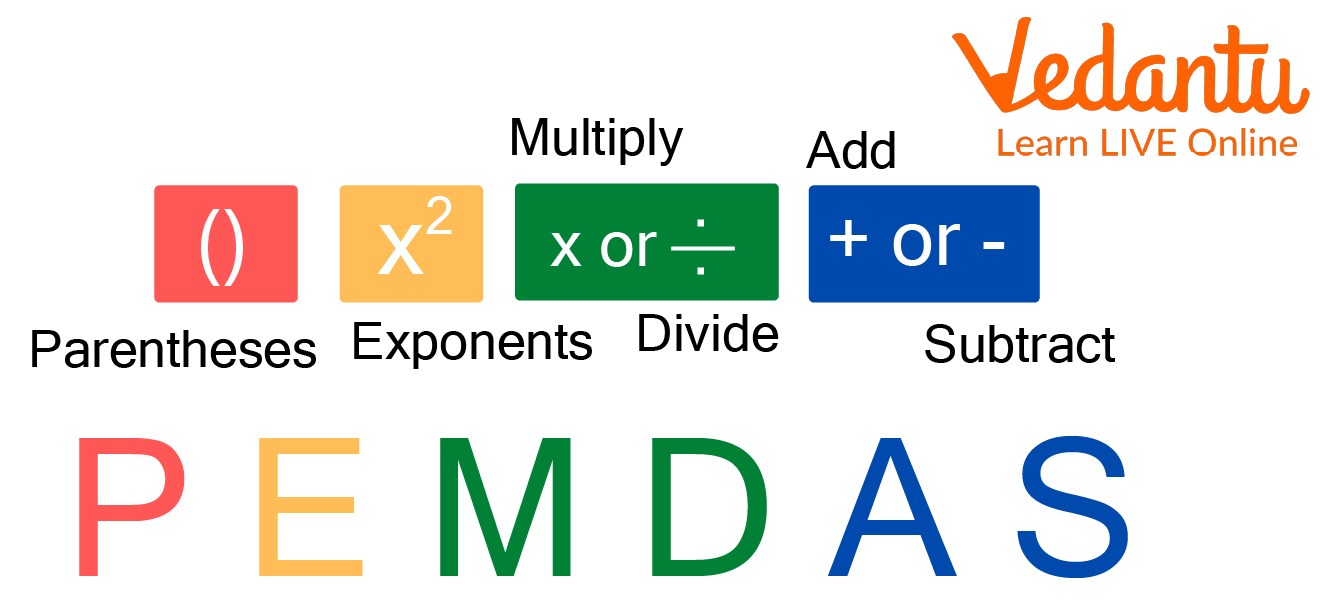
What is PEMDAS?
What does PEMDAS Stand for?
PEMDAS is nothing but an abbreviation for the parts and order of different operations that have to be dealt with when multiple operations are involved in the given equation. PEMDAS full form helps us to remember the sequence of the operations that have to be performed.
If that is super complex to understand, it is the short form for the following parts:
P for Parentheses (or Brackets)
E for Exponents (squares and roots are called so)
M for Multiplication
D for Division
A for Addition
S for Subtraction
Why PEMDAS?
As remembering a whole list of operations is a lot more of a task than remembering this weird-sounding word! More than that, mathematics is a subject of organization and logic, so the PEMDAS rule proves just that.
This rule helps us understand the priorities of operations.
When given a list of things to do, we tend to panic and lose track of what to do first and what comes next. The PEMDAS method prevents this confusion and helps you get through the list of operations with ease.
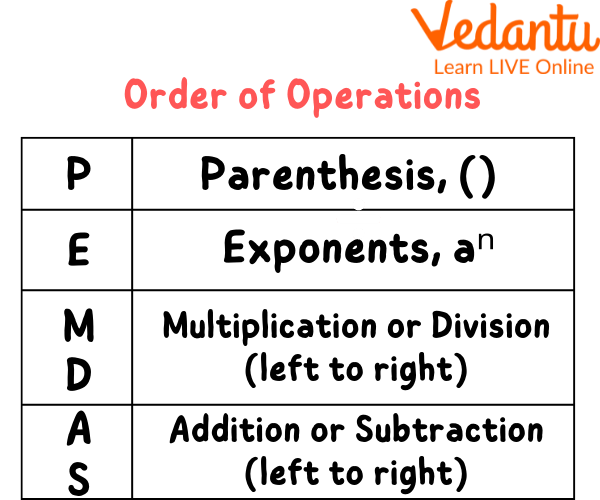
Order of Operations According to The PEMDAS Rule
How is The PEMDAS Method Carried Out?
The full form of PEMDAS says pretty much everything about this method. Anyways, let’s brush through the steps one by one.
Step 1- Deal with the parentheses! Any operation within the brackets or parentheses must be solved first. Irrespective of it being addition, subtraction, multiplication, or division.
Step 2- Little numbers are the next big problem. Exponents! Square and Cube the given powers wherever necessary to jump to the next step.
Step 3- Always remember to start from the left and solve whatever comes first, be it multiplication or division.
Step 4- Same rule of left to the right applies here too! Solve whatever comes first, be it addition or subtraction.
Solved Examples
PEMDAS Examples with Answers
Q1. Solve the following equation using the PEMDAS method
$3 \times 6(7-4)-2^{2}+5 \times 6$
Ans: Solving what's given in the parentheses we get $3 \times 6(3)-2^{2}+5 \times 6$
Solving exponents given in the equation
$3 \times 6 \times 3-4+5 \times 6$
First we solve the multiplication and division from left to right $54-4+30$
Next, we solve the addition and subtraction from left to right
$54 - 4 + 30 = 80$
Final answer is 80
Q2. Solve the following equation using the PEMDAS method
$6^{2} \times(32-29)$
Ans: Solving what's given in the parentheses, we get $=6^{2} \times 3$
Solving exponents given in the equation $=36 \times 3$
Next, we solve the multiplication
$=108$
Final answer is 108
Q3. Solve the following equation using the PEMDAS method
$11^{2}-3(41+0-39)$
Ans: Solving what's given in the parentheses, we get
$=11^{2}-3 \times 2$
Solving the exponents in the equation
= 121 - 6
Now, subtracting 121 - 6 =115
Final answer is 115.
Q4. Solve the following equation using the PEMDAS method
= 24 × 4(65-23)
Ans: Solving what’s given in the parentheses
= 24 × 4 × 42
Now, multiplying we get 4032
Final answer is 4032.
Practice Problems
Q1. Solve the following equation using the PEMDAS method 4+3[8-2(6-3)]÷2
Ans: 39
Q2. Solve the following equation using the PEMDAS method 18÷(8-2×3)
Ans: 9
Q3. Solve the following equation using the PEMDAS method 20+34(45÷5)
Ans: 326
Q4. Solve the following equation using the PEMDAS method 10×5(20÷4)
Ans: 250
Q5. Solve the following equation using the PEMDAS method 8×5(88÷88)
Ans: 40
Summary
The PEMDAS rule gives the order of operations that has to be followed when dealing with a bunch of different operations. It stands for the following operations in the given order, P for parentheses, E for exponents, M for multiplication, D for division, A for addition, and S for Subtraction.
It is also necessary to remember another important rule of following from left to right i.e. operations on the left of the equation have to be followed before getting to the right of the equation. PEMDAS makes operations easier to perform. By practicing a few PEMDAS examples with answers, it becomes much easier.
FAQs on PEMDAS Rule
1. Do BODMAS and PEMDAS have the same set of rules?
No, they don’t have the same set of rules. Both have different rules.
BODMAS | PEMDAS |
BODMAS abbreviates Brackets, Order, Division, Multiplication, Addition, and subtraction. | PEMDAS's full form is Parentheses, Exponents, multiplication, division, addition, and subtraction. |
In BODMAS there is no left-to-right rule. | PEMDAS rule follows the left-to-right rule. |
Exponents have no place in the BODMAS rule | Exponents are given enough attention in the PEMDAS method and are solved before getting to multiplication and division. |
2. Do you multiply or divide first Pemdas?
According to the order of operations, you should do addition and subtraction last and multiply and division first, proceeding from left to right. Divide and multiply from left to right as you continue.
In the PEMDAS rule, Multiplication comes before Division, although the two are completed in a single step from left to right. In the same step, both addition and subtraction are performed. It’s important to stick to the rule of solving operations from left to right when solving the PEMDAS examples.
3. Who invented the PEMDAS rule?
Nobody Invented PEMDAS. People gradually discovered the best techniques and practices which later became standards. A section of an algebra textbook for the military academy published in 1838, written for military engineers rather than academic mathematicians or elementary school students, has the first explicit reference to the PEMDAS rule in Dutch.