Maths Project

Mathematics is a word that most of the students in their early grade until then and now.

The early graders normally fear the word "Mathematics". But in reality, maths is a subject full of logic and proof.

This is no longer primary to teach the students in the 21st century. Including Mathematics Project in the upper primary stage aids students in picturing the fundamental concepts, principles, theorems, and the underlying procedure occupied in solving them. Mathematics is a word that is feared by the largest of the students in their early grades.

Following are some of the advantages of Maths projects in our schools:

1. While traditional learning is not much suggested to solve the maths problems, it is recommended to the teachers and board to grant maths education in a more rational and challenging way through project works.

2. It has been seen that rote learning is not effective in the long term. Maths related projects work not only to help in improving the problem-solving ability but also will be able to learn it in a better way for their lifetime.

3. These projects help the students to improve their planning and critical thinking ability as they employ “habit of thinking and mind skills”.

4. Including this concept in the curriculum will also help improve the reasoning skills of the student.

5. Remember when you try to learn something relating to the real world you understand it better. Similarly, when you try to learn a concept with more examples and relate it to the real world the concept gets deeper into your mind and retains forever and ever. Henceforth, it is always good to do a project on the concept you have understood.

Project 1 

Probability:

Probability is such a native part of your life that you rarely think about it. Though, every time you use a word like “might,” “may,” “undoubtedly,” “without fail,” or “maybe,” you can see and even a probability that an event will occur.

Scientists and great mathematicians like to express probability more accurately. For example, if you toss a coin in the air, the probability (P) that it will land heads or tails.

Materials Required:

1. A book and a pencil.

2. Four coins.

Procedure: 

Using a paper and pencil, draw circles with an “H” or a “T” in the centre of the paper to illustrate the different results when you toss these three coins.

Using the circles that you drew as mentioned above, express the following:

• The probability of getting three heads while tossing the coins.

• The probability of getting three tails while tossing the coins.

• The probability of getting one head and three tails while tossing the coins.

• The probability of getting one tail and three heads while tossing the coins.

Hint: There are eight distinctly different possibilities so make sure you haven’t left any of them out.

Try tossing three coins 16 times and writing down the outcomes. Are the probabilities roughly equal as you calculated in step 2? Try tossing three coins 24 times. Are the probabilities any closer?

Project 2 

Pythagoras Theorem:

This theorem states that the square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.

(Image will be Uploaded Soon)

Materials Required:

1. Colour papers

2. Ruler and sketches

Procedure:

Make a right angle Triangle, of 3cm, 4cm and 5cm as shown 3cm 5cm.

Make 3 square sheets of 3 * 3 cm, 4 * 4 cm, 5 * 5 cm.

Fix these square sheets to the sides of the triangle.

Make the square sheets into 3 * 3 cm such that 9 squares of equal length

Similarly, repeat the same thing with the remaining square sets. 4cm

By this work, we can prove the above-said theorem.

(Image will be Uploaded Soon)

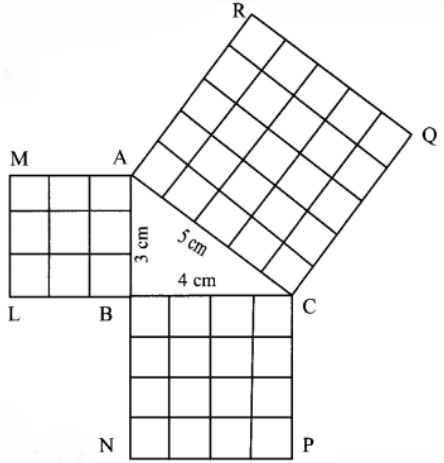
In the above work, we have considered a = 3cm, b = 4cm and c = 5cm.

Henceforth, 3 square + 4 square = 5 square. 

• 3 * 3 + 4 * 4 = 5 * 5 

• 9 + 16 = 25 

• 25 = 25

Hence the theorem is proved. 

Assessment: 

1. Geometry Map Project:

Angles, Lines, and Triangles: Your assignment is to design a map that includes several distinct kinds of lines, angles, and triangles. Your map can be of a town, your neighbourhood or a made-up place of your own. It must, however, incorporate the following: 2 sets of streets that are parallel Two sets of streets that are perpendicular One street that intersects another street to form an obtuse angle.

2. Restaurant Menu Project: 

Create a menu for a themed restaurant. The student will write word problems using their menu. It can be a very fundamental element, just adding prices of different items, to more complex problems, like finding the cost of a meal for you and a friend plus tax or figuring the cost of the meal for grandma with her senior discount of 10%. The criteria for each of the following items in the menu are as follows: 4 different types of appetizers, 4 different types of beverages and 4 main dishes.

3. Compare Two Fractions:

Two proper fractions are given to you with different denominators (show how to write these fractions as decimal numbers and as a percentage. Compare both the fractions using an appropriate mathematical symbol.) Be sure to explain what you are thinking!

4. Supplementary and Complementary Angles:

Label and highlight the given angles from 6 different pictures. Select six of the following angles: acute angle, obtuse angle, straight, right angle, supplementary angles, and complementary angle. Then measure the acute angle, obtuse angle, supplementary angle, and complementary angles, and write their measures inside the interior of each angle.

5. Design Your Dream House: 

Draw a 2D version of how you want the front of your house to look like. Must include four windows, and two doors. All lines must be drawn with the help of a ruler and must be in centimetres. Students must then determine the perimeter and area of each window and the door. You must also do the same for the front of the house such that the perimeter and the area. Then you must convert these measurements to millimetres. Each dimension must be written in a typical drafting fashion. Houses must be uniformly coloured, and students may add additional features.

6. Mathematics Article: 

Draft an article about mathematics, which may include a mathematician. Write 2 important things you learned from the article. At least one-page minimum. Note, write the summary in your own words!

Maths Project assists pupils in developing their critical thinking and reasoning skills. Most schools provide exhibits for classes 5, 6, 7, 8, 9, and 10, where students may display their unique ideas and project work using mathematical models, allowing them to study the topic in a creative way.

There's an ancient adage that goes, "Tell me, and I'll forget; show me, and I'll remember; involve me, and I'll comprehend." Confucius, a Chinese philosopher, said

Today's youth expects an interactive learning paradigm that will keep them engaged and help them absorb the facts quickly. Previously, the primary instrument used by schools to impart instruction was:

• Reading,

• writing, 

• testing, 

• repeating

This is no longer necessary to teach pupils in the twenty-first century. This is why the CBSE board of governors has approved a project-based training and learning programme for pupils. Incorporating a Maths project into the CBSE and ICSE curricula has aided millions of students in their professional pursuits.

Benefits of Maths Project Work:

Incorporating a Maths Project into the upper elementary stage assists children with conceptualising the fundamental ideas, theorems, and principles, as well as the underlying method required in solving them. Mathematics is a word that most pupils in their early grades despise. Some pupils utilise arithmetic techniques to solve problems, while others study hard. Maths is a topic that is full of reasoning and proof. The following are some of the benefits of maths projects in schools:

• While rote learning is not suggested for solving arithmetic problems, instructors and the board are encouraged to deliver maths education in a more sensible and demanding manner through project work.

• Role-learning or memorization is ineffective for long-term memory. Maths-related project work not only improves problem-solving abilities but also allows students to learn in a rewarding method that will last a lifetime.

• Maths projects assist pupils to enhance their planning and critical thinking abilities by utilising "habit of thinking and cognitive skills." Incorporating maths projects into the curriculum will also assist students to enhance their thinking abilities.

• Students are required to showcase what they have made for their projects in front of the class. This, in turn, assists students in improving their communication and presenting abilities, which will serve them well in their professional careers.

Keeping all of these benefits in mind for the Maths project will aid in producing a memorable learning experience for the pupils.

Maths Project Ideas

Maths Project enables students to put their ideas into practice and get real-world experience. It will assist students in developing interpersonal skills and cognitive ability, as well as increasing their degree of confidence in the topic. Let's look at several maths models here;

Real-world Mathematical Number System

• Area and perimeter of various sorts of forms and shapes

• Angle Types

• Probability and statistics 

• Algebraic Equations and Quadratic 

• Pythagoras' Theorem

• Conic Sections

These are the few general themes for which students can develop a model.

Class 10 Maths Model

For pupils in class 10, we've included some project ideas for maths that are related to their curriculum and can be simply reproduced.

Surface area and volume of a Cube and a Cuboid: 

Students in Grade 10 must be able to compute the surface areas and volumes of specified 3D objects such as a cube, a cuboid, and so on. Try to recognise the 3D forms around you and investigate how we can calculate their surface area and volume.

Areas of two comparable triangles are compared:

The notion of similar triangles is simple to memorise; however, understanding the link between the areas of two similar triangles using their sides is essential.

Finding the angles using trigonometric ratios: 

As we all know, trigonometry can be used to locate the missing sides or angles of a right triangle. More similar situations will be practised with the assistance of a maths project model on trigonometry. The use of trigonometric ratios will aid in determining the needed parameters.

The following are the mean values of the provided data:

In general, we deal with many numbers in our daily lives, and it is often necessary to know the average of these figures, such as the average time to complete a given activity. In this scenario, the idea of mean values is the most efficient way to get the desired outcome.

Probability of random experiments: 

This probability maths project aids in understanding different types of random experiments and determining the probabilities of occurrences related to them. For example, in the experiment of tossing a coin three times, receiving exactly two heads.

Model for 9th Grade Maths Project

Students in Class 9 can utilise these project ideas to construct maths models that are aligned with their curriculum. Try out these 9th grade Math project ideas and have fun while learning.

• Numbers are represented in a number line.

• In Coordinate Geometry, the Cartesian Plane is used.

• Geometry Shapes Types of Triangles Euclid's Geometry Model.

Maths Project Ideas for Class 8 

Secondary students in Class 8 can create some of the greatest functional models based on the following topics:

• Creating various types of quadrilaterals

• Number line representation of rational numbers

• Data grouping, organisation, and display using charts and graphs.

• Profit and loss for commodities, as well as the discovery of simple interest

• Having fun with numbers

• Linear graphs (use matchsticks to represent)

• 3D Object Visualisation

7th Grade Maths Project

With the aid of practical models, students in Class 7 may easily grasp Mathematics and related principles. They can acquire several project ideas from here to make such models. These models will assist students in visualising topics and developing their confidence in any given area.

Here are the subjects on which students will base their projects.

• Integer data types (positive and negative)

• Fractional Forms (Proper and Improper fractions)

• In two-dimensional space, what are lines and angles?

• Triangle Shapes (Scalene, Isosceles and Equilateral)

• Quantity Comparison

• Symmetry

• Imagining Solid Shapes

Maths Project for 6th Grade

When pupils advance from class 5th to class 6th, their educational level rises. They will be introduced to numerous new topics that they did not study in elementary school.

As a result, doing maths projects based on various topics and properly understanding them will be quite fascinating for children.

• Knowing and comparing various figures

• Whole-number patterns

• Defining a Point, a Line, and an Angle (Basic geometry)

• Line models of parallel and perpendicular lines

• What exactly are decimals and fractions?

• Matchstick Patterns in Algebra

• Formal symmetry

Mathematical Working Models for Exhibits

Several mathematical projects may be made in school displays, such as:

Calculator: The calculator is constructed of cardboard and has four holes, with the first, third, and fourth holes containing moveable numbers and the second hole containing all the symbols depending on the operations performed: addition, subtraction, division, and multiplication. In this manner, we might construct a man-made calculator and assess the abilities of the exhibition's attendees.

Here are some more nice ideas for developing workable models based on mathematical concepts:

• Construct a school project in which each building is represented by a distinct form. For example, the school's roof will be shaped like a triangle.

• Create a model using LED lights that are based on trigonometric ratios (Sine, Cosine, and Tangent).

• Make a "height and distance" model out of cardboard, paper, pulleys, threads, and other materials.

• Using LED lights, match the following model for square and cube numbers.

• A model that represents the centroid of several sorts of triangles (Acute, Obtuse and right triangle)

• Make a model that depicts the many sections of a circle (radius, diameter, the centre of the circle, chord, sector, arc, etc.)

• Geometrical forms in three dimensions

Conclusion

CBSE has included maths projects in its formative and summative classes, and the percentage of marks assigned to the projects ranges from 10% to 15%. The project might take the shape of high-level thinking skills questions or case studies. The class teacher may also reach the pupils through an open book assessment test at times.

The benefits underlie the strategy of accessing their children through maths projects and out-of-school learning. This assists students in making real-life decisions and acquiring mathematical information in a more holistic manner, which will benefit them in their career and professional lives.

We approach making students learn through interactive sessions, and films allow students to study in a dynamic manner.